How long does it take until economic agents converge to an equilibrium? By studying the complexity of the problem of computing a mixed Nash equilibrium in a game, we provide evidence that there are games in which convergence to such an equilibrium takes prohibitively long. Traditionally, computational problems fall into two classes: those that have a polynomial-time algorithm and those that are NP-hard. However, the concept of NP-hardness cannot be applied to the rare problems where “every instance has a solution”—for example, in the case of games Nash’s theorem asserts that every game has a mixed equilibrium (now known as the Nash equilibrium, in honor of that result). We show that finding a Nash equilibrium is complete for a class of problems called PPAD, containing several other known hard problems; all problems in PPAD share the same style of proof that every instance has a solution.
1. Introduction
In a recent CACM article, Shoham22 reminds us of the long relationship between Game Theory and Computer Science, going back to John von Neumann at Princeton in the 1940s, and how this connection became stronger and more crucial in the past decade due to the advent of the Internet: Strategic behavior became relevant to the design of computer systems, while much economic activity now takes place on computational platforms.
Game Theory is about the strategic behavior of rational agents. It studies games, thought experiments modeling various situations of conflict. One commonly studied model aims to capture two players interacting in a single round. For example, the well-known school yard game of rock-paper-scissors can be described by the mathematical game shown in Figure 1. There are two players, one choosing a row and one choosing a column; the choices of a player are his/her actions. Once the two players choose, simultaneously, an action, they receive the corresponding payoffs shown in the table: The first number denotes the payoff of Row, the second that of Column. Notice that each of these pairs of numbers sum to zero in the case of Figure 1; such games are called zero-sum games. Three other well-known games, called chicken, prisoner’s dilemma, and penalty shot game, respectively, are shown in Figure 2; the penalty shot game is zero-sum, but the other two are not. All these games have two players; Game Theory studies games with many players, but these are harder to display.a
The purpose of games is to help us understand economic behavior by predicting how players will act in each particular game. The predictions game theorists make about player behavior are called equilibria. One such prediction is the pure Nash equilibrium: Each player chooses an action that is a “best response” to the other player’s choice—i.e., it is the highest payoff, for the player, in the line, row or column, chosen by the other player. In the game of chicken in Figure 2, a pure Nash equilibrium is when one player chooses “dare” and the other chooses “chicken.” In the prisoner’s dilemma, the only pure Nash equilibrium is when both players choose “defect.”
Unfortunately, not all games have a pure Nash equilibrium. For example, it is easy to see that the rock-paper-scissors game in Figure 1 has none. This lack of universality is an important defect of the concept of pure Nash equilibrium as a predictor of behavior. But the rock-paper-scissors game does have a more sophisticated kind of equilibrium, called a mixed Nash equilibrium—and in fact one that is familiar to all who have played this game: both players pick an action uniformly at random. That is, a mixed Nash equilibrium is a probabilistic distribution on the set of actions of each player. Each of the distributions should have the property that it is a best response to the other distributions; this means that each action assigned positive probability is among the actions that are best responses, in expectation, to the distribution(s) chosen by the opponent(s).
In 1950, John Nash proved that all games have a mixed Nash equilibrium.19 That is, in any game, distributions over the players’ actions exist such that each is a best response to what everybody else is doing. This important—and far from obvious—universality theorem established the mixed Nash equilibrium as Game Theory’s central equilibrium concept, the baseline and gold standard against which all subsequent refinements and competing equilibrium concepts were judged.
Universality is a desirable attribute for an equilibrium concept. Of course, such a concept must also be natural and credible as a prediction of behavior by a group of agents—for example, pure Nash seems preferable to mixed Nash, in games that do have a pure Nash equilibrium. But there is a third important desideratum on equilibrium concepts, of a computational nature: An equilibrium concept should be efficiently computable if it is to be taken seriously as a prediction of what a group of agents will do. Because, if computing a particular kind of equilibrium is an intractable problem, of the kind that take lifetimes of the universe to solve on the world’s fastest computers, it is ludicrous to expect that it can be arrived at in real life. This consideration suggests the following important question: Is there an efficient algorithm for computing a mixed Nash equilibrium? In this article, we report on results that indicate that the answer is negative—our own work 5, 7, 8, 13 obtained this for games with three or more players, and shortly afterwards, the papers2, 3 extended this—unexpectedly—to the important case of two-player games.
Ever since Nash’s paper was published in 1950, many researchers have sought algorithms for finding mixed Nash equilibria—that is, for solving the computational problem which we will call NASH in this paper. If a game is zero-sum, like the rock-paper-scissors game, then it follows from the work of John von Neumann in the 1920s that NASH can be formulated in terms of linear programming (a subject identified by George Dantzig in the 1940s); linear programs can be solved efficiently (even though we only realized this in the 1970s). But what about games that are not zero-sum? Several algorithms have been proposed over the past half century, but all of them are either of unknown complexity, or known to require, in the worst case, exponential time.
During the same decades that these concepts were being explored by game theorists, Computer Science theorists were busy developing, independently, a theory of algorithms and complexity addressing precisely the kind of problem raised in the last two paragraphs: Given a computational problem, can it be solved by an efficient algorithm? For many common computational tasks (such as finding a solution of a set of linear equations) there is a polynomial-time algorithm that solves them—this class of problems is called P. For other such problems, such as finding a truth assignment that satisfies a set of Boolean clauses (a problem known as SAT), or the traveling salesman problem, no such algorithm could be found after many attempts. Many of these problems can be proved NP-complete, meaning they cannot be solved efficiently unless P = NP—an event considered very unlikely.11
From the previous discussion of failed attempts to develop an efficient algorithm for NASH, one might be tempted to suppose that this problem too is NP-complete. But the situation is not that simple. NASH is unlike any NP-complete problem because, by Nash’s theorem, it is guaranteed to always have a solution. In contrast, NP-complete problems like SAT draw their intractability from the possibility that a solution might not exist—this possibility is used heavily in the NP-completeness proof.b See Figure 3 for an argument (due to Nimrod Megiddo) why it is very unlikely that NP-completeness can characterize the complexity of NASH. (Note however that if one seeks a Nash equilibrium with additional properties—such as the one that maximizes the sum of player utilities, or one that uses a given strategy with positive probability—then the problem does become NP-complete.4, 12)
Since NP-completeness is not an option, to understand the complexity of NASH one must essentially start all over in the path that led us to NP-completeness: We must define a class of problems which contains, along with NASH, some other well-known hard problems, and then prove that NASH is complete for that class. Indeed, in this paper we describe a proof that NASH is PPAD-complete, where PPAD is a subclass of NP that contains several important problems that are suspected to be hard, including NASH.
1.1. Problem statement: Nash and approximate Nash equilibria
A game in normal form has some number k of players, and for each player p (p
{1, …, k}) a finite set Sp of pure actions or strategies. The set S of pure strategy profiles is the Cartesian product of the Sp‘s. Thus, a pure strategy profile represents a choice, for each player, of one of his actions. Finally, for each player p and s
S the game will specify a payoff or utility ups≥0, which is the value of the outcome to player p when all the players (including p) choose the strategies in s. In a Nash equilibrium, players choose probability distributions over their Sp‘s, called mixed strategies, so that no player can deviate from his mixed strategy and improve on his expected payoff; see Figure 4 for details.
For two-player games there always exists a Nash equilibrium in which the probabilities assigned to the various strategies of the players are rational numbers—assuming the utilities are also rational. So, it is clear how to write down such a solution of a two-player game. However, as pointed out in Nash’s original paper, when there are more than two players, there may be only irrational solutions. In this general situation, the problem of computing a Nash equilibrium has to deal with issues of numerical accuracy. Thus, we introduce next the concept of approximate Nash equilibrium.
If Nash equilibrium means “no incentive to deviate,” then approximate Nash equilibrium stands for “low incentive to deviate.” Specifically, if ε is a small positive quantity, we can define an ε-Nash equilibrium as a profile of mixed strategies where any player can improve his expected payoff by at most ε by switching to another strategy. Figure 4 gives a precise definition, and shows how the problem reduces to solving a set of algebraic inequalities. Our focus on approximate solutions is analogous to the simpler problem of polynomial root-finding. Suppose that we are given a polynomial f with a single variable, and we have to find a real root, a real number r satisfying f(r) = 0. In general, a solution to this problem (the number r) cannot be written down as a fraction, so we should really be asking for some sort of numerical approximation to r (for example, computing a rational number r such that | f (r)| ≤ ε, for some small ε). If f happens to have odd degree, we can even say in advance that a solution must exist, in a further analogy with NASH. Of course, the analogy breaks down in that for root-finding we know of efficient algorithms that solve the problem, whereas for Nash equilibria we do not.
We are now ready to define the computational problem NASH: Given the description of a game (by explicitly giving the utility of each player corresponding to each strategy profile) and a rational number ε > 0, compute an ε-Nash equilibrium. This should be at least as tractable as finding an exact equilibrium, hence any hardness result for approximate equilibria carries over to exact equilibria. Note that an approximate equilibrium as defined above need not be at all close to an exact equilibrium; see Etessami and Yannakakis9 for a complexity theory of exact Nash equilibria.
2. Total Search Problems
We think of NP as the class of search problems of the form “Given an input, find a solution (which then can be easily checked) or report that none exists.” There is an asymmetry between these outcomes, in that “none exists” is not required to be easy to verify.
We call such a search problem total if the solution always exists. There are many apparently hard total search problems in NP—even though, as we argued in the introduction, they are unlikely to be NP-complete. Perhaps the best-known is Factoring, the problem of taking an integer as an input and outputting its prime factors. Nash and several other problems introduced below are also total.
A useful classification of total search problems was proposed in Papadimitriou.20 The idea is this: If a problem is total, the fact that every instance has a solution must have a mathematical proof. Unless the problem can be easily solved efficiently, in that proof there must be a “nonconstructive step.” It turns out that, for all known total search problems in the fringes of P, these nonconstructive steps are one of very few simple arguments:
- “If a graph has a node of odd degree, then it must have another.” This is the parity argument, giving rise to the class PPA.
- “If a directed graph has an unbalanced node (a vertex with different in-degree and out-degree), then it must have another.” This is the parity argument for directed graphs, giving rise to the class PPAD considered in this article. Figure 5 describes the corresponding search problems.
- “Every directed acyclic graph must have a sink.” The corresponding class is called PLS for polynomial local search.
- “If a function maps n elements to n – 1 elements, then there is a collision.” This is the pigeonhole principle, and the corresponding class is PPP.
We proceed with defining more precisely the second class in the list above.
There are two equivalent ways to define NP: First, it is the class of all search problems whose answers are verifiable in polynomial time. For example, the search problem SAT (“Given a Boolean formula in CNF, find a satisfying truth assignment, or report that none exists”) is in NP because it is easy to check whether a truth assignment satisfies a CNF. Since we know that SAT is NP-complete, we can also define NP as the class of all problems that can be reduced into instances of SAT. By “reduce” we refer to the usual form of polynomial-time reduction from search problem A to search problem B: An efficient algorithm for transforming any instance of A to an equivalent instance of B, together with an efficient algorithm for translating any solution of the instance of B back to a solution of the original instance of A.
We define the class PPAD using the second strategy. In particular, PPAD is the class of all search problems that can be reduced to the problem END OF THE LINE, defined in Figure 5. Note that, since END OF THE LINE is a total problem, so are all problems in PPAD. Proceeding now in analogy with NP, we call a problem PPAD-complete if END OF THE LINE (and therefore all problems in PPAD) can be reduced to it.
2.2. Why should we believe that PPAD contains hard problems?
In the absence of a proof that P ≠ NP we cannot hope to be sure that PPAD contains hard problems. The reason is that PPAD lies “between P and NP” in the sense that, if P=NP, then PPAD itself, as a subset of NP, will be equal to P. But even if P ≠ NP, it may still be the case that PPAD-complete problems are easy to solve. We believe that PPAD-complete problems are hard for the same reasons of computational and mathematical experience that convince us that NP-complete problems are hard (but as we mentioned, our confidence is necessarily a little weaker): PPAD contains many problems for which researchers have tried for decades to develop efficient algorithms; in the next section we introduce one such problem called BROUWER. However, END OF THE LINE itself is a pretty convincingly hard problem: How can one hope to devise an algorithm that telescopes exponentially long paths in every implicitly given graph?
3. From NASH to PPAD
Our main result is the following:
THEOREM 3.1. NASH is PPAD-complete.
In the remainder of this article we outline the main ideas of the proof; for full details see Daskalakis et al.8 We need to prove two things: First, that NASH is in PPAD, that is, it can be reduced to END OF THE LINE. Second (see Section 4), that it is complete—the reverse reduction. As it turns out, both directions are established through a computational problem inspired by a fundamental result in topology, called Brouwer’s fixed point theorem, described next.
3.1. Brouwer’s fixed point theorem
Imagine a continuous function mapping a circle (together with its interior) to itself—for example, a rotation around the center. Notice that the center is fixed, it has not moved under this function. You could flip the circle—but then all points on a diagonal would stay put. Or you could do something more elaborate: Shrink the circle, translate it (so it still lies within the original larger circle), and then rotate it. A little thought reveals that there is still at least one fixed point. Or stretch and compress the circle like a sheet of rubber any way you want and stick it on the original circle; still points will be fixed, unless of course you tear the circle—the function must be continuous. There is a topological reason why you cannot map continuously the circle on itself without leaving a point unmoved, and that’s Brouwer’s theorem.16 It states that any continuous map from a compact (that is, closed and bounded) and convex (that is, without holes) subset of the Euclidean space into itself always has a fixed point.
Brouwer’s theorem immediately suggests an interesting computational total search problem, called BROUWER: Given a continuous function from some compact and convex set to itself, find a fixed point. But of course, for a meaningful definition of BROUWER we need to first address two questions: How do we specify a continuous map from some compact and convex set to itself? And how do we deal with irrational fixed points?
First, we fix the compact and convex set to be the unit cube [0, 1]m—in the case of more general domains, for example, the circular domain discussed above, we can translate it to this setting by shrinking the circle, embedding it into the unit square, and extending the function to the whole square so that no new fixed points are introduced. We then assume that the function F is given by an efficient algorithm ΠF which, for each point x of the cube written in binary, computes F(x). We assume that F obeys a Lipschitz condition:
where d(·,·) is the Euclidean distance and K is the Lipschitz constant of F. This benign well-behavedness condition ensures that approximate fixed points can be localized by examining the value F(x) when x ranges over a discretized grid over the domain. Hence, we can deal with irrational solutions in a similar maneuver as with NASH, by only seeking approximate fixed points. In fact, we have the following strong guarantee: for any ε, there is an ε-approximate fixed point—that is, a point x such that d(F(x), x) ≤ ε—whose coordinates are integer multiples of 2−d, where d depends on K, ε, and the dimension m; in the absence of a Lipschitz constant K, there would be no such guarantee and the problem of computing fixed points would become intractable. Formally, the problem BROUWER is defined as follows.
BROUWER
Input: An efficient algorithm ΠF for the evaluation of a function F: [0, 1]m → [0, 1]m; a constant K such that F satisfies (4); and the desired accuracy ε.
Output: A point x such that d(F(x), x) ≥ ε.
It turns out that BROUWER is in PPAD. (Papadimitriou20 gives a similar result for a more restrictive class of BROUWER functions.) To prove this, we will need to construct an END OF THE LINE graph associated with a BROUWER instance. We do this by constructing a mesh of tiny triangles over the domain, where each triangle will be a vertex of the graph. Edges, between pairs of adjacent triangles, will be defined with respect to a coloring of the vertices of the mesh. Vertices get colored according to the direction in which F displaces them. We argue that if a triangle’s vertices get all possible colors, then F is trying to shift these points in conflicting directions, and we must be close to an approximate fixed point. We elaborate on this in the next few paragraphs, focusing on the two-dimensional case.
Triangulation: First, we subdivide the unit square into small squares of size determined by ε and K, and then divide each little square into two right triangles (see Figure 7, ignoring for now the colors, shading, and arrows). (In the m-dimensional case, we subdivide the m-dimensional cube into m-dimensional cubelets, and we subdivide each cubelet into the m-dimensional analog of a triangle, called an m-simplex.)
Coloring: We color each vertex x of the triangles by one of three colors depending on the direction in which F maps x. In two dimensions, this can be taken to be the angle between vector F(x) – x and the horizontal. Specifically, we color it red if the direction lies between 0 and −135°, blue if it ranges between 90 and 225°, and yellow otherwise, as shown in Figure 6. (If the direction is 0°, we allow either yellow or red; similarly for the other two borderline cases.) Using the above coloring convention the vertices get colored in such a way that the following property is satisfied:
(P1): None of the vertices on the lower side of the square uses red, no vertex on the left side uses blue, and no vertex on the other two sides uses yellow. Figure 7 shows a coloring of the vertices that could result from the function F; ignore the arrows and the shading of triangles.
Sperner’s Lemma: It now follows from an elegant result in Combinatorics called Sperner’s Lemma20 that, in any coloring satisfying Property (P1), there will be at least one small triangle whose vertices have all three colors (verify this in Figure 7; the trichromatic triangles are shaded). Because we have chosen the triangles to be small, any vertex of a trichromatic triangle will be an approximate fixed point. Intuitively, since F satisfies the Lipschitz condition given in (4), it cannot fluctuate too fast; hence, the only way that there can be three points close to each other in distance, which are mapped in three different directions, is if they are all approximately fixed.
The Connection with PPAD: …is the proof of Sperner’s Lemma. Think of all the triangles containing at least one red and yellow vertex as the nodes of a directed graph G. There is a directed edge from a triangle T to another triangle T’ if T and T‘ share a red-yellow edge which goes from red to yellow clockwise in T (see Figure 7). The graph G thus created consists of paths and cycles, since for every T there is at most one T‘ and vice versa (verify this in Figure 7). Now, we may also assume: On the left side of the square there is only one change from yellow to red.c Under this assumption, let T* be the unique triangle containing the edge where this change occurs (in Figure 7, T* is marked by a diamond). Observe that, if T* is not trichromatic (as is the case in Figure 7), then the path starting at T* is guaranteed to have a sink, since it cannot intersect itself, and it cannot escape outside the square (notice that there is no red-yellow edge on the boundary that can be crossed outward). But, the only way a triangle can be a sink of this path is if the triangle is trichromatic. This establishes that there is at least one trichromatic triangle. (There may of course be other trichromatic triangles, which would correspond to additional sources and sinks in G, as in Figure 7.) G is a graph of the kind in Figure 5. To finish the reduction from BROUWER to END OF THE LINE, notice that given a triangle it is easy to compute its colors by invoking ΠF, and find its neighbors in G (or its single neighbor, if it is trichromatic).
Finally, from Nash to Brouwer: To finish our proof that NASH is in PPAD we need a reduction from NASH to BROUWER. Such a reduction was essentially given by Nash himself in his 1950 proof: Suppose that the players in a game have chosen some (mixed) strategies. Unless these already constitute a Nash equilibrium, some of the players will be unsatisfied, and will wish to change to some other strategies. This suggests that one can construct a “preference function” from the set of players’ strategies to itself, that indicates the movement that will be made by any unsatisfied players. An example, of how such a function might look, is shown in Figure 8. A fixed point of such a function is a point that is mapped to itself—a Nash equilibrium. And Brouwer’s fixed point theorem, explained above, guarantees that such a fixed point exists. In fact, it can be shown that an approximate fixed point corresponds to an approximate Nash equilibrium. Therefore, NASH reduces to BROUWER.
4. From PPAD Back to NASH
To show that NASH is complete for PPAD, we show how to convert an END OF THE LINE graph into a corresponding game, so that from an approximate Nash equilibrium of the game we can efficiently construct a corresponding end of the line. We do this in two stages. The graph is converted into a Brouwer function whose domain is the unit three-dimensional cube. The Brouwer function is then represented as a game. The resulting game has too many players (their number depends on the size of the circuits that compute the edges of the END OF THE LINE graph), and so the final step of the proof is to encode this game in terms of another game, with three players.
4.1. From paths to fixed points: The PPAD-completeness of BROUWER
We have to show how to encode a graph G, as described in Figure 5, in terms of a continuous, easy-to-compute Brouwer function F—a very different-looking mathematical object. The encoding is unfortunately rather complicated, but is the key to the PPAD-completeness result…
We proceed by, first, using the three-dimensional unit cube as the domain of the function F. Next, the behavior of F shall be defined in terms of its behavior on a (very fine) rectilinear mesh of “grid points” in the cube. Thus, each grid point lies at the center of a tiny “cubelet,” and the behavior of F away from the centers of the cubelets shall be gotten by interpolation with the closest grid points.
Each grid point x shall receive one of four “colors” {0, 1, 2, 3}, that represent the value of the three-dimensional displacement vector F(x) – x. The four possible vectors can be chosen to point away from each other such that F(x) – x can only be approximately zero in the vicinity of all the four colors.
We are now ready to fit G itself into the above framework. Each of the 2n vertices of G shall correspond with two special sites in the cube, one of which lies along the bottom left-hand edge in Figure 9 and the other one along the top left edge. (We use locations that are easy to compute from the identity of a vertex of G.) While most other grid points in the cube get color 0 from F, at all the special sites a particular configuration of the other colors appears. If G has an edge from node u to node ν, then F shall also color a long sequence of points between the corresponding sites in the cube (as shown in Figure 9), so as to connect them with sequences of grid points that get colors 1, 2, and 3. The precise arrangement of these colors can be chosen to be easy to compute (using the circuits P and S that define G) and such that all four colors are adjacent to each other (an approximate fixed point) only at sites that correspond to an “end of the line” of G.
Having shown earlier that BROUWER is in PPAD, we establish the following:
THEOREM 4.1. BROUWER is PPAD-complete.
The PPAD-complete class of Brouwer functions that we identified above have the property that their function F can be efficiently computed using arithmetic circuits that are built up using a small repertoire of standard operators such as addition, multiplication, and comparison. These circuits can be written down as a “data flow graph,” with one of these operators at each node. In order to transform this into a game whose Nash equilibria correspond to (approximate) fixed points of the Brouwer function, we introduce players for every node on this data flow graph.
Games that Do Arithmetic: The idea is to simulate each arithmetic gate in the circuit by a game, and then compose the games to get the effect of composing the gates. The whole circuit is represented by a game with many players, each of whom “holds” a value that is computed by the circuit. We give each player two actions, “stop” and “go.” To simulate, say, multiplication of two values, we can choose payoffs for three players x, y, and z such that, in any Nash equilibrium, the probability that z (representing the output of the multiplication) will “go” is equal to the product of the probabilities that x and y will “go.” The resulting “multiplication gadget” (see Figure 10) has a fourth player w who mediates between x, y, and z. The directed edges show the direct dependencies among the players’ payoffs. Elsewhere in the game, z may input his value into other related gadgets.
Here is how we define payoffs to induce the players to implement multiplication. Let X, Y, Z, and W denote the mixed strategies (“go” probabilities) of x, y, z, and w. We pay w the amount $X · Y for choosing strategy stop and $Z for choosing go. We also pay z to play the opposite from player w. It is not hard to check that in any Nash equilibrium of the game thus defined, it must be the case that Z = X · Y. (For example, if Z > X · Y, then w would prefer strategy go, and therefore z would prefer stop, which would make Z = 0, and would violate the assumption Z > X · Y.) Hence, the rules of the game induce the players to implement multiplication in the choice of their mixed strategies.
By choosing different sets of payoffs, we could ensure that Z = X + Y or Z =½X. It is a little more challenging to simulate the comparison of two real values, which also is needed to simulate the Brouwer function. Below we discuss that issue in more detail.
Computing a Brouwer function with games: Suppose we have a Brouwer function F defined on the unit cube. Include three players x1, x2, and x3 whose “go” probabilities represent a point x in the cube. Use additional players to compute F(x) via gadgets as described above. Eventually, we can end up with three players y1, y2, and y3 whose “go” probabilities represent F(x). Finally, we can give payoffs to x1, x2, and x3 that ensure that in any Nash equilibrium, their probabilities agree with y1, y2, and y3. Then, in any Nash equilibrium, these probabilities must be a fixed point of F.
The Brittle Comparator Problem: There’s just one catch: our comparator gadget, whose purpose is to compare its inputs and output a binary signal according to the outcome of the comparison, is “brittle” in that if the inputs are equal then it outputs anything. This is inherent, because one can show that, if a nonbrittle comparator gadget existed, then we could construct a game that has no Nash equilibria, contradicting Nash’s theorem. With brittle comparators, our computation of F is faulty on inputs that cause the circuit to make a comparison of equal values. We solve this problem by computing the Brouwer function at a grid of many points near the point of interest, and averaging the results, which makes the computation “robust,” but introduces a small error in the computation of F. Therefore, the construction described above approximately works, and the three special players of the game have to play an approximate fixed point at equilibrium.
The Final Step: Three Players: The game thus constructed has many players (the number depends mainly on how complicated the program for computing the function F was), and two strategies for each player. This presents a problem: To represent such a game with n players we need n2n numbers—the utility of each player for each of the 2n strategy choices of the n players. But our game has a special structure (called a graphical game, see Kearns et al.15): The players are vertices of a graph (essentially the data flow graph of F), and the utility of each player depends only on the actions of its neighbors.
The final step in the reduction is to simulate this game by a three-player normal form game—this establishes that NASH is PPAD-complete even in the case of three players. This is accomplished as follows: We color the players (nodes of the graph) by three colors, say red, blue, and yellow, so that no two players who play together, or two players who are involved in a game with the same third player, have the same color (it takes some tweaking and argument to make sure the nodes can be so colored). The idea is now to have three “lawyers,” the red lawyer, the blue lawyer, and the yellow lawyer, each represent all nodes with their color, in a game involving only the lawyers. A lawyer representing m nodes has 2m actions, and his mixed strategy (a probability distribution over the 2m actions) can be used to encode the simpler stop/ go strategies of the m nodes. Since no two adjacent nodes are colored the same color, the lawyers can represent their nodes without a “conflict of interest,” and so a mixed Nash equilibrium of the lawyers’ game will correspond to a mixed Nash equilibrium of the original graphical game.
But there is a problem: We need each of the “lawyers” to allocate equal amounts of probability to their customers; however, with the construction so far, it may be best for a lawyer to allocate more probability mass to his more “lucrative” customers. We take care of this last difficulty by having the lawyers play, on the side and for high stakes, a generalization of the rock-paper-scissors game of Figure 1, one that forces them to balance the probability mass allocated to the nodes of the graph. This completes the reduction from graphical games to three-player games, and the proof.
5. Related Technical Contributions
Our paper 7 was preceded by a number of important papers that developed the ideas outlined here. Scarf’s algorithm21 was proposed as a general method for finding approximate fixed points, more efficiently than brute force. It essentially works by following the line in the associated END OF THE LINE graph described in Section 3.1. The Lemke-Howson algorithm17 computes a Nash equilibrium for two-player games by following a similar END OF THE LINE path. The similarity of these algorithms and the type of parity argument used in showing that they work inspired the definition of PPAD in Papadimitriou.20
Three decades ago, Bubelis1 considered reductions among games and showed how to transform any k-player game to a three-player game (for k > 3) in such a way that given any solution of the three-player game, a solution of the k-player game can be reconstructed with simple algebraic operations. While his main interest was in the algebraic properties of solutions, his reduction is computationally efficient. Our work implies this result, but our reduction is done via the use of graphical games, which are critical in establishing our PPAD-completeness result.
Only a few months after we announced our result, Chen and Deng2, 3 made the following clever, and surprising, observation. The graphical games resulting from our construction are not using the multiplication operation (except for multiplication by a constant), and therefore can even be simulated by a two-player game, leading to an improvement of our hardness result from three- to two-player games. This result was unexpected, one reason being that the probabilities that arise in a two-player Nash equilibrium are always rational numbers, which is not the case for games with three or more players.
Our results imply that finding an ε-Nash equilibrium is PPAD-complete, if ε is inversely proportional to an exponential function of the game size. Chen et al.3 extended this result to the case where ε is inversely proportional to a polynomial in the game size. This rules out a fully polynomial-time approximation scheme for computing approximate equilibria.
Finally, in this paper, we have focused on the complexity of computing an approximate Nash equilibrium. Etessami and Yannakakis9 develop a very interesting complexity theory of the problem of computing the exact equilibrium (or other fixed points), a problem that is important in applications outside Game Theory, such as Program Verification.
6. Conclusion and Future Work
Our hardness result for computing a Nash equilibrium raises concerns about the credibility of the mixed Nash equilibrium as a general-purpose framework for behavior prediction. In view of these concerns, the main question that emerges is whether there exists a polynomial-time approximation scheme (PTAS) for computing approximate Nash equilibria. That is, is there an algorithm for ε-Nash equilibria which runs in time polynomial in the game size, if we allow arbitrary dependence of its running time on 1/ε? Such an algorithm would go a long way towards alleviating the negative implications of our complexity result. While this question remains open, one may find hope (at least for games with a few players) in the existence of a subexponential algorithm18 running in time 0(nlogn/ε2), where n is the size of the game.
How about classes of concisely represented games with many players? For a class of “tree-like” graphical games, a PTAS has been given in Daskalakis and Papadimitriou,6 but the complexity of the problem is unknown for more general low-degree graphs. Finally, another positive recent development7 has been a PTAS for a broad and important class of games, called anonymous. These are games in which the players are oblivious to each other’s identities; that is, each player is affected not by who plays each strategy, but by how many play each strategy. Anonymous games arise in many settings, including network congestion, markets, and social interactions, and so it is reassuring that in these games approximate Nash equilibria can be computed efficiently.
An alternative form of computational hardness, exemplified in Hart and Mansour,14 arises where instead of identifying problems that are resistant to any efficient algorithm, one identifies problems that are resistant to specific “natural” algorithms. In Hart,14 lower bounds are shown for “decoupled” dynamics, a model of strategic interaction in which there is no central controller to find an equilibrium. Instead, the players need to obtain one in a decentralized manner. The study and comparison of these models will continue to be an interesting research theme.
Finally, an overarching research question for the Computer Science research community investigating game-theoretic issues, already raised in Friedman and Shenker10 but made a little more urgent by the present work, is to identify novel concepts of rationality and equilibrium, especially applicable in the context of the Internet and its computational platforms.
Figures
Figure 1. Rock-paper-scissors.
Figure 2. Three other two-player games.
Figure 3. Megiddo’s proof that NASH is unlikely to be NP-complete.
Figure 4. Writing down the problem algebraically.
Figure 5. END OF THE LINE: An apparently hard total search problem.
Figure 6. The colors assigned to the different directions of F(x) – x. There is a transition from red to yellow at 0°, from yellow to blue at 90°, and from blue to red at 225°.
Figure 7. The subdivision of the square into smaller squares, and the coloring of the vertices of the subdivision according to the direction of F(x) – x. The arrows correspond to the END OF THE LINE graph on the triangles of the subdivision; the source T * is marked by a diamond.
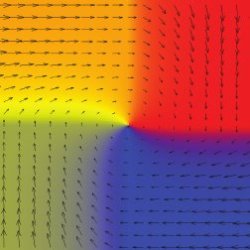
Figure 8. An illustration of Nash’s function FN for the penalty shot game. The horizontal axis corresponds to the probability by which the penalty kicker kicks right, and the vertical axis to the probability by which the goalkeeper dives left. The arrows show the direction and magnitude of FN(x) – x. The unique fixed point of FN is (1/2, 1/2) corresponding to the unique mixed Nash equilibrium of the penalty shot game. The colors respect
Figure 9. Embedding the END OF THE LINE graph in a cube. The embedding is used to define a continuous function F, whose approximate fixed points correspond to the unbalanced nodes of the END OF THE LINE graph.
Figure 10. The players of the multiplication game. The graph shows which players affect other players’ payoffs.
Join the Discussion (0)
Become a Member or Sign In to Post a Comment