Structural Characterizations of Schema-Mapping Languages

Information integration is a key challenge faced by all major organizations, business and governmental ones alike. Two research facets of this challenge that have received considerable attention in recent years are data exchange and data integration. The study of data exchange and data integration has been facilitated by the systematic use of schema mappings, which are high-level specifications that describe the relationship between two database schemas. Schema mappings are typically expressed in declarative languages based on logical formalisms and are chosen with two criteria in mind: (a) expressive power sufficient to specify interesting data interoperability tasks and (b) desirable structural properties, such as query rewritability and existence of universal solutions, that, in turn, imply good algorithmic behavior.

Here, we examine these and other fundamental structural properties of schema mappings from a new perspective by asking: How widely applicable are these properties? Which schema mappings possess these properties and which do not? We settle these questions by establishing structural characterizations to the effect that a schema mapping possesses certain structural properties if and only if it can be specified in a particular schema-mapping language. More concretely, we obtain structural characterizations of schema-mapping languages such as global-as-view (GAV) dependencies and local-as-view (LAV) dependencies. These results delineate the tools available in the study of schema mappings and pinpoint the properties of schema mappings that one stands to gain or lose by switching from one schema-mapping language to another.

Back to Top

1. Introduction

The aim of information integration is to synthesize information distributed over multiple heterogeneous sources into a single unified format. Information integration has been recognized as a key (and costly) challenge faced by large organizations today (see Bernstein and Haas^3,12). It is also well understood¹² that information integration is not a single problem but, rather, a collection of interrelated problems that include extracting and cleaning data from the sources, deriving a unified format for the integrated data, transforming data from the sources into data conforming with the unified format, and answering queries over the unified format. In this article, we focus on relational information integration, this is to say, we assume that the sources are databases over (different) relational schemas, called source or local schemas, and also that the unified format is some other relational schema, called the target or the global schema. A relational schema or simply a schema consists of names of relations and names of the columns of each relation. A database instance or simply an instance for a given schema is a collection containing, for each relation name in the schema, a finite relation (i.e., a table of records). An example of a source schema and a target schema is given in Figure 1. The source schema consists of three relation names that contain information about direct orders from a manufacturer together with information about retail sales; the target schema consists of a single relation name intended to summarize the sales records. Figure 1 also depicts a source instance and three target instances that will be used later on to illustrate the main concepts.

Two important facets of information integration are data exchange and data integration. Both these facets deal with the attainment of information integration, but they adopt distinctly different approaches. Data exchange is the problem of transforming data residing in different sources into data structured under a target schema; in particular, data exchange entails the materialization of data, after the data have been extracted from the sources and restructured into the unified format. In contrast, data integration can be described as symbolic or virtual integration: users are provided with the capability to pose queries and obtain answers via the unified format interface, while the data remain in the sources and no materialization of the restructured data takes place. Figure 2 depicts the data integration and data-exchange tasks.

In both data exchange and data integration, the relationship between the local schemas and the global schema must be spelled out. One way to accomplish this is via programs or SQL scripts written by human experts; this, however, can be an expensive and error-prone undertaking due to the complexity of the transformations involved. Instead, the research community has introduced schema mappings, a higher level of abstraction that makes it possible to separate the specification of the relationship between the schemas from the actual implementation of the transformations. Schema mappings are declarative specifications that describe the relationship between two database schemas. In recent years, schema mappings have been used extensively in specifying data interoperability tasks and are regarded as the essential building blocks in data exchange and data integration (see, e.g., the surveys^14,15). The use of schema mappings helps the user understand and reason about the relationship between the source schemas and the target schema; furthermore, schema mappings can be automatically compiled into executable scripts in various languages.

A concrete example of a schema mapping is given in Figure 1. The schema mapping is specified by two sentences of first-order logic. The first sentence asserts that whenever the source relation DirectCustomer contains a triple (v₁, v₂, v₃) of values and the source relation DirectOrder contains a quadruple (v₁, v₄, v₅, v₆) of values so that the values for cust-id in these two tuples coincide, then the target relation Sales must contain the quadruple (v₁, v₂, v₄, v₅). The second sentence asserts that whenever the source relation Retail contains a quadruple (w₁, w₂, w₃, w₄) of values, then there must exist some value V so that the target relation Sales contains the quadruple (w₂, V, w₃, w₄). Clearly, the pair (I, J₁) consisting of the source relation I and the target relation J₁ satisfies both these formulas; the same holds true for the pair (I, J₂). In contrast, the pair (I, J₃) fails to satisfy the first formula because the Sales relation does not contain the required quadruple (05-01-2009, UCSC, TFT-933SN-Wide, 100).

This example also unveils some of the main conceptual and algorithmic issues arising in data exchange and data integration. On the data exchange side, suppose that we wish to transform the above source instance I to a target instance J according to the schema mapping in Figure 1. There are at least two distinct target instances that, together the source instance I, satisfy the specification of the schema mapping; in fact, it is easy to see that there are infinitely many such target instances. So, which one should we choose to materialize? What makes one target instance a “better” candidate to materialize than another, and how can one be computed? As we shall see, universal solutions turn out to be the preferred target instances to materialize. On the data integration side, suppose that a user poses a query over the target schema. Different answers may be obtained by evaluating the query on different target instances that (together with the given source instance) satisfy the schema-mapping specification. So, what is the “right” semantics of target queries in data integration? Is it possible to rewrite target queries into queries over the source schema so that they can be evaluated directly against the given source instance? This will lead us to the notions of the certain answers and of allowing for query rewriting. In the next section, we will introduce some of the most commonly used schema-mapping languages, including global-as-view (GAV) dependencies and local-as-view (LAV) dependencies, and we will find out that schema mappings specified in these formalisms indeed admit universal solutions and allow for rewriting of the most frequently asked queries in relational databases (see Figure 2).

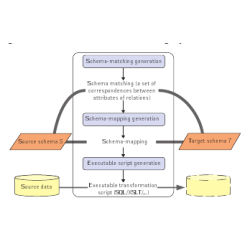
A system that makes systematic use of schema mappings is Clio, a data-exchange system that started as a research prototype at the IBM Almaden Research Center and is now part of IBM’s suite of information integration tools.¹³ The architecture of Clio is depicted in Figure 3. The system has a schema-matching component, a schema-mapping generation component, and an executable-script generation component. The schema-matching component produces a set of correspondences between attributes of relations in a source schema and a target schema; these correspondences are derived automatically or semi-automatically through an interaction with the user and via a graphical user interface that allows the user to intervene and make changes. The schema-mapping generation component takes as input these attribute correspondences and returns a schema mapping. In general, there are more than one schema mapping that are consistent with a set of attribute correspondences. Clio produces just one of these possible schema mappings but the user can again intervene and edit the schema mapping returned by the system. Finally, the executable-script generation component automatically transforms this schema mapping into a set of scripts in some language, such as SQL or XSLT.

Back to Top

2. Schema Mappings and Languages

In this section, we define the basic notions about schema mappings and present some of the main schema-mapping languages studied by the research community.

 2.1. Basic notions

A (relational) schema is a tuple R = (R₁, …, R_n) of relation symbols each of which has a fixed arity (number of attributes). An R–instance is a tuple I = (R₁^I, …, R_n^I) of finite relations, whose arities match those of the relation symbols of R. A fact of I is an expression R_i a, where i ≤ n and a is a tuple of values belonging to the relation R_i^I. The active domain of I, denoted by adom (I), is the set of all values occurring in the relation R_i^I, for 1 ≤ i ≤ n. We will be usually working with two disjoint schemas, called the source schema S = (S₁, …, S_n) and the target schema T = (T₁, …, T_m). An S-instance is called a source instance and a T-instance is called a target instance. Whenever we consider a pair of instances (I, J), it is understood that I is a source instance and J is a target instance.

As stated earlier, a schema mapping is a declarative specification that describes the relationship between two schemas. More precisely, a schema mapping is a triple M = (S, T, Σ), where S is a source schema, T is a target schema disjoint from S, and Σ is a set of sentences (i.e., formulas with no free variables) in some logical formalism. This is the syntactic view of schema mappings. There is also a complementary semantic view of schema mappings that we present next. Let I be a source instance and J a target instance. We say that J is a solution for I w.r.t. a schema mapping M = (S, T, Σ) if (I, J) = Σ, which means that (I, J) satisfies every sentence in Σ. Consequently, from a semantic standpoint, a schema mapping M can be thought of as a triple M = (S, T, Σ), where W is the set of all pairs (I, J) such that J is a solution for I w.r.t. M. So, as a semantic object, a schema mapping M is triple M = (S, T, W), where S is a source schema, T is a target schema disjoint from S, and W is a collection of pairs (I, J) with I a source instance and J a target instance.

Let L be a logical language, let Σ be a set of L-sentences, and let M = (S, T, W) be a schema mapping given as a semantic object. We say that M is L-definable by Σ if for every source instance I and every target instance J, we have that (I, J) W if and only if (I, J) Σ. When we work with schema mappings in the sequel, it will be clear from the context if the schema mapping at hand is viewed as a syntactic object or as a semantic one.

EXAMPLE 2.1. To illustrate these notions, consider the schema mapping in Figure 1. In this example, the source schema S consists of the relations DirectCustomer, DirectOrder, and Retail, while the target schema T consists of the single relation Sales. The relationship between source and target is then described by the schema mapping M = (S, T, Σ), where Σ consists of the two first-order sentences listed in Figure 1. As a semantic object, M is the triple (S, T, W), where W consists of all pairs (I, J) satisfies the two sentences in Σ. In particular, the pairs (I, J₁) and (I, J₂) belong to W, but the pair (I, J₃) does not. In other words, J₁ and J₂ are solutions for I w.r.t. to M, but J₃ is not.

 2.2. Schema-mapping languages

What is a “good” language for specifying schema mappings? To address this question, let us reflect on the relational database model, introduced by E.F. Codd 40 years ago.⁴ One of the reasons for the success of this model is that it supports powerful, high-level database query languages, such as relational algebra and relational calculus, that have formed the foundation for SQL. Relational algebra and relational calculus have the same expressive power as first-order logic⁵; in fact, relational calculus is a syntactic variant of first-order logic tailored for databases. Thus, at first sight, it is natural to ask: can first-order logic also be used as a schema-mapping language? It is not hard to show, however, that basic algorithmic problems in data integration and data exchange, such as existence-of- solutions and query answering, become undecidable if unrestricted use of first-order logic is allowed in specifying the relationship between database schemas (intuitively, this is so because such tasks involve testing first-order sentences for satisfiability, since they quantify over all solutions of a source instance). Consequently, we have to identify proper sublanguages of first-order logic that strike a good balance between expressive power for data interoperability purposes and algorithmic properties. Towards this goal, let us consider the following basic tasks that every schema-mapping language ought to support.

• Copy (nicknaming): Copy a source relation into a target relation and rename it.
• projection (Column Deletion): Form a target relation by deleting one or more columns of a source relation.
• Augmentation (Column Addition): Form a target relation by adding one or more columns to a source relation.
• Decomposition: Decompose a source relation into two or more target relations.
• Join: Form a target relation by joining two or more source relations.
• Combinations of the above: For example, combine join with column augmentation.

These tasks can be easily specified in first-order logic, as shown next. For concreteness, we use relations of arities two or three.

Observe that the above formulas have a striking syntactic similarity. As a matter of fact, they all belong to a class of first-order formulas called source-to-target tuple generating dependencies that we define in what follows.

• If R = (R₁, …, R_n) is a relational schema, then an atomic formula over R is an expression of the form R_i (x), where i ≤ n and x is a tuple of variables of length equal to the arity of R_i.
• A tuple-generating dependency (tgd) is a first-order formula of the form

• where x and y are tuples of variables, (x) is a conjunction of atomic formulas with variables in x, each variable in x occurs in at least one conjunct of (x), and Ψ(x, y) is a conjunction of atomic formulas with variables among those in x and y.

• A full tgd is a tgd with no existential quantifiers in the right-hand side, i.e., it is of the form x( (x) → Ψ(x)).

• A source-to-target tuple-generating dependency (s-t tgd) is a tgd such that (x) is a conjunction of atomic formulas over a source schema S and Ψ(x, y) is a conjunction of atomic formulas over a target schema T.

Informally, s-t tgds assert that if a pattern of facts appears in the source, then another pattern of facts must appear in the target. They are also known as global-and-local-as-view (GLAV) dependencies. In recent years, s-t tgds have been studied extensively in the context of data exchange and data integration^{14, 15} because, in spite of their syntactic simplicity, they can express many data interoperability tasks arising in applications. Furthermore, s-t tgds have desirable structural properties that we will discuss in the next section. The following two types of dependencies are important special cases of s-t tgds.

• A GAV dependency is an s-t tgd in which the right-hand side of the implication consists of a single atomic formula. Thus, a GAV dependency is of the form

• with (x) a conjunction of atomic formulas over a source schema and U(x‘) an atomic formula over a target schema such that the variables in x‘ are among those in x.

• A LAV dependency is an s-t tgd in which the left-hand side of the implication is a single atomic formula. Thus, a LAV dependency is of the form

• with R(x) an atomic formula over a source schema and Ψ(x, y) a conjunction of atomic formulas over a target schema.

Consider again the schema mapping in Figure 1. The first sentence used to specify that schema mapping is a GAV dependency, while the second one is a LAV dependency. Note also that the expressions for the Copy and the Projection tasks are both GAV and LAV dependencies, the expressions for the Augmentation and the Decomposition tasks are LAV dependencies, and the expression for the Join task is a GAV dependency. The expression for the Decomposition task is a full tgd. It is easy to see that every full tgd is logically equivalent to finitely many GAV dependencies. For example, the full tgd x, y, z(P(x, y, z) → U(x, y) V(y, z)) for the Decomposition task is logically equivalent to the set consisting of the GAV dependencies x, y, z(P(x, y, z) → U(x, y)) and x, y, z(P(x, y, z) → V(y, z)).

Before being used in data exchange and data integration, tuple-generating dependencies had been investigated in depth in the context of dependency theory during the 1970s and the 1980s. Dependency theory is the study of integrity constraints in databases; in this context, tuple-generating dependencies possess desirable algorithmic properties and contain as special cases many well-known classes of integrity constraints in databases, such as inclusion dependencies, join dependencies, and multi-valued dependencies.¹⁰ It is also interesting to note that tuple-generating dependencies seemed to have first appeared (at least in implicit form) a very long time ago. Indeed, in a recent article² presenting a formal system for Euclid’s Elements, the authors argue convincingly that the theorems in the Elements can be expressed using tuple-generating dependencies! Intuitively, this is so because the typical theorem of Euclidean Geometry states that if a certain pattern between geometric objects (points, lines, triangles, or circles) exists, then another pattern between geometric objects must also exist.

Back to Top

3. Properties of Schema Mappings

In this section, we present several structural properties of schema mappings, which have been widely used in the literature on data exchange and data integration. They will turn out to play a key role in our characterizations of schema-mapping languages. Before presenting these properties, however, we need to introduce some important notions in data exchange and data integration.

Homomorphisms. A central notion in the study of schema mappings is that of a homomorphism. Let K and K‘ be two instances over the same schema R = (R₁, …, R_n). A homomorphism for K to K‘ is a function from the active domain of K to the active domain of K‘ such that if (a₁, …, a_m) R_i^k, then (h(a₁, …, a_m)) R_i^k‘, for i = 1, …, n.

A homomorphism h is said to be constant on a set X if h restricted to X ∩ dom (h) is the identity function, i.e., h(x) = x, if x X and h(x) is defined. Here, we will consider homomorphisms between target instances and we will require that they are constant on the active domain of some source instance. The rationale behind this requirement is as follows. Typically, when data is exchanged from source to target, the elements in the active domain of a given source instance are “known” values. The schema mapping at hand, however, may under-specify the relationship between source and target. In turn, this may force using “unknown” values, called labeled nulls, to materialize solutions for a given source instance. Thus, target instances may have both “known” values, originating from the source instance, and “unknown” values, chosen freshly and acting as placeholders. An example of labeled null is the value N₁ in the target instance J₁ in Figure 1. Homomorphisms are required to leave “known” values untouched, but are free to replace an “unknown” value by another, “known” or “unknown”, value.

Universal Solutions. Let M = (S, T, Σ) be a schema mapping. Recall that if I is a source instance, then a solution for I w.r.t. M is a target instance J such that (I, J) = Σ. In general, a source instance I may have multiple solutions and, in fact, infinitely many; in particular, this holds true for schema mappings M specified by s-t tgds because if J is a solution for I w.r.t. M, then every instance J‘ containing J (as a set of facts) is also a solution for I. Which among those solutions should one materialize if I is to be transformed into a target instance? To address this question, the following concept of a universal solution was introduced in Fagin et al.⁷

Let M = (S, T, W) be a schema mapping and let I be a source instance. A target instance J is a universal solution for I if

1. J is a solution for I.
2. For each target instance J‘ that is a solution for I, there is a homomorphism h: J → J‘ that is constant on adom (I).

The intuition behind this concept, which is illustrated in Figure 4, is that a universal solutions is a “most general” solution in the sense that it contains no more and no less information than that specified by the given schema mapping.

EXAMPLE 3.1. Consider the source instance I in Figure 1. One solution for I with respect to the given schema mapping is the target instance J₁. Note that N₁ is a value that does not occur in I, and therefore is interpreted as a labeled null. Another solution for I is the target instance J₂, which is the same as J₁ except that labeled null value N₁ has been replaced by UCLA. However, J₂ contains information that is not implied by the schema mapping, namely, that the customer of the order on May 3, 2009 is UCLA, and, consequently, it is not a universal solution. Indeed, there is a homomorphism from J₁ to J₂ constant on the active domain of I (N₁ is mapped to UCLA), but not vice versa.

Queries and Certain Answers. Informally, a query is a question that a user poses against a database. More formally, a query q takes as input an instance K and returns as output a relation q(K) of fixed arity with values from the active domain of K. Suppose now that we have a schema mapping between a source schema and target schema. Suppose also that a query q over the target schema is posed and that a source instance I is given. What does answering q using the source instance I mean? As seen earlier, there may be infinitely many solutions J for a given source instance I; furthermore, if q is evaluated on different solutions J for I, it is possible that different answers are obtained each time. This ambiguity raises the conceptual problem of giving precise semantics to query answering in data exchange and data integration. The approach taken by the research community is to adopt the certain answers semantics, a semantics that originated in the study of incomplete databases (see van der Meyden¹⁹).

Let M = (S, T, Σ) be a schema mapping and q a query over the target schema T. If I is source instance, then the certain answers of q on I with respect to M, denoted certain _M(q)(I), is the set

The certain answers semantics provides the guarantee that if a tuple t belongs to certain _M(q)(I), then t belongs to the result q(J) of q on every solution J for I. It is easy to see that every tuple in certain _M(q)(I) is a tuple of values from I. Thus, every schema mapping M induces a (semantic) transformation certain_M from queries over the target schema to queries over the source schema, so that if q is query over the target schema, then this transformation associates to it the query certain_M (q) over the source schema that has the same arity as q and is defined by certain _M(q)(I) = ∩ {q(J): J is a solution for I w.r.t. M}.

On the face of it, the certain answers semantics is noneffective, since evaluating certain _M(q)(I) may entail computing the intersection of infinitely many sets. For many frequently asked queries, however, efficient algorithms for evaluating their certain answers exist.

A conjunctive query is a first-order formula of the form wX(x, w), where ξ(x, w) is a conjunction of atoms and/or equalities. Conjunctive queries are the most frequently asked queries in relational databases. They are also known as project select-join (SPJ) queries because they are precisely the queries that are expressible in relational algebra using the selection, projection, and join operations; in particular, conjunctive queries are easily expressible in SQL using the SELECT FROM WHERE construct. A union of conjunctive queries is a finite disjunction of conjunctive queries; equivalently, they are the queries expressible in relational algebra using the selection, projection, join, and union operations.

In information integration, the main approach to computing the certain answers is to try to rewrite queries over the target to queries over the source. In data exchange, one would like to take advantage of the materialized solution and use it to obtain the certain answers of target queries. Both approaches give rise to polynomial-time algorithms for computing the certain answers of unions of conjunctive queries. In particular, as shown in Fagin et al.,⁷ the certain answers of unions of conjunctive queries can be obtained using universal solutions. Specifically, let M = (S, T, Σ) be a schema mapping such that Σ is a finite set of s-t tgds and let q be a union of conjunctive queries over T. If I is a source instance and J is a universal solution for I, then certain_M (q)(I) = q(J)_↓, where q(J)_↓ is the result obtained by first computing q(J) and then keeping only those tuples that contain values from the active domain of I only.

EXAMPLE 3.2. Returning to the example schema mapping M and source instance I from Figure 1, consider the conjunctive query q over the target schema given by

It asks for all pairs of products (x, y), such that some customer bought x and y (in some quantities) on the same date. It is not hard to see that, for every solution J of I with respect to M, the pair (Quadcore-9950-PC,TFT-933SN-Wide) belongs to q(J). In other words, this tuple belongs to the certain answers of q in I with respect to M. It turns out that the certain answers of q on a source instance I are precisely the answers to q'(I), where q’ is the following union of conjunctive queries over the source schema:

Note that the Retail relation does not provide information about the name of the buyer, and therefore, can only contribute identity pairs to the certain answers of q.

Alternatively, the certain answers of q on I can be computed by evaluating q on the universal solution J₁ of I that we discussed in Example 3.1, and keeping only those tuples that contain only values from the active domain of I.

Structural Properties of Schema Mappings. Recall that a schema mapping M can be viewed as a syntactic object or as a semantic one. As a syntactic object, M is given by a triple (S, T, Σ), where Σ is a set of sentences in some logical formalism; as a semantic object, M is given by a triple (S, T, W), where W is a set of pairs (I, J) with I a source instance and J a target instance. In what follows, whenever we write that (I, J) M, we mean that (I, J) Σ or that (I, J) W depending on whether M is given as a syntactic object or a semantic one.

We are now ready to present the structural properties of schema mappings that will play a key role in our characterization results. We begin with three such properties that have been widely used in both data exchange and data integration.

DEFINITION 3.3. Let M be a schema mapping.

• Closure under target homomorphisms: We say that M is closed under target homomorphisms if for all (I, J) M and for all homomorphisms h: J → J’ that are constant on adom(I), we have that (I, J’)) M. (see Figure 5a).
• Admitting universal solutions: We say that M admits universal solutions if for each source instance I there is a universal solution J for I w.r.t. M.
• Allowing for conjunctive query rewriting: We say that M allows for conjunctive query rewriting if for each union q of conjunctive queries over the target schema, the certain answers query certain M(q) is definable by a union of conjunctive queries over the source schema. In other words, there is a union q’ of conjunctive queries over the source schema such that certain _M(q)(I) = q’(I), for every source instance I.

The first two conditions of closure under target homomorphisms and admitting universal solutions go very well together. As was observed in Fagin et al.,⁷ if a schema mapping is closed under target homomorphisms and admits universal solutions, then, for every source instance I, the (typically infinite) space of all solutions of I w.r.t. M can be completely described by just a single target instance J, namely, by any universal solution J for I. This is so because if J is universal for I and M is closed under target homomorphisms, then for every target instance J’, we have that J’ is a solution for I if and only if there is a homomorphism h:J → J’ that is constant on adom(I). We mention in passing that these two conditions together also imply the existence of core universal solutions, which are the smallest universal solutions (see Fagin et al.⁸). Thus, these two conditions lie at the foundation of data exchange. The third condition of allowing for conjunctive query rewriting is important in the context of data integration, since it implies that the certain answers of unions of conjunctive queries over the target are computable in polynomial time (in the sense of data complexity).

It is well known that all three conditions of closure under target homomorphisms, admitting universal solutions, and allowing for conjunctive query rewriting are possessed by every schema mapping M definable by a finite set of s-t tgds. Closure under homomorphisms follows easily from the definitions; admitting universal solutions was shown in Fagin et al.⁷ using the chase procedure. In the case of GAV dependencies, a union of conjunctive queries over the target is easily transformed to a union of conjunctive queries over the source by simply replacing each target relation symbol P by a union of conjunctive queries over the source that defines P. In the case of arbitrary s-t tgds, allowing for conjunctive query rewriting is proved by first “decomposing” the given s-t tgds into GAV dependencies and to LAV dependencies, and then applying results from Abiteboul and Duschka¹ and Duschka and Genesereth.⁶ We collect these results into one theorem.

THEOREM 3.4. Every schema mapping definable by a finite set of s-t tgds is closed under target homomorphisms, admits universal solutions, and allows for conjunctive query rewriting.

Next, we define three additional properties of schema mappings.

DEFINITION 3.5. Let M be a schema mapping.

• Closure Under target intersection: We say that M is closed under target intersection if for all source instances I and all target instances J₁, J₂ if (I, J₁) M and (I, J₂) M, then also (I, J₁ ∩ J₂) M. (See Figure 5b.)
• Closure Under Union: We say that M is closed under union if ( , ) M, and for all (I₁, J₁) M, and (I₂, J₂) M, we have that also (I₁ I₂, J₁ J₂) M. (See Figure 5c.)
• n-Modularity: Let n be a positive integer. We say that M is n-modular if whenever a pair (I, J) does not belong to M, there is a sub-instance I’ Í I such that |adom (I’)| ≤ n and (I’, J) does not belong to M.

Intuitively, a schema mapping is closed under union if solutions can be constructed in a “modular” fashion, i.e., on a tuple-by-tuple basis. Similarly, n-modularity asserts that if (I, J) M, then there is a concise explanation for this fact; this property can also be viewed as a relaxation of closure under union.

We now give several useful propositions about the properties we just introduced.

PROPOSITION 3.6. Let M be a schema mapping.

• If M is definable by a finite set of GAV dependencies, then M is closed under target intersection.
• If M is definable by a finite set of LAV dependencies, then M is closed under union.
• If M is definable by a finite set of s-t tgds, then M is n-modular for some n ≥1.

PROOF. The first two parts follow easily from the definitions. For the third part, assume that M is a schema mapping definable by a finite set Σ of s-t tgds. Let n be the maximum number of variables occurring in the left-hand side of the s-t tgds in Σ. We claim that M is n-modular. Assume that (I, J) ∉ M. Then there is some s-t tgd x( (x) → yΨ(x, y)) from Σ and a tuple a of values from adom(I) such that (I, J) (a) ¬ yΨ(a, y). Now, let I‘ be the sub-instance of I containing only the values a. Then, it is still the case that (I’, J) = (a) ¬ yΨ(a, y), and hence (I‘, J) ∉ M.

Back to Top

4. Language Characterizations

This section contains the main technical results of the paper, which yield structural characterizations of the various schema-mapping languages considered in earlier sections. We begin with schema mappings specified by LAV dependencies.

THEOREM 4.1. For all schema mappings M, the following are equivalent:

1. M is definable by a finite set of LAV dependencies.
2. M is closed under target homomorphisms, admits universal solutions, allows for conjunctive query rewriting, and is closed under union.

PROOF. The implication (1) (2) follows from Theorem 3.4 and Proposition 3.6. We now prove the implication (2) (1). The idea behind the proof is that, since M is closed under union, universal solutions for source instances I can be constructed out of universal solutions for parts of I. This implies that, in defining our schema mapping, we only need to take into account of finite number of source instances up to isomorphism, namely, those that contain precisely one tuple. In what follows, we will make this idea precise.

Suppose that M satisfies the listed conditions. Let R₁, …, R_n be the relations of the source schema, and let D be a set consisting of k distinct values, with k = max_i≤n arity(R_i). Let facts be the set of all possible facts, of the form R_i (d₁, …, d_l) with i ≤ n, l = arity(R_i), and d₁, …, d_l D. For each α facts, let I_α be a the source instance containing only the fact α, and let J_α be a universal solution for I_α. Let PosDiag_Iα (x) be the positive diagram of I_α, i.e., the conjunction of all facts true in I (which consists of precisely one fact) and let PosDiag_Jα (x, y) be the positive diagram of J_α where x are as many variables as there are elements of adom(I_α) and y as many variables as there are elements of adom(J_α) \ adom(I_α). Let _α be the following LAV dependency: x(PosDiag_Iα (x) → yPosDiag_Jα (x, y)). Finally, let 2 = { _α\α facts}. We claim that Σ defines M.

First, we prove soundness: every (I, J) M satisfies Σ. Suppose (I, J) M, and take any _α Σ. Furthermore, suppose that the antecedent of _α is satisfied in (I, J) under some variable assignment h. In other words, h is a homomorphism from I_α to I. Let q be the certain answer query of the conjunctive query yPosDiag_Jα (x, y). Since M allows for conjunctive query rewriting, q is definable by a union of conjunctive queries. Moreover, since yPosDiag_jα (x, y) is satisfied in J_α, which is a universal solution of I_α, it is satisfied in all solutions of I_α. In other words, q is satisfied in I_α, and hence, in I under the assignment h. Hence, (I, J) satisfies _α.

Next, we prove completeness: every pair (I, J) satisfying Σ belongs to M. Suppose (I, J) satisfies Σ. Write I as I = I₁ … I_n where each I_i contains only a single fact. Then each (I_i, J) still satisfies Σ. Since I_i contains a single fact, it must be isomorphic to I_α for some α facts. Using the fact that (I_i, J) satisfies _α, we can show that there is a homomorphism from a universal solution of I_i to J, constant on adom(I_i), hence, by closure under target homomorphisms, (I_i, J) M. It follows by closure under union that (I, J) M.

Our next result characterizes schema mappings specified by GAV dependencies.

THEOREM 4.2. For all schema mappings M, the following are equivalent:

1. M is definable by a finite set of GAV dependencies.
2. M is closed under target homomorphisms, admits universal solutions, allows for conjunctive query rewriting, and is closed under target intersection.

PROOF. (Hint) The implication (1) (2) follows from Theorem 3.4 and Proposition 3.6. For the implication (2) (1), we first show that every schema mapping M satisfying (2) is n-modular for some n > 0. For each target relation R, let q_R = certain_M (Ry), where y is a sequence of distinct fresh variables of appropriate length. Note that, since M allows for conjunctive query rewriting, q_R can be written as a union of conjunctive queries. Now, let n be the maximum of the number of variables occurring in each q_R. Using the hypothesis that M admits universal solutions, is closed under target homomorphisms, and is closed under target intersection, it can be shown that M is n-modular.

After this, the implication (2) (1) is established along the same lines as the proof of Theorem 4.1. Instead of considering all source instances consisting of one tuple, we consider all source instances I with |adom(I)| ≤ n. There are only finitely many such source instances up to isomorphism. Moreover, it can be shown, using closure under intersection, that each has a null-free universal solution, and hence only full s-t tgds are needed to describe them.

We now focus on schema mappings specified by arbitrary s-t tgds. As seen in Theorem 3.4, every schema mapping defined by a finite set of s-t tgds is closed under target homomorphisms, admits universal solutions, and allows for conjunctive query rewriting. The next result asserts that any schema mapping satisfying these conditions is definable by an infinite set of s-t tgds.

PROPOSITION 4.3. If a schema mapping M is closed under target homomorphisms, admits universal solutions, and allows for conjunctive query rewriting, then M is definable by an infinite set of s-t tgds.

PROOF. (Hint) Assume that M satisfies the listed properties. Consider a source instance I and a target instance J such that J is a universal solution for I with respect to M. For each element of adom(I), introduce a distinct variable x_i, and for each element of adom(J) \ adom(I), introduce a distinct variable y_j. Define PosDiag_I(x) to be the conjunction of all atomic formulas in x true in I (under the chosen assignment) and define PosDiag_I(x, y) like-wise. Finally, let Σ be the set of all s-t tgds _I,j of the form x(PosDiag_I(x) → y PosDiag_J(x,y)), where I is a source instance and J is a universal solution for I w.r.t. M. Using an argument analogous to the one used in the proof of Theorem 4.1, it can be shown that Σ defines M.

Can Proposition 4.3 be strengthened to a characterization of schema mappings specified by a finite set of s-t tgds? The next result, which was proved in Fagin et al.,⁹ shows that this is not possible.

PROPOSITION 4.4. The schema mapping defined by the first-order sentence x y z(Rxz → Syz) is closed under target homomorphisms, admits universal solutions, and allows for conjunctive query rewriting, but is not definable by any finite set of s-t tgds.

Can Proposition 4.3 be turned to a characterization of schema mappings specified by an infinite set of s-t tgds? The next observation shows that this is not possible.

PROPOSITION 4.5. The schema mapping defined by the following infinite set of s-t tgds does not admit universal solutions:

PROOF. (Hint) It is easy to see that no solution for I = {Pa} can be universal. Here, the assumption that all instances (hence all solutions) are finite is of the essence.

PROPOSITION 4.4 implies that additional properties must be considered in order to characterize the schema mappings that are definable by a finite set of s-t tgds. It turns out that the addition of n-modularity, for some n > 0, yields such a characterization.

THEOREM 4.6. For all schema mappings M, the following are equivalent:

1. M is definable by a finite set of s-t tgds.
2. M is closed under target homomorphisms, admits universal solutions, allows for conjunctive query rewriting, and is n-modular for some n > 0.

We conclude this section by commenting briefly on additional characterizations presented in the previous version of this paper.¹⁷ Observe that the condition of allowing for conjunctive query rewriting differs in nature from the other structural conditions: while the latter are model-theoretic conditions, the former refers to a certain syntactically defined class of queries. Thus, it is natural to ask: can the condition of allowing for conjunctive query rewriting be replaced by a condition of model-theoretic character? To this effect, we consider the notion of reflecting source homomorphisms, which states, roughly, that every homomorphism between source instances I, I’ extends to a homomorphism from any universal solution of I to any universal solution of I‘. We show that the structural characterizations of LAV dependencies in Theorem 4.1 and of s-t tgds in Theorem 4.6 hold with the condition of allowing for conjunctive query rewriting replaced by that of reflecting source homomorphisms. Further, we pursue characterizations where one assumes that the schema mapping is first-order definable to start with. We establish that, for all schema mappings M definable by a first order sentence, M is definable by a finite set of GAV dependencies if and only if M is closed under target homomorphisms, admits universal solutions, reflects source homomorphisms, and is closed under target intersection. The proof makes essential use of the sophisticated machinery developed by Rossman¹⁶ for proving the preservation-under-homomorphisms theorem in the finite.

Back to Top

5. Complexity of Definability

Our characterizations provide tools for testing whether a schema mapping defined in one language can also be defined in another language. For example, our results imply that a schema mapping defined by a finite set of s-t tgds is definable by a finite set of GAV dependencies if and only if it is closed under target intersection: furthermore, it is definable by a finite set of LAV dependencies if and only if it is closed under union. Here, we pinpoint the computational complexity of testing definability in the different languages.

First, assume that the input to the problem is a finite set of s-t tgds. The results are summarized in the following table.

The proofs also yield effective methods for constructing an equivalent schema mapping in the smaller language whenever it exists. Our proofs are based on reductions from definability problems to the entailment problem for s-t tgds; given two schema mappings M₁, M₂, specified by a finite set of s-t tgds, is it the case that whenever (I, J) M₁ also (I, J) M₂? We show that the latter problem in NP-complete; moreover, it is in PTIME if M₁ is specified by LAV dependencies and M₂ by GAV dependencies.

It is also natural to consider the problem of testing whether a schema mapping specified by a first-order sentence is definable in one of the schema-mapping languages studied here. This problem, however, turns out to be undecidable no matter what schema-mapping language we consider (s-t tgds, GAV dependencies, or LAV dependencies). This can be easily proved using the undecidability of satisfiability for first-order sentences in the finite.¹⁸

Back to Top

6. Discussion and Open Problems

The work presented here has methodological implications for the study of schema mappings. Concretely, our structural characterizations delineate the exact set of tools available in the study of schema mappings specified in particular languages. For example, consider the language of LAV dependencies. A perusal of the literature reveals that earlier results about schema mappings specified by a finite set of LAV dependencies made systematic use of the fact that such schema mappings are closed under target homomorphisms, admit universal solutions, allow for conjunctive query rewriting, and are closed under union. The structural characterization given in Theorem 4.1, in effect, turns the tables around and asserts that these four properties are the only properties one needs to use in reasoning about schema mappings specified by LAV dependencies. On the computational side, the complexity-theoretic results in Section 5 quantify in precise terms the difficulty of determining whether a schema mapping specified in one language can also be specified in a different language.

There has also been an extensive study of schema mappings specified using languages richer than the language of s-t tgds. Consider, for instance, schema mappings specified by s-t tgds and target tgds, which were studied in Fagin et al.,⁷ or schema mappings specified by second-order tgds (SO tgds), which arise when composing schema mappings specified by s-t tgds.⁹ These languages are known to be strictly more expressive than the language of s-t tgds. Our results then predict that these languages lack at least one of the structural properties considered here. Indeed, schema mappings specified by s-t tgds and target tgds are closed under target homomorphisms and admit universal solutions, but need not allow for conjunctive query rewriting. Likewise, schema mappings specified by SO tgds admit universal solutions and allow for conjunctive query rewriting, but need not be closed under target homomorphisms. It remains an open problem to establish structural characterizations for such richer languages of dependencies. A particularly interesting question is whether there is a natural way to characterize weakly acyclic sets of target tgds,⁷ a class of target dependencies that is of central importance in data exchange, as they guarantee termination of the chase procedure within a polynomial number of steps.

Among the properties of schema mappings considered here, closure under target homomorphisms, admitting universal solutions, and allowing for conjunctive query rewriting are arguably the most fundamental ones for data exchange and data integration. Proposition 4.4 tells that there are schema mappings satisfying these properties that cannot be defined by any finite set of s-t tgds. Is there a natural extension of the language of s-t tgds that is characterized by these three properties? In order to express transformations involving grouping and data merging, a proper extension of the language of s-t tgds, called nested s-t tgds, was proposed in Fuxman et al.¹¹ In the previous version of this paper,¹⁷ we showed that schema mappings specified by a finite set of nested s-t tgds are closed under target homomorphisms, admit universal solutions, allow for conjunctive query rewriting (but may not be n-modular for any n > 0). It is an open problem to determine whether all schema mappings satisfying these properties can be defined by nested s-t tgds.

Back to Top

Acknowledgments

Research on this paper was partially supported by NSF grants IIS-0430994 and ARRA 0905276, the Netherlands Organization for Scientific Research (NWO) grant 639.021.508, and the ERC Advanced Grant Webdam on Foundations of Web data management. Part of the work was carried out during a visit by Balder ten Cate at UC Santa Cruz and the IBM Almaden Research Center.

Back to Top

Back to Top

Back to Top

Back to Top

Back to top