Shields for Safe Reinforcement Learning

Integrating shields with reinforcement learning.  Shields are mechanisms that provide formal safety guarantees by preventing unsafe actions from being executed at runtime. Such a procedure is often referred to as runtime enforcement. Integrated into an RL setting, a shield prevents unsafe behavior of the learning agent during both the learning and deployment phases, while restricting the agent as little as possible.

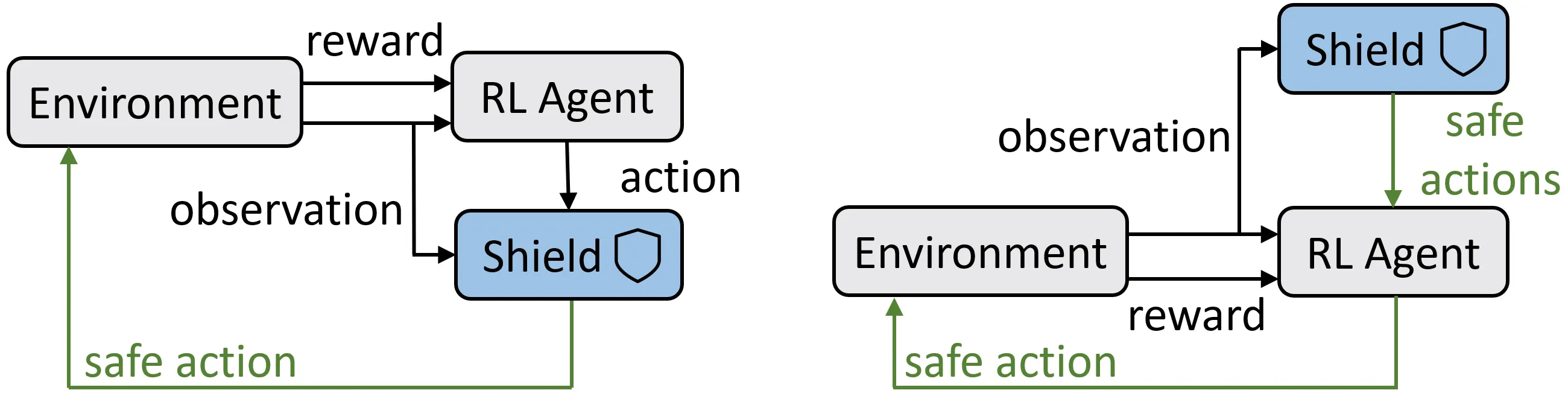
The main approaches to integrating a shield into RL are pre-shielding and post-shielding, which differ in how they intervene. Figure 3 (left) shows post-shielding: The shield is positioned between the agent and the environment, continuously monitoring the state of the environment and the actions selected by the agent. It evaluates the risk associated with the selected action, classifies the action as safe or unsafe, and replaces any unsafe action with a safe one. Figure 3 (right) illustrates pre-shielding, in which the shield provides a list of all safe actions, allowing the agent to select the best available option. Note that it is formally not possible to compute a shield if no safe action exists. In such cases, the practical solution is to lower the safety requirements, if possible.

Both options have their advantages and disadvantages. Several RL algorithms such as proximal policy optimization³⁷ and deep Q-learning²⁹ have masked versions⁴⁰ that take a list of forbidden actions as extra input, making pre-shielding simple to integrate. In this case, the final decision on which safe action to take remains with the learning algorithm. However, if no masked version of a learning algorithm exists, pre-shielding can be challenging to integrate.

The advantage of a post-shield is that it is generally easy to integrate, as it simply overwrites unsafe actions. However, a naive integration can negatively impact learning performance, for two reasons. First, by overwriting the agent’s actions, the shield may slow down the exploration of the environment. To mitigate this, the post-shielding algorithm can often select a “good” alternative for the agent, such as choosing an action similar to the one originally selected. Additionally, some learning algorithms provide a ranked list of actions, allowing the shield to choose the second-best option. Second, a post-shield can disrupt the association between an action and its reward. To address this, the reward should be tied to the action chosen by the shield rather than the agent’s original choice.

Shield computation and safety guarantees.  The essential property of a shield is its ability to provide provable safety guarantees during learning and deployment. To that end, shields are rigorously computed from a formal specification of safety-critical properties and an abstract model of the environment. This specification distinguishes permitted (safe) and forbidden (unsafe) behaviors and is independent of the agent’s learning objective. Thus, a shield maintains a clear separation between an agent’s safety and performance. Many formal approaches exist to derive shields, leveraging techniques from reactive synthesis,⁵ supervisory control,³⁵ theorem proving,¹⁵ or model checking.^3,11

The guarantees that a shield provides may be absolute or probabilistic (see later sections). When using deterministic models, the resulting shields treat safety as a qualitative, absolute measure. By taking only actions classified as safe, the specified safety-critical properties are guaranteed to never be violated, regardless of what may occur in the environment in the future. If this condition is not met, an action is deemed unsafe.

In real-world scenarios, absolute safety guarantees may be unrealistic. For example, an unmanned aerial vehicle (UAV) may not be able to rule out the possibility of colliding with other aerial vehicles when they behave highly irregularly. Thus, a low risk of a collision may be acceptable. For these situations, probabilistic models are used to compute shields that consider safety as a quantitative measure. An action is deemed unsafe if it induces an unacceptably high risk of compromising safety. To classify an action as safe or unsafe, a shield computes the probability of an action violating safety. Actions are classified as safe if this probability is below some threshold. By adjusting this threshold, shields can be generated that are either more liberal or more restrictive toward the agent.

Promise and limitations of shielding as an approach to combine symbolic and sub-symbolic AI.  Shielded RL combines model-based methods with DRL, providing provable safety guarantees and high performance. Shielding thus combines the benefits of sub-symbolic and symbolic AI. Neural networks can process large amounts of data to learn excellent approximations of ill-understood functions inductively and offer performance that cannot be matched by other methods. On the other hand, symbolic AI offers deductive, data-independent approaches that are less performant but provide guarantees. However, shielding suffers inherently from the limitations of model-based verification. To provide safety guarantees, one has to employ techniques such as model checking. Though state-of-the-art shielding approaches are able to handle environments with billions of states,¹⁹ real-world applications may demand far larger scalability.

Core questions of shielded reinforcement learning.  We will discuss the following core questions of shielded RL:

• What types of safety guarantees can be provided by a shield, and under which assumptions?

• How can shields be computed?

• How can shields be integrated in RL?

• What are the challenges in shielded RL?

The purpose of this article is to discuss these questions and to shed light on the current state of the art of shielded learning.

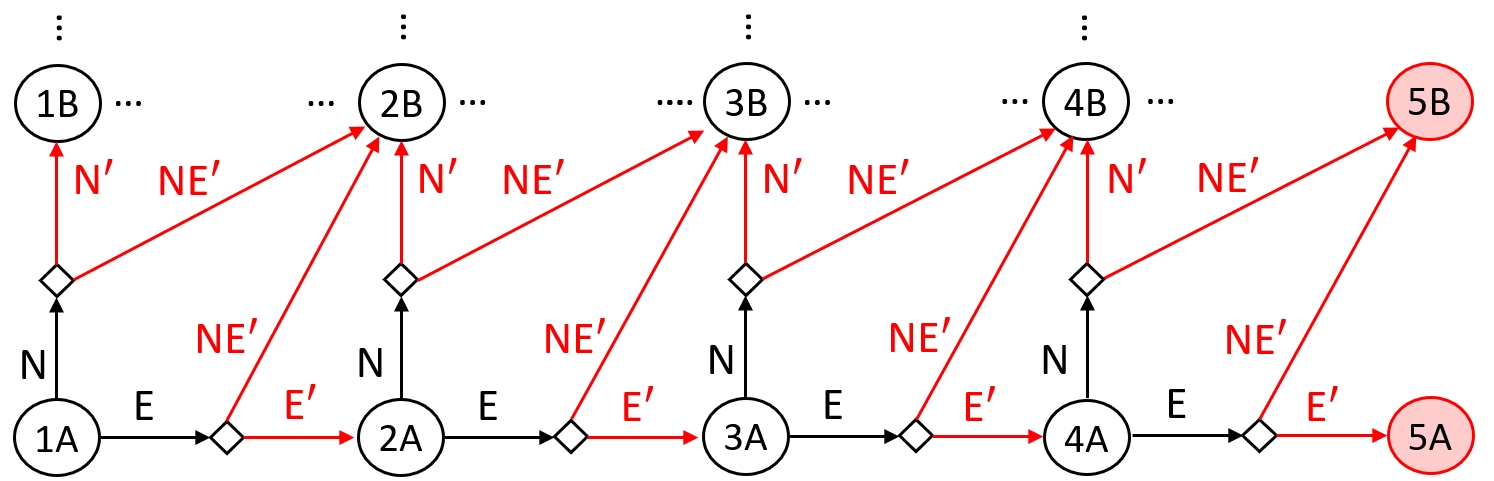
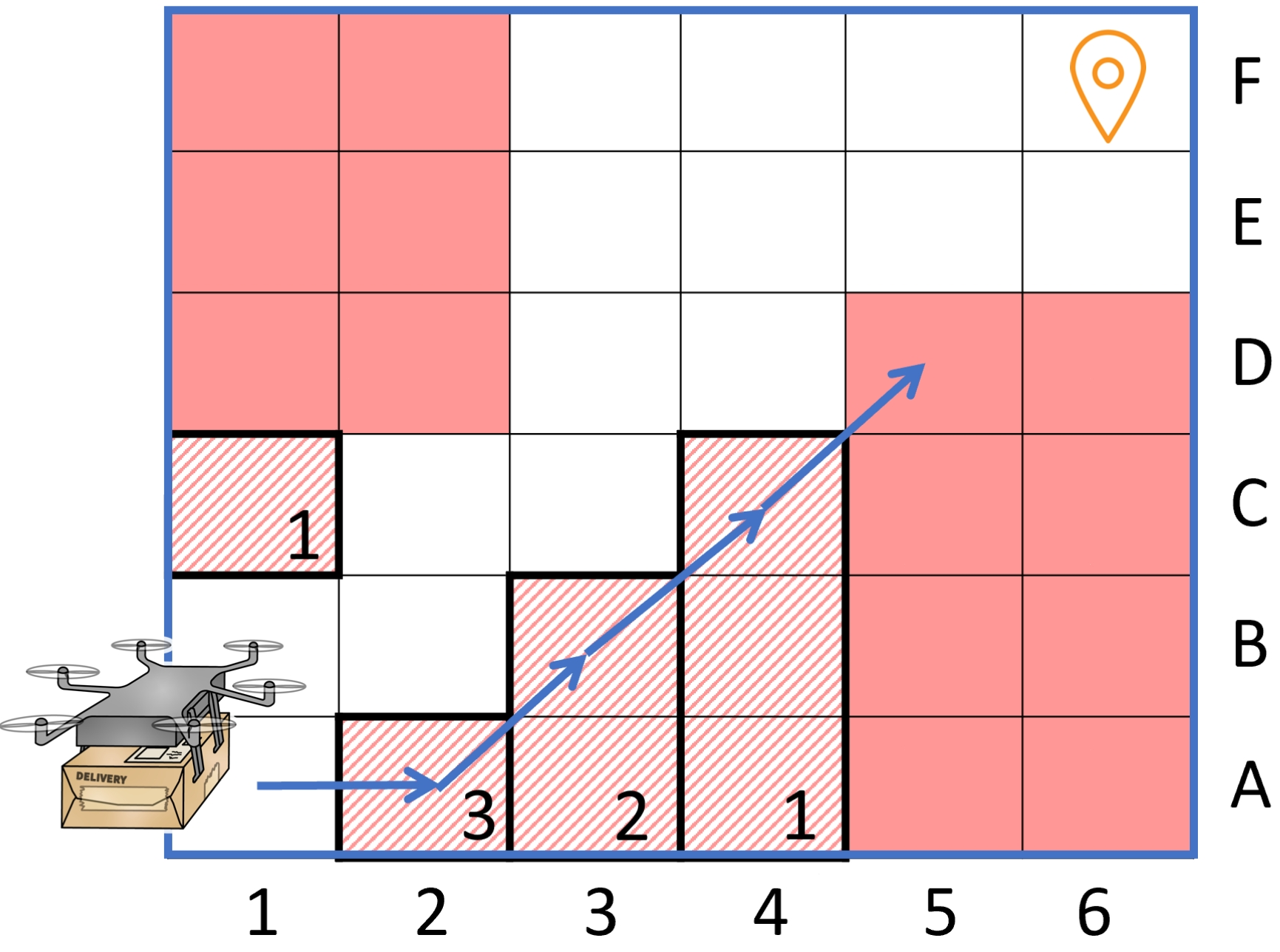
Example 1.  Figure 4 shows a discrete representation of the environment of a UAV, depicted as a two-dimensional grid. Figure 5 shows part of the MDP for this example, where the states correspond to the cells in the grid and the actions are the labels of the transitions that connect the states. The specification for this example is simple: Do not crash into a building. The red states, labeled 5A and 5B, indicate collisions of the UAV and a building, and thus violations of the safety specification.

The agent’s actions label the edges: north (N), east (E), south (S), and west (W). The outcome of an action is uncertain due to the southwest wind, captured by the probabilistic transition function. For example, if the UAV chooses Action N in Cell 4A, it will move to Cell 4B with probability $p$ and to Cell 5B with probability $1–p$.

Deterministic models.  MDP models represent the environment probabilistically. Using deterministic models, one can prevent unsafe behavior regardless of the behavior of the environment by adopting a worst-case view of its behavior. One reason to use such a deterministic model is that not enough data may be available to derive probabilities. Adversarial interaction between the environment and the agent can be modeled as a two-player game, where the next state is determined by the actions chosen by both the agent player and the environment player. By removing the probabilities from the edges and replacing them with the environment’s choices, we can transform an MDP into a two-player game.

Example 2.  Figure 6 depicts the two-player game graph derived from the MDP in Figure 5. The agent-player first selects an action, followed by the environment choosing its action. These decisions determine the subsequent state. For instance, when the agent selects Action N from Cell 3A, the environment can either move the UAV to Cell 3B by choosing Action N’ or to Cell 4B by selecting Action NE’.

States and features.  The rigor required to compute shields affects the scalability of the approach. Fortunately, shields can often be computed using models with a reduced feature space. By disregarding any features irrelevant to safety, the original model can be pruned to a much smaller model.¹⁹ In the UAV example, such features may include temperature or the designated goal position. Retaining the safety-relevant dynamics of the environment allows the use of model-based techniques to compute the shield, even when the performance-optimal policy cannot be computed with these model-based techniques.

Safety guarantees.  There is a rich body of literature on how to express properties of systems, for instance, using logics such as linear temporal logic.⁸ Shielding is typically used to enforce safety properties, which state that something bad never happens. In the UAV setting, a safety property could state, “The UAV never collides with another moving or static obstacle.” Safety properties can also encompass temporal aspects, such as “The UAV must reach the target within 30 minutes.”

For this article, it suffices to note that such properties can be converted to automata and combined with the model via standard product constructions.⁸ Without loss of generality, we can assume that the resulting model has at least one unsafe state that indicates a violation of the safety guarantee. A shield with absolute safety guarantees ensures that such an unsafe state is never visited, thereby ensuring that no safety property is violated.

Shield computation.  The specification of the safety properties that the RL agent must fulfill can easily be converted into a specification for the shield: The shield must 1) ensure that the agent satisfies the safety specification, and 2) allow the agent to select any action that is safe for any future actions of the environment. These requirements can be met by solving a safety game on the model of the environment. Solving a safety game involves computing a non-deterministic strategy that defines, for each state, all actions the agent can choose to ensure that an unsafe state is never reached. The methods for solving safety games are well established.⁸ We call a state dangerous if there exist actions that the environment may choose in the future such that visiting an unsafe state becomes unavoidable, regardless of the actions the agent takes. Vice-versa, a state is safe if it is not dangerous: The agent can always avoid an unsafe state, no matter what the environment does. In game theory, the set of safe states is referred to as the winning region. This set is inductive, meaning that from any safe state, the agent can select an action that leads to another safe state, regardless of the choice taken by the environment. A shield ensures that the agent remains within the winning region by permitting only those actions that maintain this condition.

The set of dangerous states can be computed recursively by a backward traversal of the graph in time linear in its size. The algorithm keeps a set of dangerous states, which is initialized to the set of unsafe states. At each step, the algorithm adds all states from which, regardless of the action of the agent, there is an environment action that leads to a dangerous state. From such states, the environment can enforce that a dangerous state will be visited. The algorithm continues until a fixpoint is reached.

Example 3.  Figure 7 illustrates the safe (white), the dangerous (shaded red), and the unsafe (red) states for the UAV example. The boxes surrounding the dangerous states illustrate the intermediate steps of the algorithm for computing the winning region. Initially, the dangerous states in Box 1 are identified, representing states from which the environment can force a transition to an unsafe state in a single step. For instance (referring back to Figure 6), State 4A is dangerous because both for Action N and for Action E, the environment can choose to visit to State 5B, which is an unsafe state. Similarly, the dangerous states in Box 2 and Box 3 represent states from which the environment can force a transition to an unsafe state in two and three steps, respectively.

Finite horizons.  In the previous section, we required the agent to remain in the winning region forever. This requirement is not applicable to all probabilistic systems. Since events that happen with a very low probability at any time will happen eventually with probability one, given enough time, restricting ourselves to an infinite horizon would make the definition (almost) as conservative as shields with absolute safety guarantees. Consequently, we often consider a finite horizon of $h$ steps. The horizon can be chosen to be the mission time, the expected battery life, or the time that a safety procedure requires.

Permissive policies versus probabilistic shields.  Lifting shielding toward probabilistic guarantees comes with some design choices, which we illustrate with the following example.

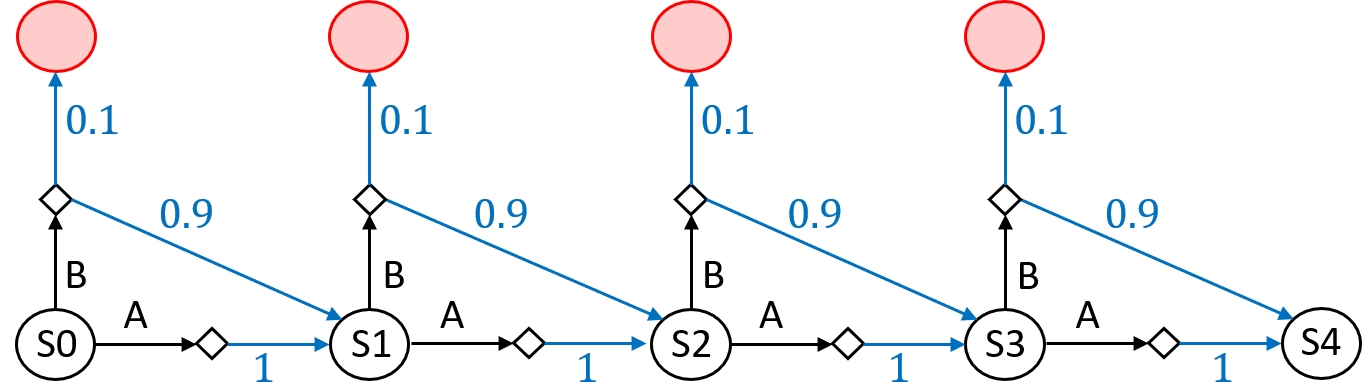
Example 4.  Consider the MDP shown in Figure 8. As a safety specification, we want to ensure that the probability of reaching a bad (red) state does not exceed $0.1$ within, say, four steps. This specification is satisfied by any policy that takes action $B$ at most once.

The design choice can be exemplified by the following Gedankenexperiment: When an agent is in state $S1$, should the shield allow taking action $B$? Option 1 is to allow taking action $B$, as afterward always taking action $A$ will ensure that the specification is satisfied. Option 2 is to only allow taking action $B$ if the agent did not choose action $B$ in state $S0$. Option 3 is to not allow taking action $B$.

Option 2 is the perspective that permissive policies^11,22 take. Permissive schedulers tend to be conservative and hard to compute. They prevent actions based on previously taken risks, even when those risks were successfully averted. We focus on Option 1, which aligns with the idea discussed in the previous section: A shield allows any action for which it can keep ensuring that it is possible to satisfy a given specification. The clear downside of following Option 1 is best observed in the previous example: The shield will, in every step, allow taking action $B$, and thus, a shielded policy may take $B$ in every step and thereby not meet the given specification. Finally, Option 3 is feasible in the given MDP but generally leads to situations in which every action is prevented, even when there are safe policies.

Probabilistic shields.  In line with Option 1, we call an action safe if, after taking that action, the minimal probability of reaching an unsafe state within $h$ steps is at most $\epsilon$. Otherwise, an action is called unsafe. The winning region is the set of all states for which at least one safe action exists.

Shield computation.  To construct the shield, we must compute the probability that something bad happens within $h$ steps, assuming that the agent acts optimally in terms of safety in the future. Thus, we are interested in the minimal reachability probabilities across all possible behaviors of the shielded agent. If the exact computation of these probabilities is not feasible, we must obtain upper bounds.

Computing (upper bounds on) the optimal reachability probability in an MDP is a standard problem, often also referred to as the stochastic shortest path problem.³ This task requires solving a dynamic program. The minimal reachability probability when taking action $a$ in state $s$ is the expected minimal reachability probability over the successors. The set of dangerous states is then determined by computing the minimal probability of reaching a bad state within $h$ steps.

The resulting dynamic program can be solved in time linear in the number of states, actions, and the horizon. As mentioned above, similar queries have also been defined for more intricate temporal properties and can be solved via adaptions of value iteration, policy iteration, or linear programming.

Example 5.  The following equations give a fragment of a dynamic program to define the minimal probability to reach bad states in Figure 5, where $x_{ij,h}$ describes the minimum probability to reach a bad state from Cell $\langle i,j\rangle$ within $h$ steps:

Given the winning region and the set of safe actions, the shield can be directly deployed. In case a state outside of the winning region is entered during runtime, a fallback strategy needs to be defined, such as selecting a predefined action (for example, braking or landing), or allowing only the safest possible action.

Collision avoidance with absolute safety guarantees.  Figure 9 illustrates the grid world for the first demonstration. The agent’s task is to control UAV-1 to deliver packages to a designated target position. The safety objective is to avoid collisions with UAV-2 (framed in red) and buildings.

We model UAV-2 adversarially, assuming that it actively tries to collide with UAV-1. This way, the shield’s safety guarantees hold regardless of the behavior of UAV-2 (see earlier section, “Shielding with Absolute Safety Guarantees”). We deploy shielded and unshielded RL to search for an optimal and safe policy to deliver the package. During training, the agent is rewarded when reaching the goal and receives a negative reward for violating safety. Additionally, it receives a small negative reward for each step taken.

Results.  The learning results are illustrated in Figure 10. The orange curves represent the results for unshielded learning, while the blue curves show the results for shielded learning with absolute safety guarantees. Figure 10a reports the reward, and Figure 10b shows the accumulated safety violations, both averaged over five runs. In this example, shielding clearly enhances learning performance. The challenging part of this learning task is avoiding collisions with UAV-2. Since the shield handles this aspect, the shielded agent quickly learns to complete the package delivery efficiently. While the unshielded agent eventually learns to avoid collisions and to achieve a similar expected reward, the shielded agent never violates safety and converges in a fraction of the time.

Collision avoidance with probabilistic safety guarantees.  The grid world for the second demonstration is depicted in Figure 11. In this example, the UAV has to deliver a package without crashing into a building, while wind affects its movement. The wind direction is modeled individually for each cell, with a 5% probability that the wind displaces the UAV in its direction. We compute shields that provide probabilistic safety guarantees (see earlier section, “Shielding with Probablistic Guarantees”), using a finite horizon of 20 time steps and the probability thresholds $\epsilon \in \{0.00,0.03,0.05\}$, where $\epsilon$ limits the risk the agent is allowed to take. As before, we compare unshielded and shielded RL for finding a policy for delivering packages, using a similar reward function.

Results.  The orange curves in Figure 12 depict the reward and the number of safety violations observed during training without a shield. The blue curves depict the same metrics when shields with different probability thresholds are applied. As expected, the lower $\epsilon$ is, the fewer safety violations occur. Interestingly, when using either shield that allows the agent to take some risk, the agent learns faster and achieves a higher reward compared to using no shield or a shield that completely forbids taking risks.

Figure 11 illustrates the learned paths for the different learning settings. The unshielded agent learns to take the shortest and narrowest path (orange), which involves a relatively high risk of colliding with a building. In contrast, the shielded agents take longer but safer routes. The shields with $\epsilon =0.03$ and $\epsilon =0.05$ allow the path between the buildings (light blue), enforcing only a slightly larger distance from the buildings. Thus, most of the agent’s flexibility in choosing the path to the target is maintained, while its search space is reduced by prohibiting too risky routes. The longest path (dark blue), which circumnavigates the building, is taken using the shield with $\epsilon =0.00$, resulting in a lower final reward.

Partially observable environments.  So far, we have considered fully observable environments, where the shield (and the agent) knows the precise state. This assumption may be unrealistic. A standard approach is to consider partially observable environments, where only a part of the state can be observed. Shields are then computed from partially observable Markov decision processes (POMDPs). A challenge for these models is that computing policies is hard or even undecidable.²⁶ Fortunately, conservative shields can potentially be computed by under-approximating the safe actions. Such shields can be constructed for non-trivial examples, guaranteeing safety and potentially improving the empirical learning rate.⁷

Continuous state and action spaces.  Shielding can be extended to systems with continuous state and action spaces. Using continuous systems increases the theoretical complexity and tractability of computing shields. Yet, several papers address this extended problem. For example, Fisac et al.¹⁴ provide a Bayesian method to provide safety guarantees for robot systems. Kochdumper et al.²³ propose a post-shielding approach for cyber-physical systems with nonlinear dynamics using zonotopes, and David et al.¹⁰ proposed a pre-shielding approach for systems with continuous time. Brorholt et al.⁶ present an approach to shielding based on discretization, while Rodriguez et al.³⁶ present a method based on properties written in LTL modulo theories, which allows reasoning over non-Boolean domains. Simplex-based approaches for guaranteed safety in a continuous setting have also been considered.^21,27,32

Multi-agent systems.  Shielding multi-agent systems is difficult, as most verification problems are undecidable in a distributed setting. Nevertheless, shields for multi-agent systems have been introduced using runtime verification results, in both centralized and decentralized settings.^4,12,28

Beyond safety.  Safety properties require that something bad never happens; that is, any violation of a safety property consists of a finite “bad” trace. This class is relatively broad, encompassing invariants, such as “a collision never happens,” as well as bounded properties, such as “every request must be answered within five time units.” However, various unbounded properties are not safety properties. For example, consider that a UAV should eventually reach its destination. Properties for which no finite bad trace can, by itself, demonstrate that the property is violated are called liveness properties.⁸ Under certain assumptions, a liveness property can be ensured by a shield that merely prevents an agent from entering a state in which satisfying the property becomes impossible. For instance, a UAV should not drain its battery before reaching its destination, as doing so would prevent the UAV from ever getting there. One such assumption could be that the agent follows an $\epsilon$-greedy strategy,⁷ ensuring that it will eventually explore any unshielded action. In the absence of such assumptions about the agent’s behavior, shielding becomes more challenging, as the shield must enforce specific actions to ensure the satisfaction of the liveness property. The main question is when the shield should interfere. Specifically, at any point in time, if the shield intervenes to satisfy the liveness property, this intervention may be premature, as the agent might have satisfied the property on its own at some later point in time. One possible approach to decide when to interfere employs quantitative methods, assigning costs to violations of a property and to the shield’s interference.²

Acknowledgments.  We thank Chao Wang and Robert Koenighofer for the inspiration and the work on the initial formulation of shields; Ruediger Ehlers for his great contributions to shields for reinforcement learning; Ufuk Topcu for many interesting ideas; our many other collaborators and students for ideas, discussions, ideas, and implementations; and Dejan Nickovic, Benedikt Maderbacher, and the anonymous reviewers for many comments that improved the article. Illustrations by Theresa Dachauer.

This research was funded in whole, or in part, by the Austrian Science Fund (FWF) [10.55776/S114] and [10.55776/W1255], by the State Government of Styria, Austria – Department Zukunftsfonds Steiermark, via the ERC Starting Grant 101077178 (DEUCE), and via the NWO Veni Grant 222.147 (ProMiSe). For the purpose of open access, the author has applied a CC BY public copyright license to any Author Accepted Manuscript version arising from this submission.

To access the Appendix for this article, please visit https://dl.acm.org/doi/10.1145/3715958 and click on Supplemental Material.