Programming is both an enjoyable and a difficult task. A seemingly small slip can introduce a serious error or create a security vulnerability. The need for, and importance of, program correctness was recognized early in the modern development of computing.
Algorithms, on which programs are built, arose in the ancient world (and are commonly attributed to the Greeks). The word verification dates only to Medieval Latin; however, when Euclid introduced his algorithm for the greatest common divisor centuries earlier, he provided a proof sketch based on what we would today call inductive reasoning.13 With the introduction of computers and programming, verification has become an art of its own.
Key Insights
Classical program verification techniques do not scale easily to large and complex programs. As a consequence, although most software is tested, it is not formally verified and may be buggy and vulnerable to security attacks.
- Self-certification is a lightweight, alternative approach to correctness. Unlike testing, self-certification establishes the correctness of every individual program execution by generating and checking certificates.
Self-certification has been discovered independently in different contexts. This article aims to find unity in this diversity, to encourage the use of certification in new domains, and to point to fundamental open questions.
In its classical form, the program verification question is designed to prove that every potential execution of a program meets a specification. The famous “Halting Problem” is a program verification question, as it asks whether a program terminates on a specific input. Even in this restricted form, Turing showed that the question is undecidable, establishing the inherent difficulty of verification.43
Decades of subsequent research have led to the development of two main verification techniques: deductive proofs and model checking. Deductive proofs are typically developed manually, using automated proof assistants that ease the construction and checking of proofs. On the other hand, model-checking algorithms fully automate program behavior analysis by systematically exploring the entire program state space. These techniques can establish full correctness in principle; in practice, however, the construction of a deductive proof requires considerable effort and expertise, while model checking faces serious scalability limitations due to state explosion.
These limitations have led to the development of “lightweight” methods. Static program-analysis tools, built around the theory of abstract interpretation,10 are routinely used to analyze multimillion-line programs. Scalable analyzers typically check for specific vulnerabilities, such as arithmetic overflow or buffer overrun, rather than full correctness. Runtime verification (RV)17 is used to monitor the execution of long-running concurrent and distributed systems. RV methods are scalable but are focused on detecting specific pitfalls, such as race conditions and failures of serializability. Program testing is the most common method for checking program behavior. Testing, however, validates program behavior only for the tested cases, providing no guarantees of correct behavior for the untested ones. In Dijkstra’s famous words, “program testing can be used very effectively to show the presence of bugs but never to show their absence.”11
Lightweight methods are thus restricted in scope and do not provide for full verification. The undecidability of verification is a fundamental barrier, implying that any sound and automated analysis method may only produce approximate results.
The irony is that because of these limitations, the programs we rely upon every day—those arguably most in need of careful verification—go largely unverified. Operating systems, device controllers, Web browsers, banking systems, and Internet services are rarely formally verified. We have become so inured to this fact that the discovery of bugs and security failures in software is a commonplace, even expected, occurrence.
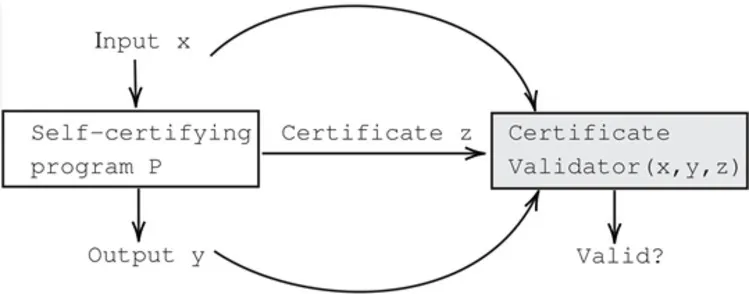
Self-certification, explored here, is an alternative to daunting verification or capricious testing. A self-certifying program is designed to produce a correctness justification, called a “certificate,” on every execution. The certificate is in a form that can be validated easily and independently of the generating program and its execution environment. Independence is necessary as the program producing the certificate is unverified and thus may produce an invalid certificate. Ease of validation implies that the certificate validator is typically simple enough to be formally verified in the classical sense. This process is illustrated in the figure.
Self-certification improves on testing by checking every program execution for correctness. It improves on RV by guaranteeing full correctness. In practice, the safety net of the certification mechanism gives programmers freedom to introduce intricate data structures or highly optimized code into the source program that would be challenging to verify in the classical sense. Although certification is weaker than full-fledged formal verification, it is much simpler to apply in practice. One may informally view self-certification as a “selfish” verification method, one that fully validates only the program runs that actually occur.
In practice, self-certification can be viewed as transferring trust from a complex, unverified program to a simple, verified validator. A valid certificate implies that the execution meets the specification. An invalid certificate indicates either a program error or a mistake in forming the certificate. The first is, of course, a serious issue, but so is the second, as it suggests that the programmer has an incomplete understanding of the working of a program or its intended purpose.
The central idea behind self-certification is “checking the result,” something we have all done since grade school. For example, check the claimed answer c for a − b by verifying that c + b equals a. For a less trivial example, consider the task of sorting a sequence of numbers. Any sorting program must transform an input sequence a into an output sequence b of the same length, such that (1) b is a permutation of a, and (2) b is nondecreasing; that is, b (i) ≤ b (i + 1) for every i in [1..(N − 1)], where N is the length of the sequence.
Although standard sorting algorithms have formal correctness proofs, their implementations may contain subtle programming errors. Thus, it is necessary to check whether the desired properties hold for every execution of a sorting program. Although property (2) can be checked in linear time, checking property (1) is essentially as difficult as sorting. Now suppose the sorting program provides an auxiliary output in the form of a function π from [1..N] to [1..N]. For π to be a valid certificate for property (1), it must be the case that π is a permutation of the indices [1..N], and that b (i) = a(π(i)) for every index i. Both properties can be checked in linear time.
This example (also discussed in Wasserman and Blum47) shows that a specification could have several types of certificates with different trade-offs between the cost of generation and the cost of checking. As a general principle, a certificate should be generated with limited additional effort and checked easily and efficiently.
Crucially, a certificate is defined only in terms of the specification, in this case, sorting. Hence, a single (verified) validator suffices to check the correctness of every self-certifying implementation of any sorting algorithm. Subsequently, we will see certificates for specifications of higher complexity that are NP-complete, PSPACE-complete, or even undecidable.
Self-certification is not a new idea. It appears to have been discovered independently in diverse contexts, including graph algorithms, program verification, compiler design, and distributed systems. An early instance is a series of articles by Manuel Blum and co-authors, starting in 1988.4,5,6,47 These articles proposed the notion of a “simple checker” (sometimes referred to as a “program checker”). In their formulation, a checker is an efficient probabilistic program that accepts or rejects a result of the program it checks. Some checkers only have access to the input and output values while, in other cases, the program is modified to generate auxiliary certificates. In this formulation, certification is not absolute but is provided only with high confidence.
This early work is primarily concerned with designing checkers for efficient but tricky algorithms, for problems in group theory, and for questions such as graph isomorphism. By the late 1990s, the idea of self-certification had been extended to other domains. Work by Mehlhorn (with colleagues) applied certification to implementations of efficient but complex graph algorithms, such as for planarity testing.28 Certification as applied to program translators (for example, optimizing compilers) was developed in Cimatti et al.,8 with the notion of translation validation appearing shortly afterwards in Pnueli et al.38 Proof Carrying Code35 is a related but different concept.
Two excellent surveys28,47 describe certification for algorithmic questions. This article builds on those surveys, describing applications of certification to logic, verification, and compiler design. A major objective is to find unity in this diversity: to formulate certification in a way that brings out its essential features while retaining its generality and scope. Another important goal is to inspire the use of certification in new domains. Our analysis also points to fundamental questions that do not yet have a satisfactory answer: What constitutes a good certificate? Can every specification be certified? What are the intrinsic costs of certificate generation and validation? We hope this article will spur progress in understanding, studying, and resolving these questions.
A Self-Certifying Bubblesort
To illustrate self-certification, we show how to augment the well-known bubblesort algorithm to produce a certificate and how to design a formally validated certificate checker for sorting. As readers will recall, bubblesort divides the input list of numbers into two parts. The right-hand part (initially empty) is sorted, while the value of each element of the left-hand part (initially the input list) is upper-bounded by the values of elements in the right-hand part. A single pass moves the maximum entry of the left part to the right part, making progress while reestablishing their relationship. This pass is repeated until the left part is empty.
Pseudocode for a certificate-generating bubblesort is presented in Algorithm 1, with lists encoded as arrays. For array X, the swap(X, i, j) action exchanges the values of the elements X [i] and X [ j]. If the declaration of the array π and the references to it in Lines 2 and 7 are ignored, this is a typical unoptimized bubblesort. The array π holds the certificate, that is, the permutation of a’s elements as they are in b. Initially we have b = a; thus, π is the identity permutation. The inner loop in Lines 4–9 moves the maximum entry of the left part to its correct location in the (sorted) right part and modifies the permutation array π accordingly.
Algorithm 1. A self-certifying bubblesort algorithm.
input: integer N : N >0
input: array a of N integers
output: array b of N integers
output: array π of N integers
1 b ← a
2 π ← [1, . . . , N ]
3 for i ← N − 1 downto 1 do
4 for j ← 1 to i do
5 if b [ j ] > b [ j + 1] then
6 swap(b, j, j + 1)
7 swap(π, j, j + 1)
8 end
9 end
10 endTo determine the correctness of an execution of a sorting program for input list a, output list b, and a claimed certificate π, a validator must check three properties:
(P1) The elements of b are sorted, that is, arranged in non-decreasing order,
(P2)b (i) = a (π(i)) for all i in [1..N], and
(P3) π is a permutation on [1..N], that is:
(P3.1) π has co-domain [1..N], and
(P3.2) π [i] = π [ j] if, and only if, i = j .
Properties (P1), (P2), and (P3.1) are easily checked in linear time. To check (P3.2) in linear time, we use an auxiliary Boolean array M (for “Mark”) that is initially all unmarked. While scanning the i’th entry of π, we mark the M-entry for π [i]; if it is already marked, then π is not a bijection.
The validator is described in Algorithm 2. It was formally verified using the Ivy29 proof assistant. The first loop checks for a violation of (P1). The second loop checks (P2) and (P3): The first disjunct on line 8 checks (P3.1), the second checks (P2), and the third checks (P3.2). The loops, separated for clarity, are both linear in N.
Algorithm 2: Checking a sorting certificate in linear time.
input: N,a,b,π as above
output: ERROR or VALID
1 for j ← 1 to N − 1 do
2. if b [ j ] > b [ j + 1] then
3. return ERROR
4 end
5 end
6 M ← an array of N booleans, all false
7 for i ← 1 to N do
8 if π [i] ∉ [1..N ] or a [π [i]] ≠ b [i] or M [π [i]] then
9 return ERROR
10 else
11 M [π [i]] ← true
12 end
13 end
14 return VALIDA brief history of verification. The deductive approach to program verification was originated by Goldstine-von Neumann46 and Turing44 in the late 1940s and early 1950s. These informal methods for verifying sequential programs were formalized by Floyd in 1962 (published in 1967,16 who attributes his ideas to unpublished work by Perlis and Gorn), and by Hoare in 1969.19 A deductive proof consists of invariance assertions, which define stable properties of program state, and ranking arguments, which establish convergence to desired subsets of program states. Pnueli and Manna showed how to extend invariance and ranking arguments to prove the correctness of reactive non-terminating programs, such as device controllers and network protocols.25,26
A program may also be verified through a process of stepwise refinement. Here, an initial abstract program forms the specification. This program is systematically converted to a concrete program with a desired level of efficiency or detail. At each step of transformation, it is necessary to show that every behavior of the transformed program is a behavior of the original program, a relationship known as refinement. The refinement property is proved through an inductive correspondence relation between the state spaces of the two programs, known as a (bi)simulation.20,30,31 Mechanized proof assistants (such as Coq, PVS, Isabelle/HOL, and ACL2) support the construction and checking of proofs. Yet, the major burden of formulating a proof remains on the human verifier. As a result, the construction of proofs of even moderately sized programs may require considerable time, effort, and mathematical expertise. As a concrete data point, a proof of a 1,000-line compiler optimization required a 10,000-line Coq proof script and more than a person-year of expert effort.48 Such numbers are typical. This enormous effort is balanced by the considerable benefit of having established, once and for all, that a program behaves as expected in every case.
An important class of programs is that of finite-state circuits and network protocols. Such programs typically have several concurrently active components or threads, which considerably increases the difficulty of formulating a deductive proof argument. Model checking decides correctness entirely algorithmically, by systematically and exhaustively analyzing the finite state space.9,39 Model checking works remarkably well in many cases. Its fundamental challenge is that of state explosion: A program with m concurrently executing components, with two states each, has a potential reachable state space of size 2m. State explosion can be tamed to an extent by the use of compact data structures and abstraction methods but, in general, it limits the practical applicability of model checking.
Examples of Self-Certification
Before moving to a mathematical formulation of self-certification, it is instructive to look at examples of certification from various domains. Earlier surveys6,28,47 cover certification for algorithmic questions in group theory and graph theory. In this section, we discuss certification for questions in logic, verification, distributed systems, and program transformation, several of which are beyond NP in complexity, while some are even undecidable.
Logic. We give two examples of certificates from logic. The first is for the prototypical NP-complete problem: Boolean Satisfiability (SAT). A Boolean formula is in SAT if it is satisfiable, that is, if there is an assignment of Boolean values to the variables of the formula under which the formula evaluates to true.
For a “Yes” answer to SAT, a satisfying assignment forms a valid certificate. The format of a certificate is that of an assignment of values to variables. A certificate in this format is valid if the formula evaluates to true under the assignment provided by the certificate. The past three decades have seen remarkable advances in SAT-solving in practice. SAT solvers are implemented with highly optimized C or C++ code, which raises concerns about the presence of subtle bugs. Although the research community has developed some formally verified solvers, commonly used solvers are not formally verified. Nonetheless, all produce a satisfying assignment to certify a Yes answer.
What about formulas that are not satisfiable? A formula φ is unsatisfiable if, and only if, its negation ¬ is valid (that is, if ¬ is true for all assignments.) The validity of ¬can be established through a deductive proof, which acts as a certificate for the unsatisfiability of . While the proof length cannot be guaranteed to be polynomial in the length of (which would imply NP=coNP), it is easy to check a claimed proof by inspecting each inference step. There are several proof systems to choose from; many SAT solvers produce unsatisfiability proofs in the DRAT format.18
The second example is the extension of propositional logic with Boolean quantification. A Quantified Boolean formula (QBF), as the name suggests, allows nested application of the existential (∃) and universal (∀) quantification operators to propositional formulas. QBF satisfiability is the prototypical PSPACE-complete problem.
Consider a quantified formula of the shape (∀x(∃y (x, y))), where the inner “kernel” is quantifier-free. This formula is either true or false, as it has no free variables. If it is true, then for every Boolean value a for x, there is a Boolean value b for y such that (a, b) is true. Unlike SAT, a single assignment cannot serve as a certificate. Instead, one needs an “assignment generator” to produce an appropriate value of y for each value of x. This is known as a Skolem function, after the logician Thoralf Skolem. Given a Skolem function F, the QBF formula can be rewritten to (∀x (x, F (x))). A Skolem function can be viewed as a Boolean circuit with input x and output y. A certificate of correctness is thus the Skolem function F as a Boolean circuit, along with a deductive proof for the validity of the quantifier-free Boolean formula (x, F (x)), which is generated as for the SAT problem.
Formulas with a deeper alternation of quantifiers require a Skolem function for each existentially quantified variable. For instance, the certificate for (∀x1(∃y1(∀x2(∃y2 (x1,x2,y1,y2))))) consists of a Skolem function F1 mapping x1 to y1, a Skolem function F2 mapping x1 and x2 to y2, and a validity proof for (x1,x2,F1 (x1), F2 (x1,x2)).
This discussion is based on the traditional notion of a proof as a static object. Complexity theorists have fruitfully extended the notion of a proof to that of an interactive randomized protocol (IP), where a Prover and Verifier engage, informally speaking, in a question-and-answer session before the Verifier reaches a decision on the validity of a claim made by the Prover. Shamir42 shows that IP=PSPACE; that is, that all PSPACE-questions have short interactive proofs.
A fascinating offshoot is the notion of a zero-knowledge (ZK) proof. Here, the interaction is such that a verifier is convinced (with high probability) of the truth of the Prover’s claim without learning anything about why it is true. Non-interactive variants of ZK-IP proofs, known by various acronyms (SNARKs, STARKs, …), are used for applications where, for instance, one party wants to offer an algorithm as a service while keeping secret certain aspects (for example, Ben-Sasson et al.2). Succinct ZK proofs act as certificates that, in addition, hide information.
Model checking. Model checking in its pure form9,39 is a fully automatic process for verifying sophisticated temporal properties of finite-state machines. Model-checking methods systematically explore the state space of the machine, using either graph algorithms or fixed-point calculations.
It is perhaps easiest to appreciate the automata-theoretic approach to model checking.45 Here, the machine is viewed as a generator of words, and the negated property as an acceptor of words, both being represented as automata over (infinite) words. The machine satisfies the property if the intersection of these two automata languages is empty; thus, model checking reduces to a language emptiness test over finite automata.
If the property is violated, there must be a word that is accepted by the intersection automaton; this word is a certificate that explains the violation. This certificate is commonly known as a counterexample. Historically, the ability to generate counterexamples was a major factor in the widespread adoption of model checking.
What if the property holds (that is, the intersection automaton has an empty language)? The authors (with collaborators) show in Namjoshi32 and Peled et al.37 that, in this case, one can instrument the model-checking algorithm to extract a deductive proof that justifies correctness.
The extracted deductive proof is expressed in terms of the central concepts of invariance and ranking introduced earlier in this article. Deductive proof certificates can be generated for both linear and branching-time temporal specifications, and from a variety of model-checking algorithms. Several software model-checking tools produce deductive proofs of correctness (and violation) in a well-defined and machine-checkable format of a “verification witness.”3
Interestingly, for branching-time logics, it is possible to produce a deductive proof of failure. Model checking can also be framed as an infinite game in an arena defined by the product of the program and a (branching) property automaton.12 The opponent makes the universal choices in this game, while the player makes the existential choices. The property holds if and only if the player has a winning strategy. The deductive proof represents a winning strategy for the player, expressed compactly in the form of invariants and ranking functions. As branching-time logics are closed under negation, a program that fails to satisfy a property φ must necessarily satisfy the negated property ¬. A failure proof thus represents a winning strategy for the opponent in the model-checking game and can also be expressed in terms of invariants and ranking functions.32
Conceptually, the notion of a proof-generating model checker neatly links the algorithmic and deductive approaches to program verification. In practice, it guards against the danger that a production model checker, which typically runs into the hundreds of thousands of lines of code, may have a serious bug that causes it to incorrectly miss reporting a property violation.
Graph algorithms. We present two examples of certificates for graph algorithms. For the NP-complete Hamiltonian Path problem, the certificate is a path. A claimed certificate is valid if the path has the Hamiltonian property. Indeed (by definition) for any language in NP, every word in the language has a polynomial-sized certificate that can be validated in polynomial time. A different and useful way of seeing this is via Fagin’s elegant characterization of NP as those properties expressible in existential second-order logic,14 that is, as (∃R : (R)) where R is a set of relation variables and is a first-order formula.
This formulation compactly represents many graph problems, including Hamiltonian Path. The certificate is then an instantiation of the variables in R, while validation is the process of checking that is true for a claimed certificate R.
Our second example is that of graph planarity, a problem that is solvable in polynomial time. For a positive answer, the certificate is an embedding of the graph in the plane. For a negative answer, the certificate is an embedding in the input graph of the “forbidden” graphs K5 (complete graph on five vertices) or K3,3 (complete bipartite graph with three vertices on each side). Such an embedding certifies non-planarity by Kuratowski’s theorem.7 Checking a given embedding is simpler than verifying an implementation of a planarity algorithm, such as the Hopcroft-Tarjan method.
Here, we would like to emphasize once again that the focus of self-certification is on the correctness of implementations. The underlying algorithms are usually stated in mathematical notation and have correctness proofs. The difficulty arises with validating their implementations. A programmer must turn the algorithm into an implementation, making choices about representations of data structures, expanding computation steps, and possibly introducing optimizations to detect and solve special cases. Hence, the implementation differs from the algorithm and is harder to verify. Certification for graph algorithms was pioneered by Mehlhorn and collaborators and implemented in the LEDA package. The work in McConnell et al.28 describes the genesis of this work: It came about from the recognition that bugs in LEDA could go unnoticed unless there was a way to check each answer. LEDA contains checkers for several graph algorithms and for geometric algorithms such as computing triangulations.
An interesting question arising from the Hamiltonian Path example is the following: What is the certificate if the graph does not have a Hamiltonian Path? One option is to list all simple paths and check that they are not Hamiltonian, but this is neither concise nor elegant, and it raises other concerns: for example, how does one prove that all paths have been enumerated?
A possible answer is through a verified reduction to SAT. It is, in principle, possible to convert a negative answer to the Hamiltonian Path problem on a graph G to a certificate of the unsatisfiability of a Boolean formula r(G) obtained via a provably correct reduction r. We discuss reductions later in this article.
Distributed computing. The notion of certification is well-studied in the distributed computing literature, appearing under several formulations. We illustrate the central ideas through two examples.
Consider the problem of computing a maximal independent set (MIS) of nodes in a connected graph. An MIS is a subset S of the nodes such that every node v ∈ S has no neighbors in S, and every node v ∉ S has a neighbor in S. A distributed protocol computes an MIS by letting a node output “Yes” if it is in the set, and “No” otherwise. (An example is Luby’s well-known probabilistic protocol for MIS,23 where termination of each node is guaranteed with probability 1.) Once all nodes terminate, one can check locally whether the computed set is indeed an MIS. Consider a node v. If its output is “No” then one needs to check that v has some neighbor whose output is “Yes.” If the output of v is “Yes” then one needs to check that the output of every neighbor of v is “No.”
This example demonstrates that although MIS is a global property, it has a correctness certificate that can be locally checked, that is, where each node checks a property of its own output (and certificate) and that of its immediate neighbors.
Consider now the problem of computing a spanning tree in a connected graph. (See, for example, Lynch’s spanning tree protocols24). In most protocols, a terminating node knows its parent and can determine its children. The root, of course, has no parent. Protocols may be initiated at the leaves and work toward the root, or start from the root and go down the tree. For this exposition, assume that the protocol starts at a unique designated root. Assume further that each terminating (non-root) node outputs its parent. Then, checking that the protocol indeed computes a spanning tree requires checking that each non-root node has a parent connected to it and that the root, together with all nodes reachable from it, comprises all the nodes of the graph. Being a spanning tree is also a global property but, unlike in the MIS example, the assignment of parents does not suffice for a local test of correctness, as it is also necessary to compute reachability in the graph.
There is, however, a way to augment the parent information to form a locally checkable certificate. Let each node, in addition to its parent, output its level in the tree, with the root being level 0. This suffices for a local check: Each node at level k > 0 should have a parent to which it has an edge and is at level k − 1, and the (a priori designated) root is the single level-0 node, which, unless the graph is a singleton, has children.
Various aspects of locality have been studied in distributed computing. The research of local certificates focuses on runtime, efficiency, and communication costs of certification.
The work in Naor and Stockmeyer34 formally defines locality in the context of identifying the class of computations that can be performed “locally” (that is, within a given fixed distance of each node) in constant time. It studies the class and describes some rather nontrivial members of it. A nice survey of local certification and self-stabilization is in Feuilloley,15 which studies the certificate size of a protocol as the size of the smallest certificate that permits local checking of the protocol. The work in Korman et al.21 establishes that every predicate on network configuration can be certified by a certificate of size Θ(n2) (where n is the number of nodes). This certificate consists of the adjacency matrix of the graph distributed to each node. Each node verifies that its own result is consistent with this certificate and that all neighboring nodes have the same certificate. There are cases where much shorter certificates exist.
We conclude this section of distributed systems by pointing out a particular class of systems whose computation is inherently self-certifying, namely, those whose goal is to establish consensus and carry the proofs of others’ computations. This is often carried out by digital signatures when the parties are not to be trusted. In the Byzantine Generals algorithms for consensus, the goal is to establish that every honest player will eventually know that every honest player . . . will eventually know that the decision is some value d. Thus, every (honest) player that reaches a decision has concrete information (that is, certificates) about the state of other players that allows it to reach the decision. These certificates are often digitally signed to prevent dishonest players from tampering with or forging them. While the protocol may not explicitly publish these certificates, they usually can be produced by adding a “publish all certificates” action to each participant.
Program transformations. A compiler converts a program written in a source programming language to an executable form. In its typical form, the front end of a compiler transforms a source program into a simpler intermediate representation (IR), then a sequence of IR-to-IR transformations are applied to “optimize” execution, followed by a back-end process that transforms the IR into an executable form. Production-quality compilers are very large programs. For example, the popular GCC compilation framework has more than 10 million lines of code. Despite considerable care in programming, errors inevitably creep in.
Compilation errors are difficult to detect, as the transformations convert a human-understandable source program to a barely recognizable target executable; moreover, an error may result in a difference in behavior between source and target programs only on a vanishingly small proportion of inputs. Several ingenious compiler testing methods have been developed but, by the nature of testing, those may miss errors.
Compiler correctness has been, for these reasons, a major verification challenge since the 1960s. The classical approach is to develop a machine-checked deductive proof of correctness for each program transformation; notable examples include Leroy22 and McCarthy and Painter.27 Proofs of this sort require considerable time, effort, and expertise. For instance, a well-documented effort at proving a 1,000-line transformation (to static single assignment, or SSA, form) for the LLVM compilation system required roughly 10,000 lines of proof script for the Coq proof assistant and more than a person-year of expert effort.48
The correctness criterion for all transformations is the same: a transformation should preserve input-output behavior. That is, given the same sequence of inputs, the original and optimized program should produce the same sequence of outputs. (This criterion is complicated slightly by the presence of potentially undefined behavior in the source program, such as a division by zero or a buffer overrun. In those cases, the target program may replace the undefined behavior with a specific action, such as halting, if allowed by the language semantics.) In its essence, compiler correctness is a program equivalence question, which is undecidable in general.
In the 1970s, Samet41 developed methods to check for equivalence of programs related by compiler transformations. This approach was independently rediscovered in the 1990s8,38 and named translation validation. On each run of compilation, the source and target programs are checked for semantic equivalence, using heuristics that rely on static analysis and hints from the compiler, such as the sequence of transformations applied to the program. In effect, the validation program attempts to discover a stepwise correspondence—a (bi)simulation relation—between the behaviors of the source and target programs. This technique was applied in Necula36 and Zuck et al.49 to certify several optimizing compiler transformations.
In the late 1990s, Rinard proposed40 that each compiler transformation could simply generate a suitable correspondence relation. This relation acts as a certificate of program equivalence, which is valid if it is a (bi)simulation. A single (bi)simulation-checking validator thus suffices to check the correctness of a variety of program transformations. In one such instance,33 certifying the SSA transformation required only 200 lines of additional certificate-generation code (over a 1,000-line SSA transformation), and the implementation was completed in three person-weeks, illustrating the considerable savings in effort that can be achieved through certification.
Program transformations can take unusual forms. The work in Pnueli et al.38 certifies a transformation from a synchronous dataflow language (Signal) to asynchronous sequential code in C. Self-certification is applied in Arons et al.1 to show backward compatibility for microcode, establishing that a new, manually generated microcode has equivalent behavior to the original microcode on the original hardware.
Formalizing Self-Certification
The examples in the previous section illustrate the diversity and scope of self-certification. We now propose a formal definition of a self-certification framework inspired by the formulations in McConnell et al.28 and Wasserman and Blum,47 and discuss desirable properties.
Let X be an input domain, Y an output domain, and let be the set of Booleans. A specification ψ over X,Y is a relation between X and Y or, equivalently, a subset of X × Y . For example, one formulation for the Hamiltonian path problem is to consider X to be the set of finite graphs and Y to be ; the specification consists of pairs (x, y), where y is true if and only if graph x has a Hamiltonian path.
A certification scheme for a specification ψ is a pair (W, ) where W is a domain of witnesses and : X × Y × W→ (read as “valid”) is a validation function. A certificate is a triple (x, y, w) ∈ X × Y × W. A self-certifying program P for ψ has the signature P : X → Y × W.
For every input value, program P generates an output value and a witness. For input x, output y, and witness w, the output is accepted if, and only if, (x, y, w) is true.
Properties of certification schemes. The essential property required of a certification scheme is the soundness of the validator: namely, if the validity test succeeds, the specification must be met. Formally, it must hold that for every x, y, w ∈ X × Y × W, if (x, y, w) is true then (x, y) ∈ ψ. In its equivalent contrapositive form, soundness ensures that incorrect results are never accepted, that is, if the output y is such that (x, y) ∉ ψ, there is no witness w for which (x, y, w) is true.
There are several other desirable, but not essential, properties for a certification scheme. Some can be formulated precisely; others, while important, appear to be difficult to formulate in precise mathematical terms.
Completeness. A scheme is complete if for every (x, y) in ψ, there is a witness w such that (x, y, w) is true. The function that is false everywhere is trivially sound but is certainly not complete. A good certification scheme is one that is as complete as possible.
Computability. One would want the witnesses of a complete scheme to be computable, but this may not always be possible. For instance, a witness for the Halting problem may be the number of steps within which the input Turing machine halts on its initial tape. This form of witness can be checked algorithmically, since the checker simply simulates the Turing machine to determine whether it halts within the specified number of steps. Computing this witness is, however, impossible in general, as it requires solving the Halting problem. But the witness format is still useful for checking the correctness of termination claims determined by a heuristic (but necessarily incomplete) procedure.
Small trusted base. A good validation function should rely on a small trusted base. This notion is intuitively useful, as the smaller the trusted base, the more one can depend on the result of the validation. What is considered trusted, however, may be subjective, as it depends on the user’s familiarity with and knowledge of the specification domain. For instance, we relied on Kuratowski’s theorem to formulate a certificate for graph non-planarity. Those unfamiliar with the theorem may not be convinced of a proof of non-planarity that consists of an embedding of K5 or K3,3 in the input graph.
Furthermore, the implementation of a certificate checker may rely on software not known to be correct. For instance, one tends to trust the results of theorem-proving tools and decision procedures, such as SMT solvers; yet they do have bugs. In fact, it is hard to conceive of a trusted core that is fully trustworthy and can perform all checks. From this viewpoint, it helps that a certificate depends only on the specification; this implies that one may be able to check a claimed certificate in several different ways. For instance, a certificate of program equivalence can be checked with different SMT solvers; if it passes all those tests, one’s confidence in its validity is increased.
Efficiency. It may seem that efficiency should be a required property for a certification scheme. There are two separate concerns: the efficiency of certificate validation and the efficiency of certificate generation. The validation process depends only on the chosen certification scheme. The difficulty of certificate generation varies with the program being certified. Few programs are designed to be self-certifying. It is thus more common to turn a non-certifying algorithm into a certifying one by adding auxiliary data structures and auxiliary computation, which may be expensive. For instance, we saw earlier that to obtain a certificate from bubblesort, it is necessary to store and generate an auxiliary permutation.
Blum’s “simple checker” requires that validation time should be o(T(n)) for a program that has time complexity T(n). That seems unsatisfactory, as the cost of validation is in terms of the cost of a particular algorithm and not in terms of the specification to be met. We prefer to view efficiency relative to the cost of checking the specification: Certification is efficient if it is simpler to generate and validate the certificate than to check whether the output value meets the specification.
Reductions. A certification scheme depends only on the problem specification. This property makes it possible for different solutions to a problem to share a common certificate format and certificate validator. For example, the certificate of bubblesort applies to any sorting algorithm. Another useful consequence is it allows a reduction from one problem specification to another, so one can set up a certification scheme for the first problem in terms of an existing certification scheme for the second.
We saw one such reduction earlier, where a certification scheme for the Hamiltonian Path problem is defined in terms of a certification scheme for Boolean formula validity (that is, unSAT). By the formulation of NP, this is possible in principle for any problem in NP. The advantage is that one needs only to construct provably correct certificate checkers for SAT and unSAT to obtain certification for a large class of important questions. The correctness of each reduction must be proved separately. As reductions operate at the level of specifications, we may expect such proofs to be simpler in nature and easier to mechanize than proofs of the correctness of implementations.
Consider problems A and B with their respective input and output domains and specifications. A reduction r from A to B is a function that maps XA × YA to XB × YB with the following property: For any x in XA and y in YA, if the specification ψB holds for r (x, y), then specification ψA holds for (x, y).
A primary use for a reduction is to derive a certification scheme for A from a scheme for B. Let (WB, VB) be a certification scheme for B. Let WA = WB and VA (x, y, w) = VB (r (x, y), w). This induced scheme is sound for A. (Proof: Consider x, y, w such that VA (x, y, w) holds. By definition, VB (r (x, y), w) holds. By soundness of the scheme for B, it follows that r (x, y) satisfies ψB. By the correctness of the reduction, (x, y) satisfies ψA.)
This discussion on completeness and reduction gives rise to two questions on the universal applicability of self-certification. First, is there a systematic way to formulate a certification scheme for any specification? Second, is there a universal problem such that certification schemes for any other problem can be derived from it through a reduction?
Conclusion
The design of correct programs is a fundamental question in computing, one of great practical and mathematical interest. Self-certification weakens the classical verification requirement to one that holds for each individual program execution, making it feasible (as in the diverse cases illustrated here) to give precise, formal correctness guarantees for implementations of a scale and complexity that place them well out of reach of the traditional verification methods. We hope these illustrative examples encourage readers to consider incorporating self-certification mechanisms into their software systems.
A promising approach to certifying complex systems is to combine certificates generated for individual components of a large software system, using formal assume-guarantee reasoning methodologies to ensure that the composition of the individual certificates is a valid certificate for the behavior of the entire system. For a single component, one would certify its guarantee after checking its assumption. When the assumption is not met, however, the certificate may only be able to point out that this is the case.
Many fundamental questions about certification remain open: Do universal certification mechanisms exist? How could one certify the behavior of non-terminating programs, such as control programs and operating systems? How does one certify machine-learning models for tasks where the specification is itself inherently imprecise or incomplete? We hope this article spurs readers to consider and find practical answers to these questions.
Acknowledgments
Kedar Namjoshi was supported in part by DARPA under contract HR001120C0159 during the preparation of this article. Lenore Zuck was supported by the National Science Foundation under Grant Nos. CCS-2140207 and SHF-1918429, by the Department of Defense under Grant No. W911NF2010310, and by the Discovery Partners Institute of the Universities of Illinois . The views, opinions, and/or findings expressed are those of the author(s) and should not be interpreted as representing the official views or policies of the Department of Defense, the U.S. Government, or the DPI. The authors would like to thank Al Aho, E. Allen Emerson, Kenneth McMillan, Bilha Mendelson, and the anonymous referees for insightful comments on earlier drafts of this manuscript.



Join the Discussion (0)
Become a Member or Sign In to Post a Comment