Dynamic Placement in Refugee Resettlement

1. Introduction

There are 27 million refugees around the world.²² The United Nations High Commissioner for Refugees (UNHCR) considers over 1.4 million to be in need of resettlement, that is, permanent relocation from a temporary country of asylum to a third country.²¹ Resettlement is mainly targeted at the most vulnerable of refugees, such as children at risk, survivors of violence and torture, and those with urgent medical needs. Dozens of countries around the world resettle refugees, but every year the number of refugees in need of resettlement far exceeds the number that is actually resettled. In 2019, for example, only around 63,000 refugees were resettled.²¹

Historically, most hosting countries have paid little attention to which communities inside the country the refugees are resettled. This policy might be worth reconsidering, however, in light of ample evidence that the initial local resettlement destination dramatically affects the outcomes of refugees.^{4–7,9,12,15,19} One variable impacted by community placement is whether and when resettled refugees find employment, which plays a key role in a refugee’s integration by “promoting economic independence, planning for the future, meeting members of the host society, providing opportunity to develop language skills, restoring self-esteem and encouraging self-reliance”.¹

To help more refugees find employment, the U.S. resettlement agency HIAS (founded as the Hebrew Immigrant Aid Society) started in 2018 to match refugees to communities with the software Annie™ Moore (Matching and Outcome Optimization for Refugee Empowerment) developed by Ahani et al.² Based on past arrival data, this software estimates how likely a refugee is to find employment in each community. The software then suggests where to place the refugee to maximize the expected total employment, subject to not exceeding community capacities and ensuring that refugees have access to needed services.

A key limitation of the existing software, however, was that it solved an offline optimization problem whereas refugee allocation is an online problem: whereas Annie™ optimized a one-shot matching of refugees to communities, organizations like HIAS continuously allocate refugees over the year as they are cleared for resettlement, and they aim to maximize the total employment across the year. Due to this mismatch, resettlement practitioners applied Annie™ as a greedy algorithm. That is, Annie™ myopically maximized the employment of the current batch of refugees, without considering whether the current assignment would negatively impact the employment of future arrivals in the same fiscal year by prematurely using up community capacity.

In this paper, we design an online algorithm for refugee allocation. This algorithm achieves higher employment by explicitly accounting for the value that a community’s capacity has for the employment of future arrivals, which we refer to as the community’s potential. In fact, we design two closely related algorithms, defined by different ways of computing potentials from the dual values of a matching linear program. One of these potentials is motivated by stochastic programming and the other by Walrasian equilibrium. Our resettlement model is rich and captures all of the relevant practical features of the refugee resettlement process including indivisible families of refugees, batching, and unknown numbers of refugee arrivals. We evaluate the performance of our algorithms on HIAS data from 2014 until 2019. We show that our algorithms achieve over 98% of the hindsight-optimal employment in all years, whereas the greedy baseline typically achieves only around 90%. We then describe how we implemented our algorithms within an updated version of Annie™.

2. Institutional Background

Resettlement of refugees to the United States is managed by the U.S. Refugee Admissions Program (USRAP), within annual quotas authorized by the president.

Applications for the resettlement program take place from outside of the U.S., typically in refugee camps. The U.S. government conducts security checks, medical screening, and performs cultural orientation, which can take upwards of 18 months.¹⁶ After clearance, USRAP decentralizes the process of welcoming refugees to nine non-governmental organizations known as resettlement agencies, of which one is HIAS. Each agency works with their own network of affiliates supported by local offices, and often religious entities like churches, synagogues, or mosques, which serve as community liaisons for refugees. Each agency works with dozens of affiliates, and the number of affiliates can fluctuate over time. Some affiliates lack services to host certain kinds of refugees. For example, certain affiliates do not have translators for non-English-speaking refugees or lack support for single-parent families.

Agencies have no influence on what refugees are cleared for resettlement by USRAP or on when the refugees might arrive. Resettlement agencies meet on a weekly or fortnightly basis to allocate among themselves the refugees that have been cleared by USRAP. Refugees are usually resettled with members of their families. Such an indivisible group of refugees is referred to as a case. As a family can split when its members are fleeing their home country, some refugees who are applying for resettlement might already have existing relatives or connections in the United States. Such cases with U.S. ties can only be resettled near their existing ties. All other refugees, referred to free cases, can be resettled into any agency’s affiliates, subject to resource availability.

Each affiliate has an assigned annual capacity for the number of refugees (rather than cases), it can admit in a given fiscal year.^a These capacities are approved by USRAP and, in theory, cannot be exceeded by agencies. In practice, capacities can be slightly adjusted toward the end of the year or, as in recent years, substantially revised in the course of the year. Since capacities limit the number of refugees arriving in a fiscal year rather than allocated in it, and since there is typically a delay of multiple months between the two events, the Department of State tells the resettlement agencies an estimated arrival date for each cleared case. Agencies are assessed annually by USRAP on their performance in finding employment for refugees within 90 days of their arrival. Data on 90-day employment is, therefore, diligently collected by the affiliates and monitored by the agencies.

3. Model

An instance of the matching problem first defines a set L of affiliates. Each affiliate ℓ has a capacity c_ℓ ∈ ℕ of how many refugees it can host. On the other side of the matching problem is a set N = {1, …, n} of cases. Each case i represents an indivisible family of s_i ∈ ℕ_≥1 refugees. Furthermore, each case i, for each affiliate ℓ, has an employment score u_i,ℓ, which indicates the expected number of case members that will find employment if the case is allocated to ℓ. Typically, these employment scores u_i,ℓ are real numbers in [0, s_i], but we will also allow to set u_i,ℓ = –∞ to express that case i is not compatible with affiliate ℓ. We will refer to the combination of a case’s size and vector of employment scores as the characteristics of the case. To ensure that the matching problem is always feasible, we will assume that L contains a special affiliate ⊥ that represents leaving a case unmatched, where u_i⊥ = 0 for all cases i and c_⊥ = ∞.^b

We use the employment scores developed by Ahani et al.,² and we give details on data preprocessing and training in the appendix of the full version. Throughout this paper, we evaluate algorithms directly on the employment scores, and we refer the reader to Ahani et al.² for an evaluation of how accurately the employment scores predict employment outcomes.

The goal of the matching problem is to allocate cases to affiliates such that the total employment, that is, the sum of employment scores, is maximized, subject to not exceeding capacities. In the offline problem, where the characteristics of all cases are known a priori, total employment can be maximized by the integer linear program (ILP) below, where variables x_i,ℓ indicate whether the case i ∈ N is matched to affiliate ℓ ∈ L:

The linear programming (LP) relaxation of this ILP is obtained by replacing x_i,ℓ ∈ {0, 1} with x_i,ℓ ∈ [0, 1] for all i ∈ N, ℓ ∈ L. For a fixed matching, we define the match score of case i as its employment score $u_{i,{\ell }_i}$ at the affiliate ℓ_i where it is allocated; we will also refer to its match score per refugee, $u_{i,{\ell }_i}/s_i$.

Finally, cases arrive online and in batches. That is, in time step t = 1, 2, …, the characteristics of cases {i_t−1 + 1, i_t−1 +2,…, i_t} get revealed (where i_t > i_t−1 and i₀ = 0), and these cases must be assigned immediately and irrevocably. The online matching algorithm must still produce a matching whose indicator variables x_i,ℓ satisfy the constraints of the ILP above, but—since each batch must be allocated before the characteristics of subsequent batches are known—its objective value will typically fall short of the optimal matching in hindsight. While we will not commit to a specific model of how the characteristics of arriving cases are generated, these arrivals should be thought of as stochastic rather than worst-case, and the distribution of case characteristics as changing slowly enough that sampling from recent arrivals is a reasonable proxy for the distribution of future arrivals.

4. Algorithmic Approach

To motivate our algorithmic approach, we begin by describing why the matching systems previously deployed in practice lead to suboptimal employment. These systems assign cases greedily. That is, if we assume for simplicity that cases arrive one by one, they match an arriving case i to the affiliate ℓ with the highest employment score u_i,ℓ among those that have at least s_i remaining capacity. The main problem with greedy assignment is that it exhausts the capacity of the most desirable affiliates too early. Specifically, we observe in the data that a large fraction of cases has their highest employment score at the same affiliate ℓ* but that the size of the employment advantage of affiliate ℓ* over the second-best affiliate varies. Since greedy assignment only considers the highest-employment affiliate for each case, it will fill the entire capacity of ℓ* early in the year, including with some cases that benefit little from this assignment. Consequently, cases that would particularly profit from being placed in ℓ* but arrive later in the year no longer fit within the capacity.

Conceptually, the decision to match a case i to an affiliate ℓ has two effects: the immediate increase of the total employment by u_i,ℓ but also an opportunity cost for consuming ℓ’s capacity, which might prevent profitable assignments for later arrivals. Since greedy assignment only considers the former effect, it leaves employment on the table.

Our algorithm PMB (“potential match with batching”) takes into account both the immediate employment benefit and the opportunity cost of consuming capacity. Whenever a batch of refugees arrives, PMB first computes a potential p_ℓ ≥ 0 for each affiliate ℓ. These potentials stand in for the per-unit opportunity cost of using ℓ’s capacity, and their calculation is described later. Once the potentials are computed, PMB allocates the current batch based on an ILP. However, the ILP’s objective is not simply maximizing total employment ${\sum }_i{u}_{i,{\ell }_i}$ as in greedy assignment (where i ranges over the cases in the batch, and ℓ_i is the affiliate to which i is assigned). Instead, the ILP’s objective ${\sum }_i{u}_{i,\ell }-s_i{p}_{{\ell }_i}$ deducts the potential of consumed capacity from total employment. Pseudocode for this algorithm can be found in the full version of this paper.

We now describe the remaining piece of the algorithm, namely, how to compute the potentials. Suppose for now that the remaining arrivals of the fiscal year were already known. Then, we can write an ILP to allocate the current and future arrivals such that total employment is maximized, subject to the remaining capacity. If we consider the LP relaxation of this ILP, the optimal dual value of affiliate ℓ’s capacity constraint measures how much the optimal employment would increase for a one-unit increase in ℓ’s capacity—that is, this dual variable is closely related to the opportunity cost we want to measure. Even though we do not actually know the future arrivals, we can use this insight to compute potentials by simulating plausible sequences of future arrivals: k times, we simulate such a sequence by sampling with replacement from the past six months of arrivals, compute the dual variables for each sequence as above, and set ℓ’s potential p_ℓ to the value of ℓ’s dual variable, averaged across the k sequences.

In fact, we evaluate two different potentials, which fill in the details of the sketch above in two different ways, each motivated by connections to different areas of the literature. The first potential, Pot1, does not include the current batch in the matching LP and breaks ties among optimal dual solutions in favor of the element-wise maximal solution. As we explain in the full version, this definition has close connections to two-stage stochastic programming. By contrast, Pot2 includes the current batch in the matching LP and selects the element-wise minimal set of dual values. In the appendix of the full version, we describe that this definition is motivated by a connection to Walrasian equilibria in matching. These two potentials define two distinct versions of our algorithm PMB, PBM(Pot1) and PBM(Pot2), both of which we evaluate in the next section.

5. Empirical Evaluation

In this section, we evaluate the employment outcomes of the PMB algorithms on yearly arrival data at HIAS, for six fiscal years, from 2014 to 2019. As affiliates closed and opened across these years, the number of affiliates varies between 16 and 24 (not counting the unmatched affiliate ⊥). Finally, the number of arriving refugees (respectively, cases) varies between 1670 (resp., 640) and 4150 (resp., 1630) across fiscal years.

Our evaluation is split into three parts, with successively richer models of refugee assignment: In Section 5.1, we consider the classical online bipartite matching setting, which means that all cases consist of single agents, that they arrive one by one rather than in batches, and that the total number of arriving refugees is known to the algorithm. Then, in Section 5.2, we abandon the first two assumptions. We show that the performance of our algorithms is hardly impacted by the fact that cases consist of multiple refugees and arrive in batches. Finally, in Section 5.3, we show that accurate estimates of the total number of arrivals are crucial for the algorithms’ performance, and we draw lessons from this for practical implementation.

5.1. Online bipartite matching

We begin our analysis in a simplified setting of refugee resettlement, which is exactly online bipartite weighted matching. Specifically, this means that all cases consist of a single refugee and that refugees arrive one by one rather than in batches. To make the arrival data satisfy the first condition, for this subsection only we split each case of size s_i > 1 into s_i identical single-refugee cases with a 1/s_i fraction of the original employment scores. We begin our analysis in this simplified setting because it is where the theoretical arguments underlying our potentials apply. In particular, the LP relaxation of the matching ILP (about which we gain information through the dual values) faithfully represents the matching ILP. In Section 5.2, we will abandon these simplifying assumptions and observe that our general observations continue to hold for larger cases and batching.

For the capacities, we use the year’s final, that is, most revised, capacities.^c We also immediately take into account that affiliates are restricted in which nationalities, languages, and family sizes they can accommodate, as well as in whether they can host single-parent families.

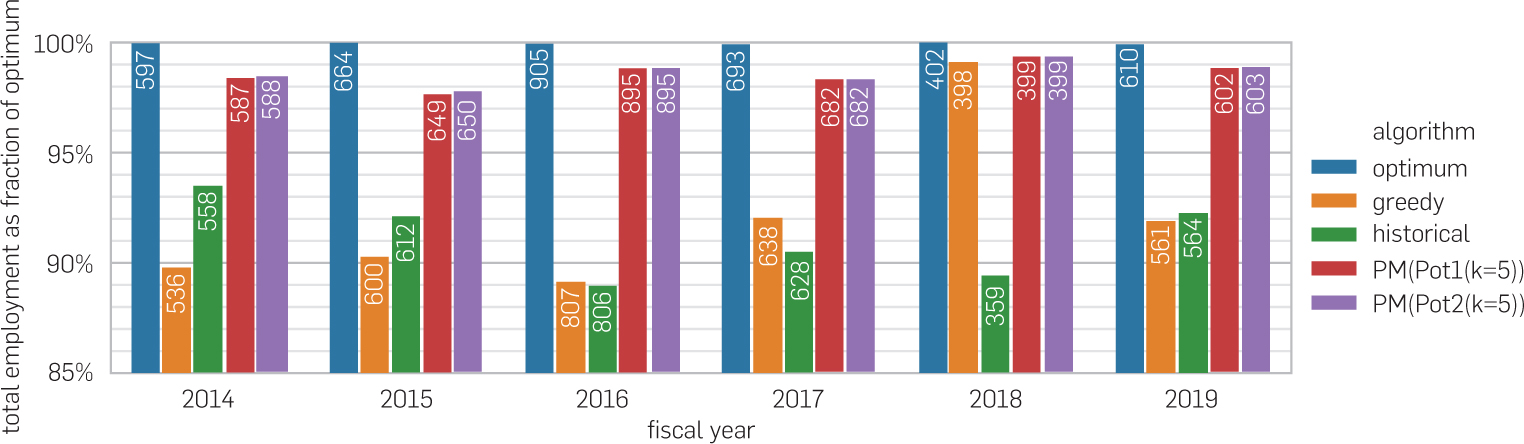
As shown in Figure 1, even the greedy baseline obtains a total employment between 89% and 92% of the optimum matching in hindsight. (The year 2018 is an outlier, which we discuss next.) Nevertheless, the greedy algorithm leads to between 50 and 100 fewer refugees finding employment every year compared to what would have been possible in the optimum matching. Our potential algorithms close a large fraction of this gap, obtaining between 98% and 99% of the optimal total employment. This holds both for algorithms based on Pot1 and for those based on Pot2 (which we will compare in detail in Section 5.2).

The fiscal year 2018 stands out from the others due to the fact that the greedy algorithm performs on par with our potential algorithms, at 99% of the hindsight-optimal total employment. This is easily explained by the fact that the capacities are much looser than in other fiscal years: whereas, in all other fiscal years between 2014 and 2019, the number of arriving refugees amounts to between 84% (2019) and 97% (2016) of the final total capacity across all affiliates, this proportion is only 48% in 2018. Since capacity is so abundant, the optimal matching will match a large fraction of cases to their maximum-score affiliate, and the greedy matching is close to optimal.

We also compare the employment obtained by the allocation chosen by HIAS (“historical”). This comparison gives the historical matching a slight advantage, as HIAS sometimes overrides the incompatibility between an affiliate and a case, which we do not allow any other algorithm to do.^d

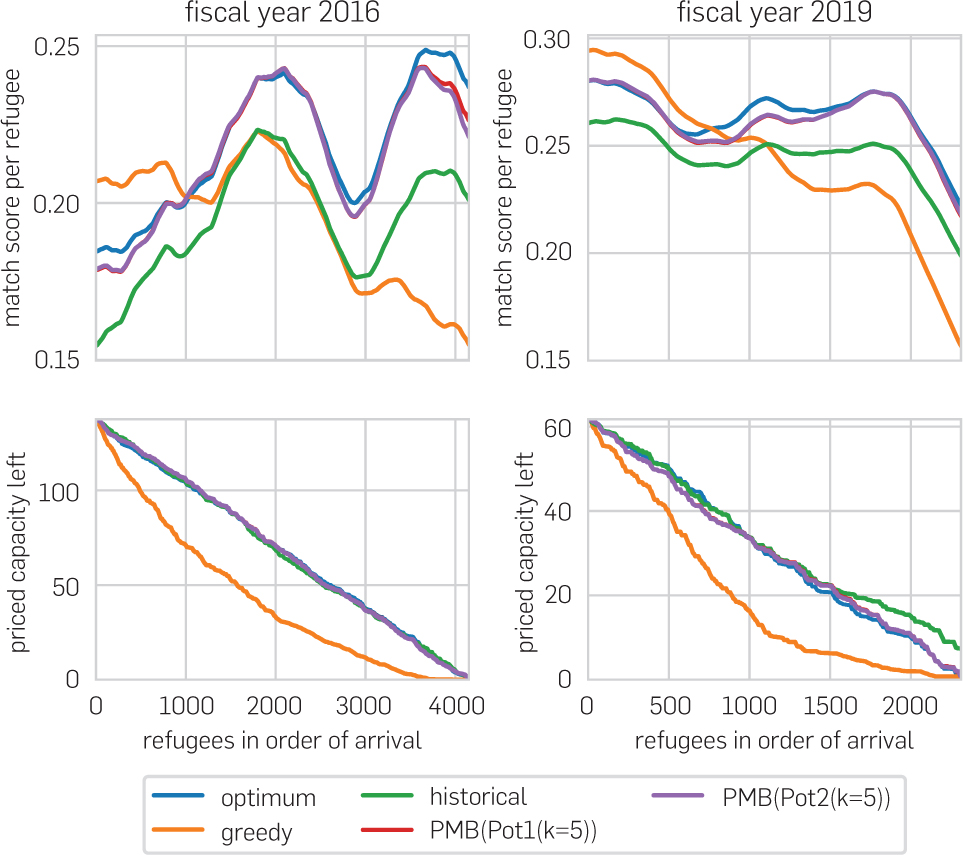
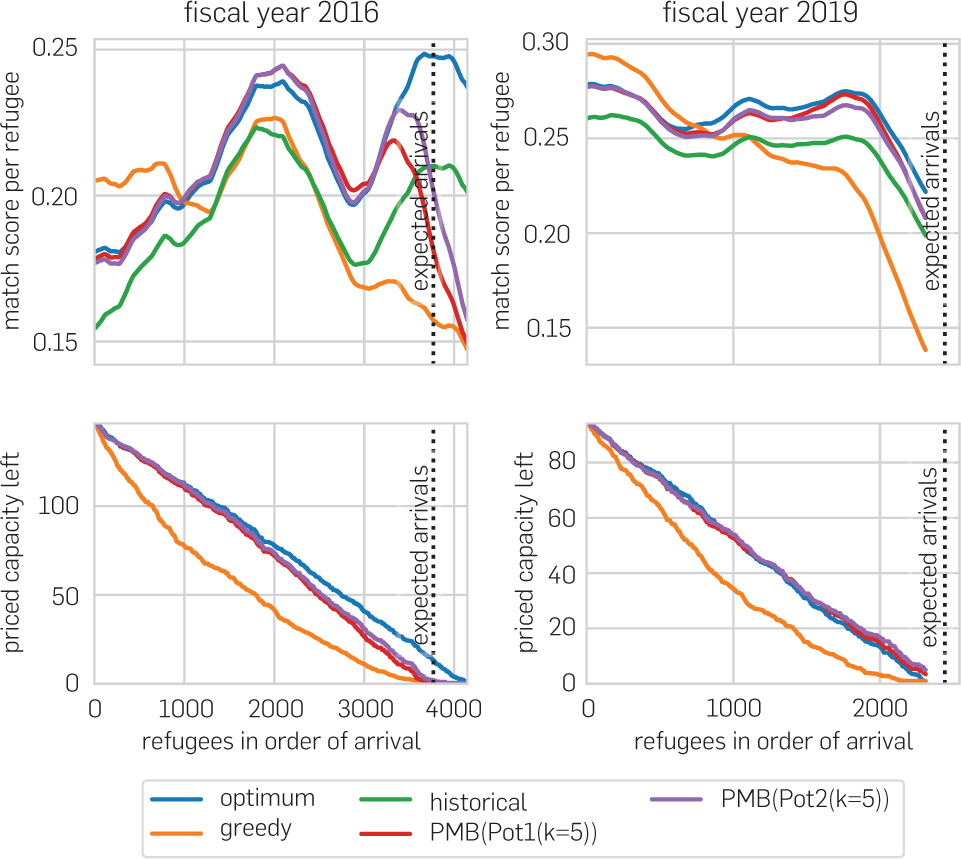
In the top half of Figure 2, we investigate how the match score changes over the course of two fiscal years, 2016 and 2019, chosen to contain a year in which the greedy and historical base-lines perform relatively poorly and one in which they perform well. These two graphs allow us to draw several conclusions:

• Our algorithms track the optimum very close throughout the course of the year.

• The historical match scores produced by HIAS track the optimum match score trajectory but are consistently below it.

• The greedy algorithm produces higher match scores than the optimum early in the year. However, because the greedy algorithm uses priced capacity too quickly, it produces a very poor match score toward the end of the year (especially in 2016).

We also illustrate these three features in the bottom half of Figure 2, where we visualize the amount of capacity remaining in the most valuable affiliates. Specifically, considering all arrivals of the fiscal year, we compute the dual values of the affiliates’ capacity constraints in the matching LP. At any point in time, we can then weigh the remaining capacity by these prices to obtain a priced capacity. The bottom half of Figure 2 shows the following:

• The optimum-hindsight matching and the potential algorithms use up the priced capacity at a roughly constant pace and essentially consume it all.

• HIAS consumed priced capacity close to a near-constant pace very similar to that of the optimum.

• The greedy algorithm uses up the capacity very quickly, such that at the median refugee, only 22% (2016) or 17% (2019) of the priced capacity is left.

In other words, while HIAS used capacities reasonably well over the course of the reference years, it has fallen short of finding efficient matchings. As we show in Section 5.3, the ability of HIAS resettlement officers and of our algorithms to use capacity well over the course of the year depends crucially on being able to predict arrival numbers.

5.2. Non-unit cases and batching

We now return to the realistic setting in which cases can consist of multiple family members, and in which cases arrive in batches. This means that considering the LP relaxation is now a proper relaxation of the matching ILP, and that we allocate multiple refugees at once without recalculating the potentials within the same batch. Since the capacities of most affiliates are relatively large, however, we would expect both approximations to be relatively close. Indeed, we find empirically that the employment numbers remain essentially unchanged from Figure 1 (see the full version).

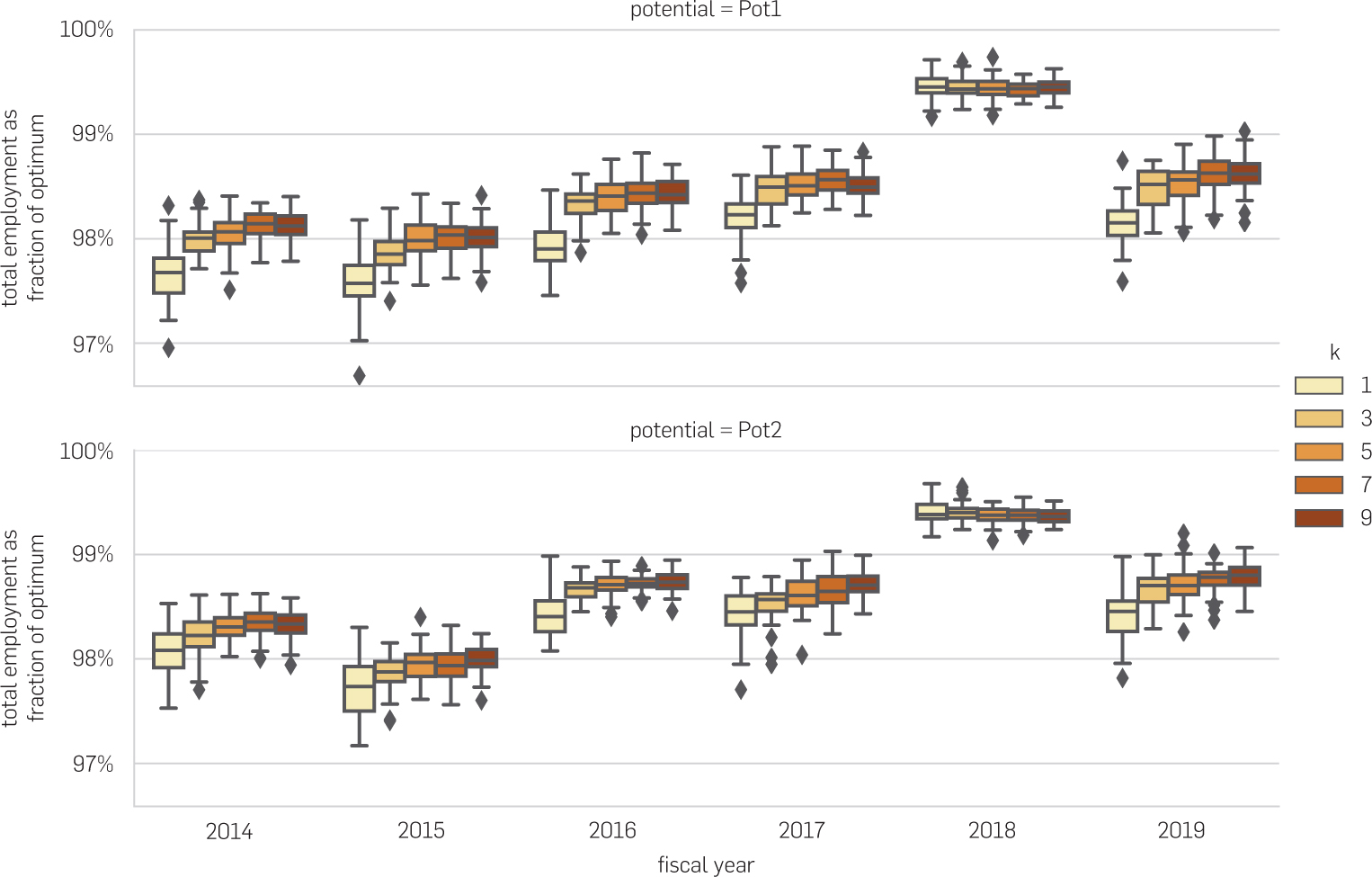
Since processing entire cases in batches are much faster than processing cases (or individual refugees) one by one, we are now in a position to run each potential algorithm many times and analyze the distribution of total employment. As shown in Figure 3, the total employment produced by each potential algorithm is sharply concentrated, especially for k ≥ 3 trajectories to compute duals.

Running each algorithm many times enables us to compare the relative performance of the potential algorithms. Across both ways of computing potentials, and all fiscal years (with the exception of 2018, where differences are challenging to discern), we see a clear tendency that averaging the potentials across more trajectories improves the employment outcome. These effects are somewhat limited, though, as going from a single trajectory to nine trajectories improves the median employment by less than half a percent of the hindsight optimum. As is to be expected, there appear to be diminishing returns in increasing k.

For k held constant, we observe that the Pot2 variants quite consistently outperform the Pot1 variants; again with the exception of 2018, in which a small inversion of this trend can be seen. While all potential algorithms perform very well, based on these results, we recommend the Pot2 potentials with a relatively large k for practical implementation. Of course, increasing k increases the running time of the matching algorithm. However, since a resettlement agency computes only one set of potentials per day, the algorithm runs in a few seconds even for k = 9.

5.3. Unknown arrival number

Unlike the greedy algorithm, our potential algorithms require as part of their input an estimate of the total number of arriving refugees or cases. In principle, resettlement agencies should receive this information from the Department of State. In fact, HIAS and the State Department set affiliate capacities such that the sum of all capacities equals 110% of the number of refugees that HIAS will host in the fiscal year.^e

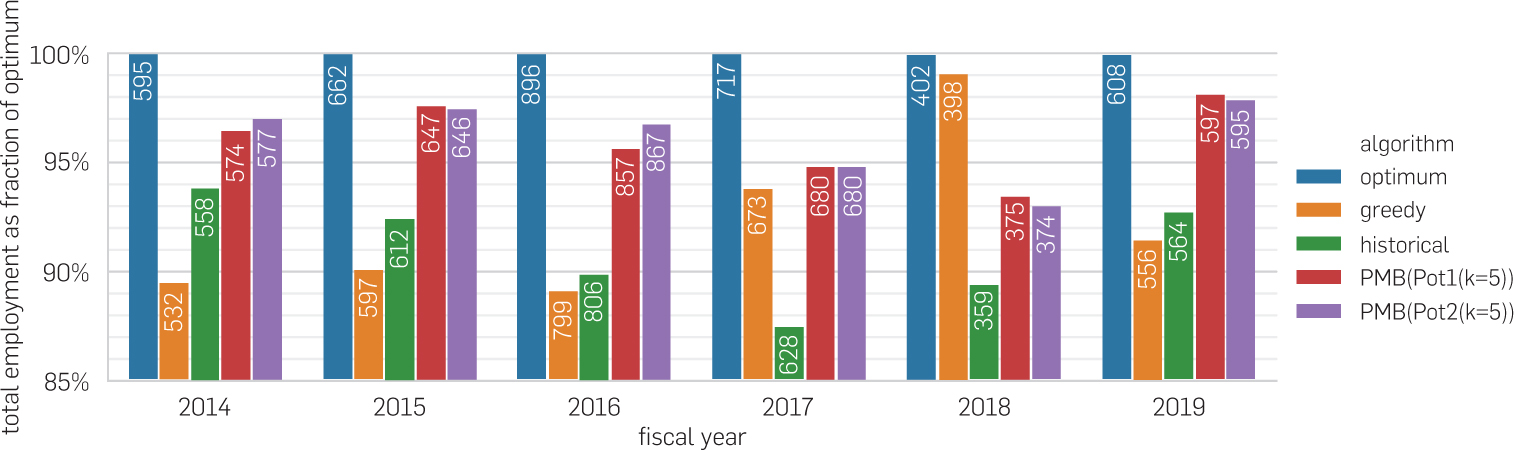
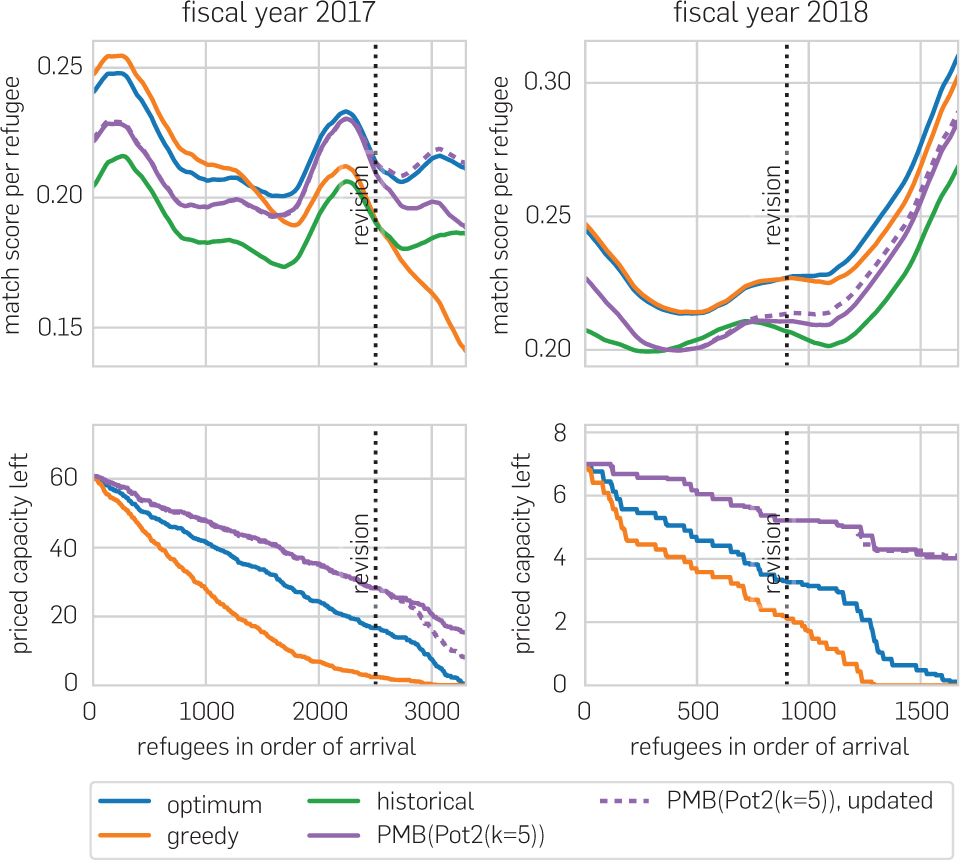
It is therefore natural to run our potential algorithms under the assumption that the number of arriving refugees will be 1/(110%) ≈ 91% of the total announced capacity. The result of this strategy is shown in Figure 4. As we choose the initial, unrevised capacities, the employment scores of the hindsight optimum and the greedy algorithm may differ from those in previous experiments, which used the most revised capacities.^f In all fiscal years other than 2017 and 2018, the imprecise knowledge of future arrivals deteriorates the approximation ratio of the potential algorithms, but the potential algorithms continue to outperform the greedy baseline, and they outperform the historical even in these years.

Putting aside the years 2017 and 2018 for now, we investigate the fiscal years 2016 and 2019, in which arrivals were highest and lowest relative to the announced capacity. In the fiscal year 2016, the total arrivals were particularly large relative to the initial capacity: the arrival numbers added up to 100% of the initial capacity rather than 91%, which means that our potential algorithms expected around 3770 refugees to arrive rather than the 4150 that ended up arriving. As a result, the potential algorithms consume the priced capacity at an approximately constant rate, consuming it all around the expected number of expected refugees (Figure 5, bottom left). Up to this point, the potential algorithms are more generous in consuming capacity than would be ideal given the actual number of arriving cases, which is why the potential algorithms obtain slightly higher average employment over the first three-quarters of arrivals (Figure 5, top left) than the optimal matching in hindsight. For refugees arriving after the 3770 expected refugees, however, the capacity in the best affiliates is used up, which is why the averaged employment sharply drops after this point.

In 2019, by contrast, fewer refugees arrived than expected, only 86% of the total capacity. At the bottom right of Figure 5, it is visible that the potential algorithms consume priced capacity at a slightly lower rate than the optimal algorithm in hindsight, as they aim to use up the capacity of around 2440 refugees rather than the 2310 who ended up arriving. This effect is reflected in the average employment rates (top right), which lie below that of the optimal algorithm throughout most of the year.

The fiscal years 2017 and 2018 stand out due to the fact that the total number of arriving refugees fell far short of the announced number reflected in the approved capacities: in 2017, arrivals amounted to 65% of the approved capacities, while they amounted to only 46% in 2018. Both of these years fall into the beginning of the Trump administration, which not only sharply reduced the announced intake of resettled refugees, but also furthermore abruptly halted the intake of refugees from six predominantly Muslim countries starting in early 2017.

Since the potential algorithm depicted in Figure 6 severely overestimates how many cases will arrive, it holds back much more priced capacity than would be optimal (bottom, solid lines). This causes the potential algorithms to extract less employment throughout the year than the optimal algorithm (top, solid lines). As observed in Section 5.1, the capacities in 2018 are so loose that the greedy algorithm’s pace of consuming priced capacity is not far from optimal.

In both 2017 and 2018, the Department of State eventually corrected the expected arrivals downward and instructing the resettlement agencies to reduce their capacities. As the dashed lines in Figure 6 show, the potential algorithm can make use of these updated arrival number estimates by burning through capacity more aggressively after the revision. In 2017, this update substantially increases the total employment achieved by the potential algorithms (from 95% of the hindsight optimum to 97%), but it has only a minor effect in 2018, where the revision continues to far overestimate the number of arrivals.

Fortunately, a matching algorithm need not solely rely on the official arrival numbers since resettlement agencies such as HIAS already possess much richer information and insights into the dynamics of refugee arrivals. In the fiscal year 2017, for example, HIAS foresaw a worsening climate for refugee resettlement immediately after the November 2016 election and was aware of concrete plans to drastically reduce refugee intake in January 2017, both before these changes were reflected in arrival numbers and before the capacities were officially updated in March 2017. Similarly, HIAS continuously monitors domestic politics and international crises for their potential impact on resettlement, and moreover, it has some limited insight into the resettlement pipeline, which allows it to prepare for changes in arrivals. We, therefore, believe that, rather than attempting to build a sophisticated tool for predicting arrivals in a fully autonomous manner, it is preferable to allow HIAS staff to override our prediction with more advanced information.

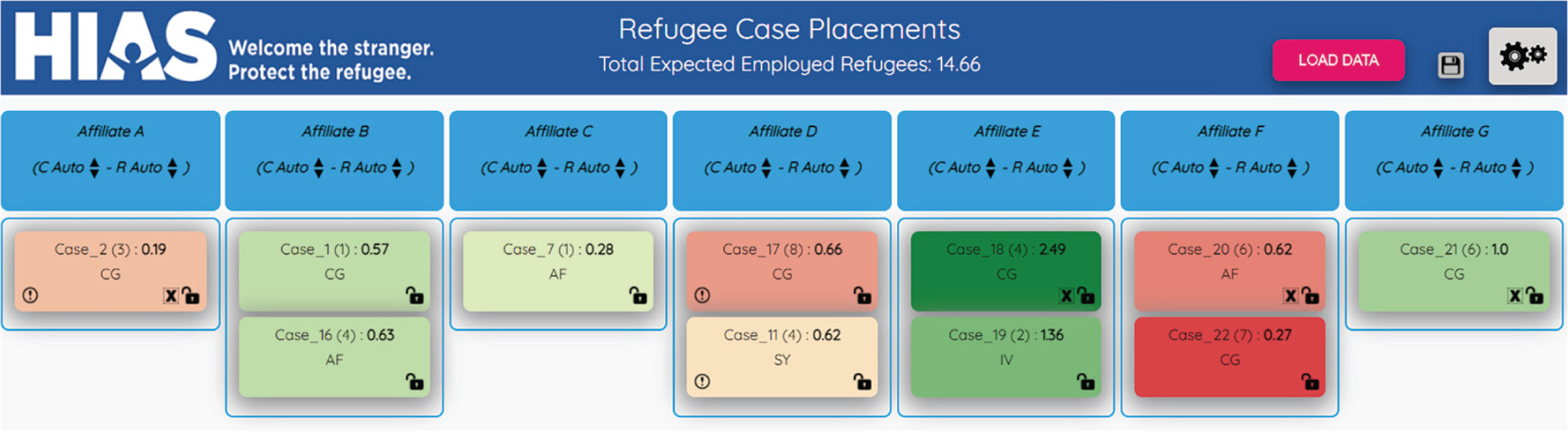
6. Implementation in Annie™

To enable HIAS to benefit from dynamic allocation via potentials, we have integrated new features into its matching software Annie™ Moore. A crucial design requirement is that HIAS staff must be able to override the allocation recommendations of Annie™ when they are aware of requirements outside of our model. As we illustrate in Figure 7, the new interface of Annie™ presents information about affiliate potentials, thereby taking future arrivals into account. Specifically, the background color of the tile for case i encodes the adjusted employment score (green = high, red = low), that is, the original employment score u_i,ℓ less the value s_i p_ℓ of the total capacity consumed in affiliate ℓ. The fact that the algorithm PMB always maximizes the sum of adjusted employment scores in its allocation of the current batch means that the algorithm is explainable in terms of the information presented to the user.

7. Conclusion

We have developed and implemented algorithms for dynamically allocating refugees in a way that promotes refugees’ prospects of finding employment. These algorithms are grounded in theory and perform very well when tested on real data.

While we have tested the algorithms as an autonomous system, the success of Annie™ in increasing employment outcomes in practice will depend on how it performs in interaction with HIAS resettlement staff. In Section 5.3, we already saw that the allocation decisions of Annie™ can greatly profit from human users providing better estimates of future arrivals. Human input is equally crucial in dealing with uncertainty in several other places: for example, HIAS staff might intervene by correcting the arrival year of a case if the Department of State’s estimate seems off, or they might increase some affiliates’ capacities late in the year if they anticipate that these capacities can be increased. By allowing all parameters of the matching problem to be changed, Annie™ allows HIAS resettlement staff to improve the matching using all available information.

Ideally, the human-in-the-loop system consisting of the matching algorithm and HIAS staff can combine the strengths of both of its parts: On the one hand, the algorithms in Annie™ capitalize on subtle patterns in employment data and manage capacity more effectively over the course of the fiscal year. On the other hand, the expert knowledge of HIAS staff enables the system to handle the uncertainty that is inherent in a matching problem involving the actions of multiple government agencies, dozens of affiliates, and thousands of refugees. In light of the U.S. administration’s increase of the refugee intake ceiling from 18,000 in 2020 to 125,000 in 2022, we foresee both parts playing a crucial role: the increasing scale of the problem will make data-based algorithms more effective, and human guidance will be necessary to navigate the evolving environment of a rapidly growing operation.

Acknowledgments

We are deeply grateful to HIAS for providing data and for sharing insights into the practical challenges of refugee resettlement. We thank Siddhartha Banerjee, Avrim Blum, Bailey Flanigan, Daniel Freund, and David Wajc for helpful discussions. This work was supported by Economic and Social Research Council grant ES/R007470/1; by National Science Foundation grants CCF-1733556, CCF-2007080, CMMI-1825348, and IIS-2024287; and by Office of Naval Research grant N00014-20-1-2488.