Differentiable Economics: Strategic Behavior, Mechanisms, and Machine Learning

Economists have developed different types of models describing the interaction of agents in markets. Early models in general equilibrium theory describe agents taking prices as given and do not consider the incentives of agents to manipulate prices strategically. With appropriate convexity assumptions on the preferences, such models can be cast as convex optimization problems for which efficient algorithms are known to find a competitive equilibrium. Price-taking behavior might be a reasonable approximation of agent behavior in large markets, but it does not adequately capture the incentives and strategies that agents have in smaller markets or in other strategic settings. Modern models in economics, such as those used for modeling auctions, oligopoly competition, or contests, are based on game theory, with the Nash equilibrium as the central solution concept. Such models derive market outcomes based on the preferences and constraints of individual agents.

Game-theoretic models assume either complete information about the preferences of others or distributional knowledge (also known as a Bayesian game). Several algorithms have been developed to solve the Nash equilibrium problem in finite, normal-form games. For example, the Lemke–Howson algorithm is the best-known algorithm for the two-player, general-sum case. However, finding an equilibrium even in finite, complete-information games has been shown to be computationally hard in general,^10,16 at least in the worst case. Algorithms for larger games with more players or for auctions and other Bayesian games with continuous types and actions are not readily available. The first question that we ask in this article is: Can learning algorithms with self-play find equilibrium in economic models?

Learning algorithms have had some success for certain types of finite, complete-information games.²² No-regret algorithms such as online gradient descent converge to a Nash equilibrium in dominance-solvable, constant-sum, and general-sum 2 x 2 games.²⁷ However, Milionis et al.³¹ showed that there exist games for which such gradient dynamics fail to converge to Nash equilibria for any initialization. Learning algorithms in general games can cycle, diverge, or be chaotic and their dynamics can be complex and difficult to characterize.⁴⁰

Yet many economically motivated games appear to have a structure that can be learned. For example, convergence to equilibrium was shown experimentally in various games of competition, such as models of auctions, contests, or oligopoly pricing. These models have continuous actions (for example, bids) and the competitors are modeled as draws from a continuous distribution. This allows for very general game models, but some of the corresponding equilibrium problems are hard in the class PP (beyond the polynomial hierarchy).¹⁰ These worst-case results on combinatorial auction instances leave open the possibility of empirically useful algorithms for many strategic problems, as they have been analyzed in microeconomics and the management sciences for decades. Until recently, numerical techniques were available only for specific problems.⁷ Neural networks and self-play have provided effective equilibrium learning methods to approximate equilibrium with high precision for a wide variety of central economic models of competition.^3,4 While the learned Bayes-Nash equilibria can always be verified ex-post, characterizing the precise characteristics that determine ex-ante which games can be learned is a much more difficult question. Such games are different from random games or the degenerate games discussed in Milionis et al.³¹ For example, auctions have a monotonic allocation rule that gives them more structure. Yet proving convergence is challenging, and it could only be achieved for selected games so far.¹

The success of machine learning extends beyond static games. New reinforcement learning methods find equilibria in dynamic games with multiple stages.³⁷ Equilibria can be found for game-theoretic settings that were previously considered intractable and where no numerical techniques were available. The result of this more recent line of research is twofold:

• It allows for equilibrium solvers, able to find equilibrium in a wide variety of environments and settings of strategic interaction.

• It allows us to characterize economic environments where learning agents converge to an equilibrium and others where this cannot be expected or where the selected equilibrium does not maximize welfare or revenue. This is particularly relevant when regulators want to understand the efficiency of automated markets with learning agents, as found, for example, in display ad auctions or with pricing agents on retail platforms.

Overall, this work situates the equilibrium problem as a first opportunity of differentiable economics. In a game-theoretic equilibrium problem, differentiable economics refers to the representation of the utility functions of agents in the game in a way that allows for learning algorithms that follow utility gradients. The resulting equilibrium solvers optimize their behavior directly with respect to the desired outcome. The approach to equilibrium computation is different from combinatorial algorithms, such as the Lemke-Howson algorithm. More generally, the term differentiable economics references a solution paradigm that leverages a differentiable representation of a problem, similar to differentiable programming,⁶ a programming paradigm where computer programs are designed to be differentiable, enabling the use of calculus-based optimization techniques such as gradient descent.

Differential economics is related to but different from the recent progress in building agents that achieve super-human performance in combinatorial games such as chess and Go.⁴¹ First, economic games such as auctions, oligopoly competition, or contests typically have a continuous action space expressed in money, and opponents are modeled as draws from a prior distribution that has continuous support. Second, differentiable economics is focused on modeling and achieving equilibrium behavior (which may or may not be super-human).

The second opportunity in differentiable economics is to use data-driven methods and machine learning to discover rules, constraints, and affordances—mechanisms—for economic environments that promote good outcomes in the equilibrium behavior of a system. Mechanism design solves the inverse problem of game theory, finding rules of strategic interaction such that agents in equilibrium will effect an outcome with desired properties. Where possible, mechanisms promote strong equilibrium solution concepts such as dominant strategy equilibria, making it strategically easy for agents to participate. Think of a series of bilateral negotiations between buyers and a seller that is replaced by an efficient auction mechanism with simple dominant strategies for agents to report their preferences truthfully. There is also work on designing mechanisms where the equilibrium play can be learned by a particular learning dynamic.^30,36

Mechanism design problems have proved very hard to solve analytically; for example, there is no known closed-form solution for the design of a revenue-maximizing auction for selling two items to two bidders, even though Myerson³³ solved the single-item problem many decades ago. Computational complexity is also known to be a barrier, at least in some kinds of problem instances; for example, Daskalakis et al.¹⁵ proved it is #P-hard to find the optimal auction in an environment with a discrete product distribution over valuations for multiple items. This raises the question: Can machine learning algorithms find mechanisms with good strategic and economic properties?

Indeed, machine learning has recently led to new progress in mechanism design. Dütting et al.¹⁸ provide the first general-purpose approach for designing approximately revenue-optimizing, approximately incentive-compatible, multi-item auctions using multi-layer neural networks and differentiable economics. They train the networks using samples from value distributions to maximize expected revenue subject to penalizing the failure of incentive compatibility. More recent work has introduced the first general-purpose approach for designing approximately revenue-optimizing, exactly incentive-compatible, multi-item auctions using multi-layer neural networks and post-processing through integer programming.⁴⁴ The approach follows earlier attempts to automate mechanism design,¹² but leverages the power of universal function approximators, such as neural networks, and first-order methods to train these networks. The differentiable economics approach to mechanism design is to represent the rules in a differentiable way such that they can be learned via neural networks.

In what follows, we give an overview of this recent progress in the use of machine learning algorithms to compute equilibria and for the design of optimal mechanisms; we position machine learning as a new tool for theoretical and applied economists who are interested in analyzing, designing, and understanding specific markets and institutions.

Learning Equilibria in Single- and Multi-Stage Games

Here, we focus on auctions as particularly illustrative models in economic theory and central models of competition. Despite the enormous academic attention that this branch of game theory has received, closed-form equilibrium strategies are known only for very restricted, simple market models, such as single-item auctions with independent value distributions. Analytical derivations of equilibrium strategies require strong assumptions and are usually the result of months or even years of work. For multi-item auctions, or for auctions where bidders have non-uniform or correlated valuation distributions or complex utility functions, closed-form equilibrium bid functions are typically not known.

In these market models, the equilibrium problem can be described as a system of non-linear differential equations for which there is no general exact solution theory. Beyond the challenge of finding analytical solutions, numerical techniques for differential equations have turned out to be challenging, and have received only limited attention in economics. Fibich and Gavish²⁰ criticize the inherent numerical instability of standard numerical techniques for solving the differential equations governing certain equilibrium problems.

As introduced earlier, equilibrium learning provides an alternative approach,^25,32,38 but until recently the literature has mostly been focused on finite, complete-information games.²¹ Only recently, new forms of neural equilibrium learning were introduced for auction games.³ These algorithms are based on neural networks and self-play and find equilibrium in a wide variety of sealed-bid auctions. As auction allocations are inherently discrete, the ex-post utilities in auction games have discontinuities and, as a result, are not differentiable. This representation is not differentiable and standard backpropagation would lead to problems. However, one can use evolutionary strategies or other smoothing techniques to compute pseudo-gradients of the ex-post utility function—a differentiable representation. The pseudocode shown in Algorithm 1 provides an overview of how pseudo-gradients can be used to learn in neural networks in spite of discontinuities in the utility function. These pseudo-gradients can be derived as fitness-weighted perturbation noise from evolutionary strategies (ES), and replace traditional backpropagation as a learning algorithm to update weights in neural policy networks.

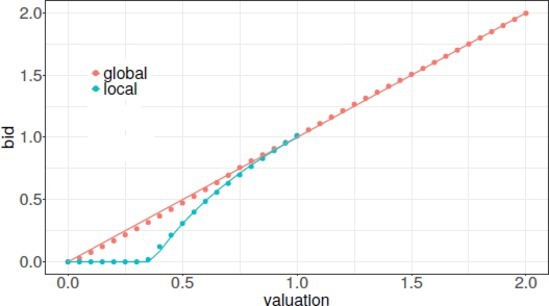
Without such smoothing techniques, the neural networks would only learn to bid zero, which is clearly not an equilibrium. With this, an approximate equilibrium can be learned with high precision in single-item, multi-item, and combinatorial auctions, and for different types of value distributions and utility functions. These learning algorithms can be executed effectively using GPUs. Figure 1 shows the analytical (solid line) and the learned (dotted line) equilibrium strategies for a simple combinatorial auction with a second-price payment rule in a model with two identical items and two “local bidders,” who each want to win one item, and a “global bidder,” who wants to win both items. The global bidder has a dominant strategy to bid truthfully, but the equilibrium bidding strategy of the local bidders depends on the distribution of values, uniform in this example.

Equilibrium play in various asymmetric environments, where the bidders’ values are drawn from different distributions, can also be successfully learned.⁴ Such models have proven to be very challenging analytically, and typically there is no closed-form equilibrium prediction. Ex-post verification allows checking whether a strategy profile learned by an algorithm is an equilibrium or not. The variety of auctions for which equilibria can be successfully learned through these neural equilibrium solvers is remarkable, and includes models with interdependent valuations, complex utilities, and multiple Bayes-Nash equilibria.⁴ In the past, there were no algorithms to compute an equilibrium in such a wide variety of models.

In practice, many important strategic problems have multiple stages. Sequential sales of multiple items via first- or second-price auctions describe a textbook example of such multi-stage mechanisms. Also, requests for quotes in procurement are typically followed by auction, and many contests have multiple stages (where contestants are eliminated, one by one). In dynamic oligopoly games, firms might drop out after making a loss, which changes the competition over time. Recently, Myerson and Reny³⁴ introduced multi-stage games with continuous sets of signals (for example, the valuations of a bidder) and actions. Multi-stage games are flexible in modeling different economic environments and include Bayesian games, stochastic games with finite horizons, and combinations thereof. However, it has been an open question as to how to find equilibria in such games. The sequential sales of multiple items to risk-neutral, unit-demand, and payoff-maximizing bidders can be seen as an exception.²⁸

Deep reinforcement learning (DRL) algorithms such as REINFORCE or proximal policy optimization (PPO) were recently shown to find equilibria in such multi-stage games.³⁷ These policy gradient methods learn randomized strategies in multi-stage games. Modeling randomized rather than pure strategy functions provides another way to deal with the discontinuities in the ex-post utility functions that led to challenges in earlier approaches.³ Rather than custom training algorithms based on evolution strategies, one can use standard backpropagation to train the resulting neural networks. Deep, multi-agent reinforcement learning (MARL) is also being used to study economic and social systems, with MARL modeling agent behavior.^29,46

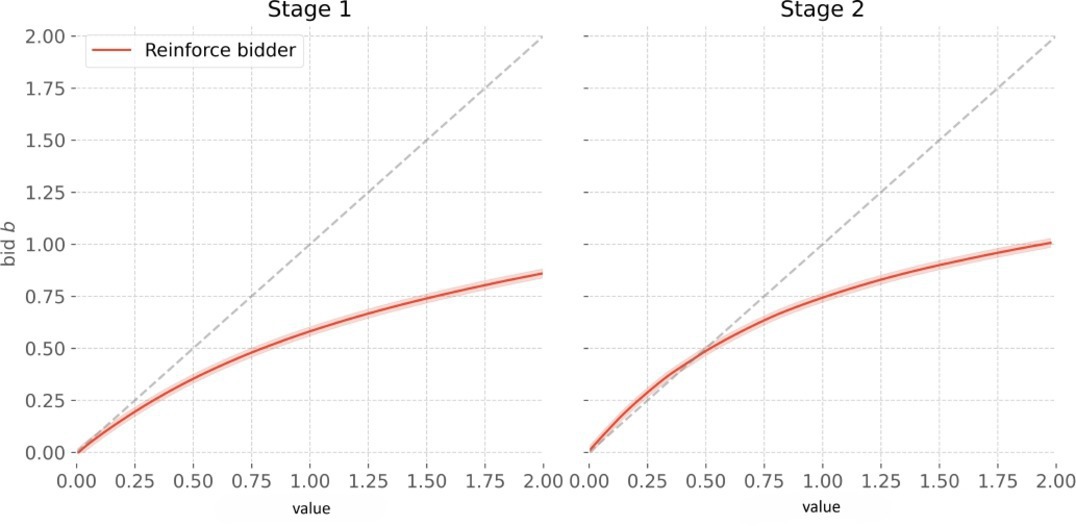
Figure 2 illustrates the equilibrium learned for a sequential second-price auction with two items and three risk-averse (rather than risk-neutral) unit-demand bidders with a common value for the items. Analytical equilibrium strategies are not known even for such a simple sequential auction environment. In contrast to the use of machine learning to solve single-stage auctions, this application requires considering the state of the auction (that is, which of the sequential auctions is being played), and reinforcement learning algorithms can take this into account. The verification of an approximate equilibrium becomes computationally more demanding for games with many players and stages. Yet, for a variety of multi-stage games, experimental results have shown that the approximation error to an equilibrium can be bounded by a small constant.

A word of caution is in order: Determining whether a pure strategy Bayes-Nash equilibrium exists in a normal-form game is NP-complete,¹³ and even for two-player normal-form games, finding an exact or approximate Nash equilibrium is PPAD-complete.¹⁶ These worst-case complexity results extend to Bayesian models with continuous types and actions; for instance, finding an exact Bayes-Nash equilibrium in a simultaneous second-price auction is PP-hard, and even approximation is NP-hard.¹⁰ However, these worst-case results do not mean that models with a small number of continuous actions and players cannot be closely approximated. Furthermore, game-theoretic models of markets are of particular value when the number of participants is small and participants can influence the price with their actions. So, while computational complexity is always a concern, machine learning can provide useful tools for many economically relevant models.

There remains the question as to understanding when we can expect learning algorithms to find an equilibrium. As occurs so often in machine learning, experimental research leads to impressive results, but providing ex-ante guarantees is thorny. Ex-ante convergence can be proved for single-item all-pay auctions in finite dimensions, where signals and bids are discretized.¹ Interestingly, known sufficient properties for convergence of learning algorithms, such as monotonicity of the game gradient, do not even hold in first-price auctions.⁵ The infinite-dimensional case, where continuity of valuations and bids is assumed, and the convergence of learning algorithms in other Bayesian games, remains an open problem. Generally, the theoretical analysis of learning dynamics in such games requires new techniques beyond those used for single-agent online learning. This constitutes a research frontier for theoretical computer science.³¹ However, even in the absence of ex-ante convergence guarantees, equilibria found via machine learning can be verified ex-post, which already enables equilibrium analysis in cases that were considered intractable thus far.

Designing Revenue-Maximizing Auctions

As a second opportunity for differentiable economics, we focus on the use of neural-network-based pipelines for the automated design of revenue-optimal single-stage auctions. The problem of finding a single-stage auction to maximize expected revenue, given equilibrium bidding behavior, is canonical to economic theory. The classic setting is that of selling a single item, where the auction designer knows the distribution on values of bidders. This single-item problem was solved by Myerson,³³ but more than four decades later no analytical solution is available for the problem of selling two items to even just two bidders. This comes from the suboptimality of selling each item separately, and indicates the analytical difficulty in modeling incentive constraints in solving the inverse problem.

As a computational problem, this can be formulated in domains with bidders with discrete values as a linear program of exponential size in the number of items and bidders, but new techniques are needed for large instances or settings with continuous values. Recently, new forms of machine learning algorithms have been introduced for solving problems of revenue-optimal auction design.¹⁸ These algorithms are based on neural networks, and they find approximately optimal designs in a wide variety of settings and represent the state of the art in computational methods for auction design. There were previously no methods for solving optimal auction design problems with bidders with continuous values while also requiring simple, dominant-strategy bidding equilibria.

While our focus here is on the problem of optimal auction design, differentiable economics has also been applied to other economic problems, including data markets,³⁹ second-best efficiency under budget constraints,¹⁹ and market-making in decentralized finance.¹⁴ In application to auctions, differentiable economics makes use of neural networks to represent the allocation and payment rule and a training pipeline to optimize these rules and compute approximately optimal designs. In an auction with multiple items $M$, each bidder has a value $v_i\left(S\right)\ge 0$ on each subset or bundle, $S\subseteq M$. For simplicity, we focus on sealed-bid auctions that correspond to single-stage games, and with players—here bidders—with valuation functions $v_i$ that come from independent draws from a distribution. An auction specifies an allocation rule, $g$, which maps the bids to a distribution on allocations, and a payment rule, $p$, which maps the bids to a payment for each bidder (or expected payment). The revenue-optimal auction design problem is to find a pair of functions $(g,p)$ that optimize expected revenue while achieving strategy-proofness, such that each bidder’s dominant strategy is bid truthfully. More general definitions allow for Bayesian incentive compatibility, so that truthful reporting is a Bayes-Nash equilibrium.¹⁹

A variety of neural-network-based algorithms have been developed for solving this problem. Following Wang et al.,⁴⁴ they vary (see Figure 3) as to whether they are:

• Expressive: Revenue-optimal auctions are in the function class represented by the neural network.

• Strategy-proof: The learned auctions have truthful bidding as an exact, dominant-strategy equilibrium.

• Multi-bidder: The framework is able to support multiple bidders.

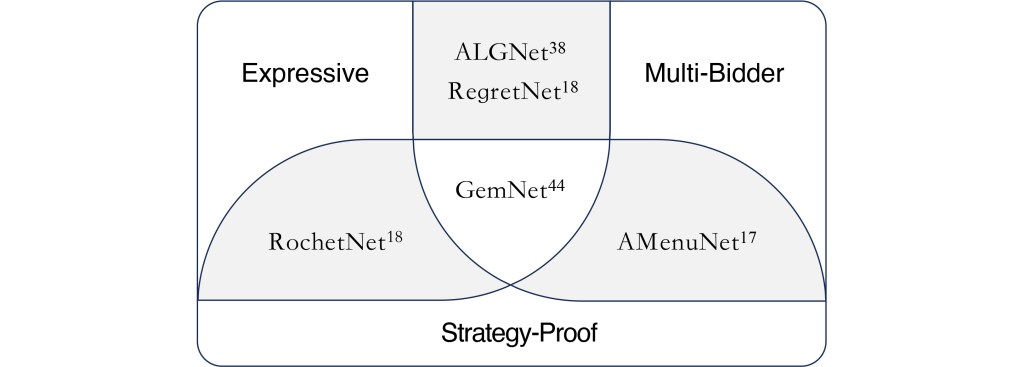
Even single-bidder auction design problems can be interesting. For example, when selling information goods that can be supplied in any quantity, a multiple-bidder problem is equivalent to solving multiple single-bidder problems (since there are no resource constraints to couple the problem across bidders). Still, multi-bidder problems with goods in limited supply, and thus technically quite different from single-bidder problems, comprise most of the industrial applications of auctions.

The methods in Figure 3 work by combining a particular network architecture, representing the rules $(g,p)$ of the auction via a parametrized neural network with a loss function. Inputs are sampled (valuation functions $v_i$) from a known distribution, with empirical loss minimized on these inputs via stochastic gradient descent. This loss may correspond to negated revenue, for example, or some combination of revenue and violation of strategy-proofness, in the style of Lagrangian optimization.^18,38

As an illustration, the RochetNet architecture¹⁸ works for a single bidder, with a network being learned to represent a menu of choices available to the bidder. Each choice corresponds to a randomized allocation of items and a price. Further, the network architecture determines the outcome of the auction for a given input (bid), and defines functions $(g,p)$, by choosing the menu element (from the learned menu) that maximizes the utility of the bidder, assuming the bid truthfully represents the bidder’s valuation function. This provides strategy-proofness. For example, given a bid $2 on Item $A$, $3 on Item $B$, and $5 on Bundle $AB$, and a learned menu $\left\{\right(\varnothing ,\$0),(A,\$2.50),(B,\$1),(AB,\$4\left)\right\}$, RochetNet would select as the outcome $(B,\$1)$ for utility $2 since this is utility-maximizing for the bidder. Crucially, 1) the menu is independent of the bid and fixed (“bid independence”) and 2) the optimal choice for the bidder is selected as the outcome of the auction (“bidder optimization”). Together they ensure strategy-proofness, since bids have no effect on the menu and bidding truthfully ensures the neural network optimizes for the bidder’s true utility function. In this way, the neural network encodes strategy-proofness. Revenue optimality is achieved by sampling from the value distribution and minimizing empirical loss, with loss defined as negated revenue. Hertrich et al.²⁶ give a theoretical justification for the success of RochetNet, proving that the network satisfies mode connectivity, where local optimal solutions (modes) are connected by simple paths in the search space.

GemNet⁴⁴ extends the RochetNet menu-based architecture to multi-bidder problems. As per Figure 3, GemNet is expressive, strategy-proof, and multi-bidder. The network now learns a different menu for each bidder and the menu for bidder $i$, any $i$, can depend on the bids of others but not bidder $i$’s own bid. This retains bid independence and is part of encoding strategy-proofness. The main challenge is to also provide bidder optimization—such that the outcome is utility-maximizing for each bidder—while ensuring that no item is ever allocated to more than one bidder. This is achieved through a two-step process. First, the loss function is defined to also incorporate an overallocation penalty during training. Second, there is a post-training menu transformation step, which uses a series of relatively small, mixed-integer linear programs to perturb the learned prices in the menus to ensure the bidder-optimizing choices never overallocate. The expressiveness of GemNet comes from the flexibility to choose a large enough network architecture (for example, enough hidden layers) as well as bid independence and bidder optimization being without loss in strategy-proof auctions. Earlier methods in automated mechanism design¹² make use of linear programming, but require solving a single optimization problem representing the entire multi-bidder auction design problem, scaling exponentially in the number of items and bidders. The mixed-integer linear programming subroutine in GemNet scales much better than these earlier global formulations because, in effect, it only represents a small sub-part of the problem representing prices on the menu choices as the input of one bidder varies (see Wang et al.⁴⁴).

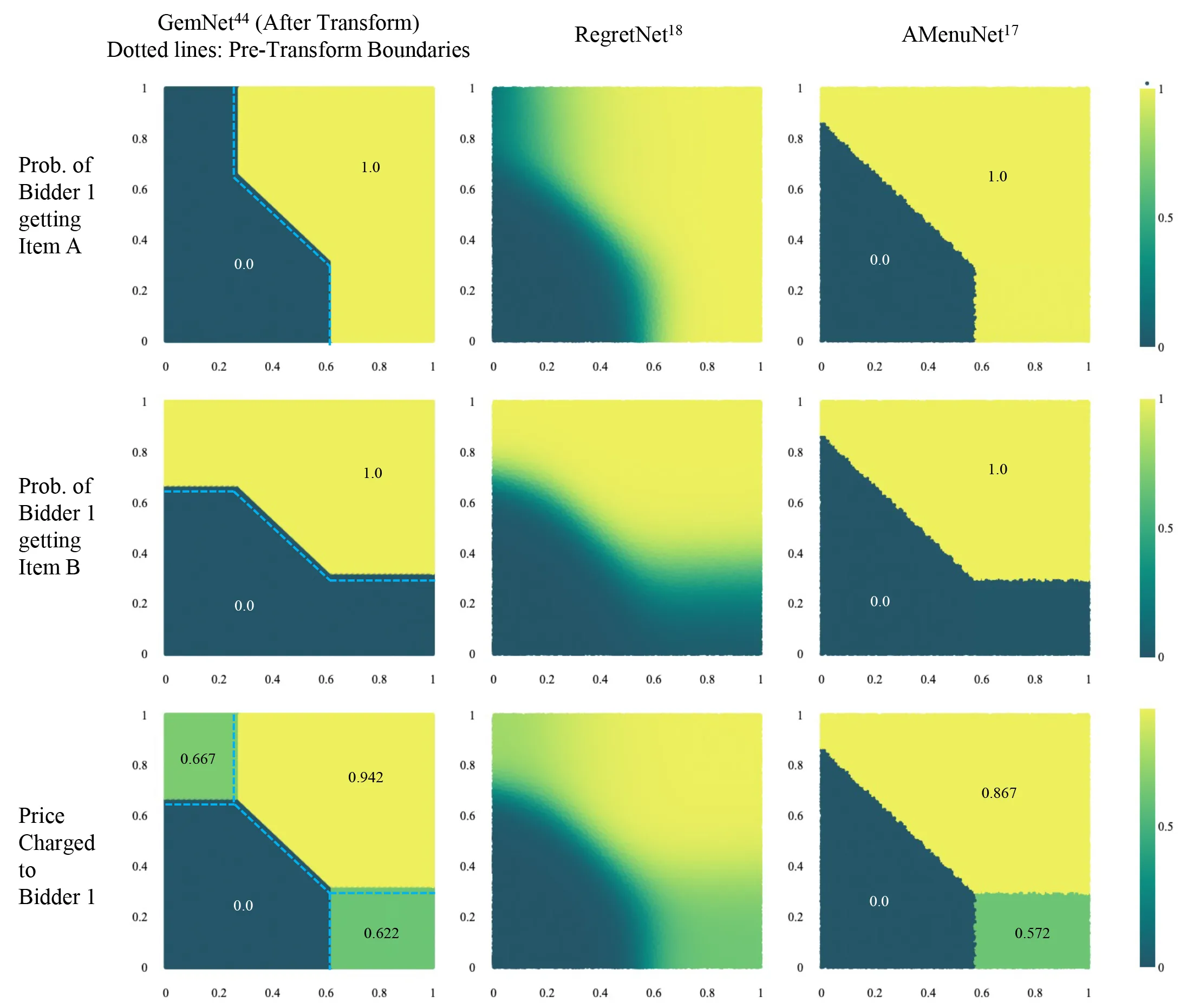
For an illustration, see Figure 4, which shows the results of using different methods of differentiable economics to design an auction for a problem with two additive bidders, such that a bidder’s value for Bundle $AB$ is the sum of their value for Item $A$ and Item $B$. In contrast to GemNet, RegretNet¹⁸ is expressive and multi-bidder but not exactly strategy-proof, while AMenuNet¹⁷ is strategy-proof and multi-bidder but not fully expressive. The comparison with RegretNet demonstrates the advantage of menu-based auction design, with clear and interpretable decision boundaries that can support theoretical understanding. The comparison with affine-maximization methods such as AMenuNet shows how the improved expressive capacity of GemNet leads to different mechanisms. GemNet also yields higher expected revenue than other approaches.⁴⁴

Although this use of differentiable economics for auction design shows much promise, there remain many interesting future directions and challenges, including the use of differentiable economics methods for the design of multi-stage auctions,^8,9,23,42 and the design of combinatorial auctions, for which current methods only apply to settings with just two items.¹⁸ There are also theoretical results on the sample complexity of the problem of learning revenue-maximizing auctions,^2,11,24 establishing a series of increasingly general results for learning approximately revenue-optimal, exact or approximately incentive compatible auctions with polynomially many samples. The more general results work with Bayes-Nash rather than dominant-strategy equilibria and focus on sample complexity but not computational efficiency.²⁴

Discussion

Differentiable economics describes a new approach to solving canonical problems in economics that take into account the incentives and strategic behavior of economic agents. These problems are computationally hard in the worst case, and analytical solutions to important equilibrium or mechanism design problems are only known for simple settings. Differentiable economics describes a learning-as-optimization paradigm that approximates solutions to specific, economically interesting problem instances such as auctions. In equilibrium problems, differentiable economics references the differentiability of the utility functions of agents resulting from the rules of a game, which then allows for learning algorithms that follow the utility gradients. In auction design, differentiable economics references that the rules are represented in a differentiable way via neural networks and allows for learning algorithms that follow the revenue gradient.

Recent results in differentiable economics suggest learning algorithms may converge to an equilibrium in many canonical settings from economics. Given that equilibrium learning algorithms converge to equilibrium in so many models of auctions and price-based markets, they also provide an effective means to compute equilibria and provide comparative statics in environments that have long been assumed to be intractable. The new techniques allow for various types of utility functions (for example, with risk aversion or regret) and different distributional assumptions. Such flexibility can help analysts develop more realistic models and vastly speed up the analysis.

Even if learning algorithms fail to converge, the analysis of learning dynamics may provide a better characterization of the game than an intractable fixed point.³⁵ Such cases, with failure of convergence, also call for market and mechanism design to change the game dynamics. As we show here, machine learning can also be used for these inverse problems, giving a versatile method for the design of new mechanisms with simple, dominant-strategy equilibria.

This article contributes to a longstanding discussion about the interaction of game theory and artificial intelligence,⁴³ but emphasizes the power of machine learning and how recent advances help in solving longstanding problems in economics. Machine learning can also be used to develop new theories for how humans play games,⁴⁵ holding promise in allowing behavioral economists to better understand and model human behavior. We argue that machine learning can lead to a paradigm shift and significantly expand the scope of strategic situations that we can analyze and design.