Abstract
Side-channel attacks, such as Spectre, rely on properties of modern CPUs that permit discovery of microarchitectural state via timing of various operations. The Weird Machine concept is an increasingly popular model for characterization of execution that arises from side effects of conventional computing constructs. In this work, we introduce microarchitectural weird machines (µWM), code constructions that allow performing computation through the means of side effects and conflicts between microarchitectual entities such as branch predictors and caches. The results of such computations are observed as timing variations in the execution of instructions that interact with these side effects. We demonstrate how µWMs can be used as a powerful obfuscation engine where computation operates using events unobservable to conventional anti-obfuscation tools based on emulation, debugging, and static and dynamic analysis techniques. We present a practical example in which we use a µWM to obfuscate malware code such that its passive operation is invisible to an observer with full power to view the architectural state of the system until the code receives a trigger. When the trigger is received, the malware decrypts and executes its payload. To show the effectiveness of obfuscation, we demonstrate its use in the concealment and subsequent execution of a payload that creates a reverse shell. In the full version of this work, we also demonstrate a payload that exfiltrates a shadow password file. We then demonstrate the generality of μWMs by showing that they can be used to reliably perform non-trivial computation by implementing a SHA-1 hash function.
1. Introduction
The ability to model and classify a program’s behavior is fundamental for a vast number of security related tasks. It requires a form of emulator which implements a reference model of the target machine.
If this model deviates from the actual machine’s behavior, key properties of many security mechanisms are violated. This can be exemplified by a proof-carrying code framework1 that allows an arbitrary untrusted executable to run securely on a target platform. Security is established by the target system checking a proof provided along with the executable. The proof ensures the executable cannot perform any activity (or computation) outside of a formally specified policy. Any deviation between the expected and actual target system behavior effectively violates the proof.
Many security mechanisms are based on either guaranteeing that the program (1) cannot perform an action from the deny-list, or (2) can only perform actions from the allow-list. Examples of such mechanisms include model checking, formal verification, taint analysis, control flow integrity enforcement, malware detection and sandboxing.
Program obfuscation2 is the general problem of transforming programs to prevent reverse engineering or other forms of analysis. While it is commonly used to hide malware, it can also be used to conceal benign sensitive code in proprietary applications8 or to improve security.6 A strong obfuscation engine can be constructed if the obfuscated program utilizes features of the target platform that are outside of platform’s reference model used by the analyzer.
Recently a number of papers introduced the concept of weird machines (WM)5,7,9 to formalize certain classes of exploits. According to this concept an exploitable vulnerability not only provides access to otherwise protected data but creates a new computational model within the original program. Such models exhibit emergent behaviors that are complex and not intended by the original system design, often violating fundamental security properties. Weird Machines based on this model can be programmed and programming is achieved with data that is passed to the vulnerability.
WM primitives can be utilized as powerful obfuscation engines. Previous research demonstrated the presence of such primitives in common implementations of various software and hardware components. Programming these WMs does not require vulnerabilities. For instance, Turing-complete WMs were built utilizing little known artifacts inside the page-fault handling hardware,3 ELF-loader16 and exception handler14 mechanisms. These WMs have inherent obfuscation capabilities. They use features of computer systems that are not identified as dangerous by antimalware software and they are naturally difficult to analyze. To the best of our knowledge, no universal WM detection approach has been proposed.
In this paper we establish a new type of WM implemented using microarchitectural (MA) components of a CPU, their complex inter-component interactions and how they affect the latency of common operations. We call such machines WMs (short for microarchitectural weird machines). At a high level, the computation is performed by executing regular instructions such as memory loads and stores, jumps and conditional branches and observing execution time. The WM is constructed from three types of abstract components. Weird registers (WRs) are data storing entities implemented using states of MA components. Weird gates (WGs) are basic computation components which transform data stored in WR according to their logic. WGs utilize entanglement of various MA component states and their side effects such as aliasing, evictions and speculative execution. Weird circuits (WCs) are ensembles of WGs and implement more complex logic. We demonstrate that the proposed computation framework can be used to perform general purpose computations.
Since reverse engineering and binary analysis tools do not emulate MA components, we believe that our framework can be used as a universal approach for program obfuscation. Moreover, even if detection tools include the MA layer of the system in their reference model, we argue that precise detection of WM computations is challenging due to their natural flexibility and differences across CPU architectures. In addition we discuss how we found several surprising ways for WMs to improve security. We believe that this paper introduces a new research area by looking at components responsible for MA attacks from a different angle and studying them from the perspective of computation artifacts.
2. Background and Motivation
All current processors can be specified at the architectural and microarchitectural layers. The architectural layer is defined by the ISA and represents the machine state composed from CPU registers, instruction pointer and addressable memory. Programs interact with it directly by executing instructions. It is well documented and can be formally specified.13 This layer is implemented by internal microarchitectural components that compose the microarchitectural layer. This layer is not directly accessible to programs. Modern day CPUs incorporate a large number of performance optimization mechanisms such as caches, prefetchers and various buffers. Many of these mechanisms have internal data structures with a complex state space.
While the presence of these mechanisms is a well known fact, little data is available on their internal structure and operation apart from the textbook-level description. Moreover, outside of their effects on the execution time, these mechanisms are completely transparent to programs executing on the CPU. Yet, programs are capable of implicitly manipulating MA components by performing regular activity. This property is used in traditional MA side channel attacks. For instance, a memory access having an address dependency on sensitive data triggers a change of state inside the CPU cache. The attacker can then probe the state and infer the secret data. This basic principal forms the foundation of WMs.
2.1 WM use cases.
Considering the diverse range of applications for program obfuscation, including non-offensive purposes, (WMs) can be utilized in various scenarios. Below we present a selection of these use cases.
Hiding malware. Malicious functionality in sensitive applications can be easily obscured by implementing it using WMs. Malware can avoid being detected by dynamic or static analysis tools if code sequences used in malware are implemented using WMs. Moreover, doing so provides strong anti-debug protection since MA state is not visible by a regular debugger and is highly volatile. For the same reason WMs can be used to implement a logic-bomb or trojan application12 which appears benign but activates its malicious functionality when triggered.
Preventing reverse engineering. Obfuscation techniques can be used to prevent reverse engineering applications for protection purposes. For instance, software developers may want to execute a secret algorithm on a third party untrusted machine without disclosing the algorithm’s internals. WMs can be used for this purpose since reverse engineering requires understanding of complex MA effects which is a difficult task as we demonstrate later in this paper.
Preventing emulation. WMs exploit unique features of a CPU’s internal components and their interactions such as address conflicts and race conditions. Emulating such effects with acceptable precision is extremely difficult as it would require accurate reverse engineering of the target hardware platform. Currently existing cycle accurate simulations only provide an approximate performance model and do not contain the level of detail required to emulate WMs. We propose to use WMs as an emulation detection/prevention tool where computation can only be performed on real hardware.
Violating formal proofs, sandboxes, taint analysis, preventing forensics. Since currently existing analysis tools do not model the MA layer, WMs can be used to perform activity outside of the security model. In addition, since WM’s current state is not located in regular memory but instead is encoded in the state of MA components, traditional forensics tools cannot be used to study WMs.
2.2 Program obfuscation and the microarchitectural layer.
To illustrate the problem of program obfuscation, we consider two entities: the obfuscator and the detector. The obfuscator’s objective is to perform a desired computation, often with malicious intent, while evading detection. The detector aims to determine whether the target program executes or has the capability to execute such a computation. Please note we use the term “computation” in a broader sense, referring to a sequence of actions or state transitions performed by a machine. A detector needs monitoring capabilities such as the ability to execute a target program, pass data and observe a machine’s state. Consequently, the obfuscator’s goal is to modify the desired computation to circumvent specific conditions that a detector searches for. In traditional obfuscation techniques this is often achieved through a variety of code transformation techniques.4
The effectiveness of a detector relies significantly on the extent of its monitoring capabilities. A highly advanced detector can possess complete visibility into the program’s memory and registers, allowing it to single-step the target program and accurately model the behavior of the underlying machine. While accurately modeling the machine’s behavior at the architectural layer is achievable, modeling all aspects of the microarchitecture is currently infeasible.
Considering this, the microarchitectural layer emerges as a promising candidate for constructing an obfuscation framework. First, it provides a rich state space due to numerous structures implemented at the MA layer. Second, MA states are affected by programs executing on the machine, making it programmable by executing regular code. Third, the MA layer is usually not well documented, making it very difficult or impossible to create a perfect model.
Later in the paper we demonstrate how simple elements of the MA can be discovered, modeled as finite-state machines (FSMs) and manipulated to create basic computational primitives. Note that it is not necessary for this model to be a complete and full representation of the MA layer. Instead, the attacker can reverse engineer only a few components and manipulate them to evade detection.
Speculative execution is a common feature in processors which allows the CPU pipeline to perform conditional computations before the values of the conditions are fully determined. In particular, the pipeline relies on predictions from components such as branch predictors to guess the most likely instruction sequence and executes it immediately. If the prediction later is deemed incorrect, the CPU performs a roll-back and continues execution with the correct instruction sequence. However, during such erroneous execution, instructions from the mispredicted instruction sequence are allowed to make changes in MA components. This feature provides unique functionality for constructing WMs. It allows the creation of a divergence between the architectural and microarchitectural state of the machine. In particular, to implement a WM, the malicious executable may intentionally trigger a branch misprediction causing some instructions to be erroneously executed in speculative execution mode. Due to the eventual roll-back these instructions will not trigger any state changes at the architectural layer, however they will cause state transitions at the microarchtiectural layer. As a result, an analyzer with full visibility of the architectural state of the machine cannot detect malicious computation if its critical components are implemented via MA state transitions during an erroneous speculative execution.
3. Weird Registers and Gates
In this section we introduce the concepts of weird registers (WRs) and weird gates (WGs), basic building blocks for constructing WMs. The former are used to store data during the WM’s computations and are constructed from implicit manipulations of microarchitectural components. The latter represent a minimal functional unit of the WM, processing data in its registers.
3.1 Weird registers (WRs).
Any machine or subsystem thereof that has computational capabilities can be formalized as an abstract finite state machine , where is a finite set of states, is the input alphabet, and is a transition function. Each state represents a unique configuration of all of the machine’s internal components. While this level of detail may seem impractical, it is possible to simplify complex FSMs by limiting the number of observable states. This simplification creates a new FSM with a reduced number of states, input symbols, and a simpler transition function. However, this simplified FSM still encapsulates the computational logic inherent in the original machine. For instance, if the focus is on analyzing cache events, it may be beneficial to consider analyzing the cache FSM rather than treating the entire machine as an FSM.
We refer to such simplified FSMs as sub-FSMs or sFSMs. These sFSMs are employed to capture and represent specific behavior within a more complex system. We utilize these sFSMs to construct simple computational devices that will be used for obfuscation. Specifically, they are utilized to implement data storage primitives represented by WRs and computational primitives represented by WGs. We begin our discussion with explaining the construction of a WR.
By definition, a sFSM does not have full information about the original machine but it is useful for analyzing a specific aspect of the machine. Suppose there is a MA resource that we want to utilize as a storage entity and construct a WR , for example the CPU data cache. We first select some variable, var, in the program’s memory. Then a simple sFSM can be defined with a small set of observable states . For instance, we reduce the state space associated with var to only two states. Let those states be . is in state when var is not cached and is in when var is cached. It is possible to construct a more intricate FSM by taking into account other aspects of the cache such cache level and Least Recently Used (LRU) status. We choose not to do so in this work. The state transition logic for this sFSM is simple. When the variable var is accessed, the transitions to state . When var is flushed from the cache through the execution of the clflush instruction, the sFSM transitions to state . These transitions occur irrespective of the current state of the sFSM. This establishes the input alphabet for . In particular, flush(var) and access_mem(var). Then accepts symbols of this alphabet and triggers state transitions as previously described. This allows us to implement a weird register, a basic 2-bit microarchitectural storage primitive which uses the CPU data cache for storage. We refer to this register as DC-WR for “data cache weird register”.
The state of the DC-WR is read by timing the number of CPU cycles it takes to access the chosen memory location. Please note that reading DC-WR register state is an invasive operation. It causes to transition to state . Therefore we introduce an additional signal, read(r) for the corresponding sFSM. Processing the read instruction (passing ) causes the same state transition as previously defined but has the side-effect of storing the access time in a CPU register. We define to have a logic value of 0 when it is in state (not cached) and to have logic value 1 when it is in state (cached). It takes fewer CPU cycles to load var when it is in cache. Therefore we determine the logic value of by executing the read(r) instruction which has the side-effect of placing that timing in an architecturally visible CPU register. If the load time is greater than a certain threshold logic 0 is registered, otherwise it is logic 1.
L1 cache state is one of many computer subsystems that has microarchitectural resources that can be explicitly or implicitly manipulated into states that can be made architecturally visible by means similar to the DC-WR. We show some examples of WR that can be constructed using these other subsystems in Table 1. In addition to utilizing MA subsystems that have internal storage functionality, WRs can be implemented through modulating contention on MA resources. Examples of such WRs include registers based on mul instructions and the Reorder Buffer (ROB) listed in the table.
| Primitive | Write bit (0 or 1) | Read bit |
| d-cache | 0: clflush(var), 1: ld var | measure cycles to access variable |
| i-cache | 0: flush(code), 1: call code | measure cycles to execute code |
| ROB contention | 0: execute nop instructions, 1: execute instructions with dependencies | execute any instructions and detect stalls |
mul func. units | 0: execute nop instructions, 1: execute mul instructions | measure cycles to execute mul |
| Branch direction predictor11 | 0: train conditional branch to predict non-taken, 1: train conditional branch to predict taken | execute branch non-taken and measure cycles |
| BTB10 | 0: execute jmp from A to B, 1: execute jmp from A to C | measure cycles to execute jmp from A to B |
| Intel VMX | 0: execute nop instructions, 1: execute VMX instructions | measure cycles to execute a single VMX instruction |
The concept of a WR can also be applied to formally analyze microarchitectural covert and side channels.18 To construct a covert channel the sender and receiver repeatedly write and read the same WR. A side channel is formed when a victim program unintentionally writes to a WR which is subsequently read by an adversary. We believe that many microarchitectural covert or side channel can be abstracted as a WR and therefore can potentially support WM execution.
In addition to the data storage capabilities, WRs possess distinct properties that prove valuable in the context of obfuscation.
Volatility. many states of microarchitectural entities are ephemeral in nature and exist only for a brief duration. For example one can create a WR from two states of a limited pipeline resource, such as a multiplication unit which can be in two contention states, high and low. This register will hold its value for several cycles and then default to the value associated with low contention.
State decoherence. reading a WR can destroy its value since the reader interacts with the MA resource, for example by accessing memory and measuring the latency. Note, that other normal system activity can also interfere with the corresponding MA resource and destroy data in the WR. This property makes it challenging for a potential analyzer to observe WM’s state and apply forensics techniques.
Entanglement. many MA resources are intricately interconnected, often in non-obvious ways. For instance, assigning a value to a data cache based WR requires the execution of code, for example, a mov instruction. This in turn triggers activity in the instruction cache. Consequently, interacting with data cache WRs can have an impact on other WRs implemented using instruction cache. While this may initially be perceived as unwanted side-effect, such interference gives rise to distinctive emergent properties. We leverage this property later in the paper to construct WCs.
3.2 Weird gates (WGs).
The Weird Gate abstraction builds on that of the WR. WGs are basic elements of computation that exploit connection between different MA entities and their corresponding WRs. A WG is a code construction that implicitly invokes an activity in MA components in which the state of one or more WR (input WR) conditionally changes the state of one or more WR (output WR) thus performing computational logic. The WGs we discuss in this paper can be viewed as the implementation of logic gates such as AND, OR, and NAND. The WG abstraction includes more complex constructs that do not necessarily have two level logic output. We have experimentally verified operation of such gates, but we choose to leave their description to future work. Among the WGs for which we provide experimental results in Section 6 are NAND gates. This suffices to demonstrate universality of WGs as it is known that any arbitrary logic gate may be constructed using NAND gates. We have proofs of Turing Completness of WMs that fall outside the scope of this article.
3.2.1 Weird AND gate.
One of the simplest WGs we demonstrate in this paper is a gate that implements a logical AND operation which ANDs two input weird registers. In particular, we use WRs implemented based on the branch predictor and instruction cache as input. The WG’s pseudocode and operation flow-chart are presented in Figure 1. Please note that for simplicity we combine gate code together with input WR assignment operations in a single function. In real WMs these will be performed separately. The operation of the gate is based on the following set of observations. The branch predictor can either correctly or incorrectly predict the direction of a conditional branch instruction. This depends on the branch direction history. When the direction is incorrectly predicted, erroneous speculative execution is activated. It is possible to intentionally mistrain the branch predictor to do so at a desired time. One can make a branch execute in the taken direction multiple times followed by a single execution in the not-taken direction. During the final execution, the branch predictor mispredicts and triggers erroneous speculative execution. To prevent the CPU from detecting the misprediction and terminating speculative execution quickly, the data that is used for determining branch direction must be evicted from cache. There is another condition required for speculative execution to proceed. The code from the mispredicted direction of the branch must be in instruction cache (IC). Otherwise, the CPU will generate an IC miss and wait for the code to become available. If the delay is long enough, the branch misprediction will be detected and speculative execution terminated in the meantime. On the contrary, if the code is in IC, these instructions will execute and change the MA state. This race condition enables the implementation of fundamental conditional logic and serves as a fundamental building block for WGs.
AND WG (a) and its workflow (b).The first input weird register for the gate is a WR implemented using the branch predictor state associated with the gate’s if statement (line 11). We refer to it as BP-WR. The BP can be trained into one of two states. In state 0 the BP will be trained to not speculatively execute a block of code (line 14). In state 1 it will execute the code. In the pseudocode from Figure 1, setting the BP-WR to state 1 is shown as train_bp_nt(). The NT stands for not taken, training the branch predictor to the not taken state causes the speculative block to be executed. train_bp_t() sets the BP-WR to 0 since the BP taken state causes the speculative code to not be executed. Our Weird AND gate uses this BP-WR as one of its two inputs.
The output of our AND gate is in a DC-WR associated with a variable out_c. The body of the if statement (not taken branch) contains a memory access to this variable. If the BP-WR is in state 1 then the speculative execution is activated, and the state of the DC-WR will be set to 1 (in cache). We always set the DC-WR to 0 by flushing out_c from cache prior to gate execution.
The second input WR to our AND is an instruction cache WR (IC-WR). The code for the speculative block containing the DC-WR access is either in the instruction cache (state 1) or that code is not (state 0). Due to the limited duration of the speculative window, if the code is not in the IC then it will not be executed. When we combine these two input WRs we see that the DC-WR memory access will only occur if both BP-WR and IC-WR are set to 1.
Note that the operation of this gate is architecturally invisible. While the inputs and outputs are visible, the actual AND logic makes no call to any kind of CPU AND instruction. The part of the WG that modifies the DC-WR state only occurs in speculative mode which has no architecturally visible effects.
3.2.2 Other weird gates.
Using the approach presented above it is possible to implement other logic gates. For instance, the AND gate can be converted into an OR gate if the code is modified in such a way that triggers memory access to the variable out_c when either code is cached in IC or when the branch predictor is properly trained. For more details please refer to the full version of our paper.
In addition to the aforementioned gates, we composed and studied other logical gates. We were able to create several kinds of gates that work with a high degree of accuracy. Table 2 provides an overview of performance and accuracy for a representative sample of such WGs. Note, the table also includes TSX-based gates that we discuss in the next section. We provide additional evaluation details in Section 6.
| Weird Gate | Iterations | Execution Time (s) | Executions / Second | Accuracy |
|---|---|---|---|---|
| AND | 1M | 15 | 66,666 | 100% |
| OR | 1M | 57 | 17,543 | 98% |
| NAND | 1M | 13 | 76,923 | 100% |
| AND_AND_OR | 1M | 81 | 12,345 | 99.4% |
| TSX_AND | 1M | 0.591 | 1,692,047 | 98.5% |
| TSX_OR | 1M | 0.591 | 1,831,501 | 97.9% |
| TSX_ASSIGN | 1M | 0.42 | 2,380,952 | 98.5% |
| TSX_XOR | 1M | 16.6 | 60,020 | 99.2% |
4. Weird Circuits (WCs)
WGs described in Section 3.2 enable a basic framework for constructing WMs. A computation is first expressed as a boolean circuit and then divided into a sequence of individual register and gate operations. This model of operation requires the outputs of each gate to be read from the output register into the architectural state of the program before it can be sent to the next gate’s input. For the WRs implemented using the data cache, reading the intermediate state is done by measuring the load time in CPU cycles to access the corresponding memory location via the rdtscp instruction. Then the state is written into a WR that is used as input for the next gate. There are several disadvantages to this approach. WR reading and writing operations require adding instructions to the base program which reduces performance. Moreover, WM composed in such a way are less suited for obfuscation since the intermediate state of the WM is stored in architectural memory. An advanced analyzer may be able to detect malicious patterns in state transitions of the architecturally-visible program or inside the program’s memory.
Both of these limitations can be addressed by performing contiguous computation within MA state instead of using architectural state to enable the dataflow between weird gates. The goal is to enable contiguous ensembles of WGs that implement more complex binary functions than individual gates without saving the intermediate state in architecturally-visible memory. We refer to such ensembles as weird circuits (WCs). In a WC, data is copied into the MA layer only once and then a series of WGs are activated in such a way that the output of one gate serves as input for another gate. The intermediate data is stored inside WRs for the duration of the WC activation.
To describe how WCs are formed and operate consider a minimal WC consisting of two AND gates connected in series and implementing a binary expression c = a & b & a. Assume WRs a, b and c are implemented as in Section 3.2.1. Since a and b are purely input WRs and c is a purely output WR, the binary expression can be rewritten in the following way: c = a & b; b = c; c = a & b. In this way the binary expression is translated into a sequence of basic operations, individual gate activations and WR-to-WR transfers. To make this computation possible without copying the intermediate state into the architecturally-visible memory our WC needs to have two properties:
P1: Individual WG operations need to be contiguous. This means that activating a gate one time does not affect its consequent behavior.
P2: Transferring values between different registers must be possible to exchange values between input and output registers.
Previously described WGs lack both of these properties. First, the gates use branch predictor mistraining to activate erroneous speculative execution required to create the necessary race condition. The mistraining becomes challenging for multiple consequent gate activations. Modern branch prediction units (BPUs) are known for accurately predicting complex branch patterns. When the WG code attempts to repeatedly mistrain a certain branch, the BPU quickly learns this pattern and begins predicting the branch direction correctly. This violates P1.
P2 cannot be fulfilled due to the use of WRs of different types and the lack of hardware interfaces to transfer the state between separate MA entities. For example, consider a case when we need to assign the value of c implemented as a DC-WR to another WR b, implemented as a BP-WR. In this case, we need to conditionally train the BPU depending only on the state of another MA entity, the data cache. Unfortunately there is no simple way to achieve this. At the same time, transferring the state within a single MA entity appears possible. Suppose we have two DC-WR e and f implemented using variables d0 and d1 correspondingly. By storing the address of d1 in d0 we can implement a basic WR assign functionality (e = f). It is done by simply dereferencing the pointer (*d0) while in speculative execution. Under the race condition, variable d1 will be accessed only if d0 is cached enabling the conditional assign operation.
To overcome these challenges we need to implement a new WG mechanism that does not rely on BPU mistraining and uses WR of the same type for all input and output gates. While alternative implementations are possible, for this paper we will focus on the WCs we implemented based on Intel Transactional Synchronization Extensions (TSX) technology. Introduced in the Haswell microarchitecure, TSX provides CPU-level transactional memory operations using XBEGIN, XEND, and XABORT instructions. When a running program issues the XBEGIN instruction the CPU enters a transactional mode in which operations are executed until either the XEND instruction is encountered or an error condition occurs. When the CPU encounters an XEND instruction with no error then all effects from execution (such as memory reads and writes) are committed and become visible on the architectural level. If an error or fault occurs during the transaction then the executed code is rolled back such that there are no architecturally visible effects and the CPU continues execution at an address specified as an argument to the XBEGIN which is typically a fault handler.
However, as indicated by prior work,15 the execution is not stalled immediately. The pipeline continues to execute instructions even after the fault. This introduces a new source of speculative execution which we utilize for WG construction. MA side-effects from this speculative execution are not rolled-back upon leaving the TSX code. There are many conditions that will cause a TSX transaction to abort such as page faults and divide-by-zero operations.
We create a window of speculative execution simply by including a divide-by-zero error in each TSX block. In our experiments we observed that the transaction blocks exhibit a longer and more stable window of speculative execution than BPU mistraining. At the same time multiple TSX based WG can be strung in a row such that they compose a more complex WC that performs calculations in a serial fashion with no architecturally visible intermediate results. They also make it impossible for standard debugging techniques to be used for observing the operation of a TSX based WC. A requirement of the transaction interface is that no part of the transaction become architecturally visible unless the entire transaction completes with no other thread accessing memory used in the transaction. If an external debugger were to be able to observe what was happening in a transaction block that would by definition be a side-effect and would cause an abort. The debugger would see the XBEGIN instruction, then the next instruction would be the beginning of the abort handler.
Our TSX-based weird gates are based on the observation that the duration of speculative execution occurring inside a TSX code block upon a fault is limited. This creates a race condition. Assume a code sequence consisting of three instructions, i1-i3, that are executed inside a TSX transaction block with a fault. In this case, whether or not these instructions have a chance to execute and alter the MA state depends on their performance. For instance, if instructions do not have any memory dependencies, their execution time is low and they are likely to be executed. If they require data from RAM their execution time is unlikely to fit inside the speculative window. This phenomenon creates a basic primitive needed to construct logic gates. We can introduce dependencies between instructions by grouping them using arithmetical operations. For example, in the code sequence below the last instruction will be able to issue a store request and modify the MA state only if variables d0 and d1 are both cached. This effectively creates an AND weird gate with DC-WR registers as input and output.
i1: mov d0, %r1;
i2: add d1, %r1;
i3: mov (%r1), %r2;Figure 2 contains pseudocode for a sample TSX WC which simultaneously calculates two logical operations, AND and OR, in a single WC based on the principle that cache status of operands to addition will determine whether the addition will be performed. In this pseudocode d0..d4 are variables that implement DC-WRs. Absence from cache representing logic 0 and presence in cache is logic 1. Line 2 initializes all the DC-WR to logic 0 by flushing the memory to which they point. In lines 3 and 4 the architecturally visible inputs A and B are read into d0 and d1. The division-by-zero guarantees that the code inside the TSX block will execute inside erroneous speculative execution mode. Lines 8 and 9 implement the OR logic of the WC. If either d0 or d1 are cached (logic 1), the CPU will be able to calculate the address pointed to by d3 and dereference it during the speculative execution window. If both of them are not cached (logic 0), speculative execution will terminate before the memory access begins. Note that the architectural value stored at addresses pointed by d0 and d1 can be set to 0. Line 10 implements the functionality of logic AND. To successfully make a memory access to the address pointed by d2, both of the input WRs must be cached (logic 1).
After the WC has executed we read the WR values into visible memory. We want to avoid having the rdtscp instructions visible to an observer. We therefore perform the timed memory load inside a TSX transaction. An adversary attempting to observe the process of reading the WR will cause that transaction to abort which destroys the value of the WRs and leaves the architecturally visible outputs Q0 and Q1 set to 0. Intentionally causing such aborts to disrupt malware weird circuits hidden in a legitimate program is an interesting line of future work. It will, however, interfere with proper execution of the legitimate program if done in a naïve way.
We implemented a number of different logic gates using the TSX approach. A list of these gates and their performance data is shown in Table 2 including the XOR gate. The XOR gate is specifically useful as it can be used in simple one time pad (OTP) schemes to encrypt/decrypt data.
5. Applications of Weird Circuits
In previous sections we explored the design and implementation of simple weird circuits that demonstrate the ability to create functionally complete microarchitectually invisible boolean weird circuits. In this section we will first demonstrate weird obfuscation, a malware obfuscation system that uses a more complex WC. We will then examine in greater depth the multi-gate TSX-based weird XOR circuit used by the weird obfuscation system. Finally we will demonstrate an implementation of SHA-1 that uses weird circuits.
In this section we describe the operation of our weird obfuscation (WO) system and how we use this system to obfuscate malware code. We show that the malware’s passive operation is invisible to an observer with full power to view the architectural state of a system until the code receives a ping with a special trigger value in the body. When the trigger is received the malware decrypts and executes its payload. We will demonstrate the use of our WO system to conceal and then execute a payload that creates a reverse shell. In the full paper we also demonstrate shadow password exfiltration.
In our scenario we are in the role of an attacker who has managed to get an advanced persistent threat (APT), such as a trojan horse, installed onto a computer running inside an adversary’s network. Our adversary, the defender, has the ability to view all architectural state of the infected computer. Our adversary has the power to run our infected program in a debugger or other dynamic analysis tools. We hope this work will inspire future work for development of static analysis tools that will detect and characterize WM in programs such as our APT, but as discussed in Section 1 those tools do not yet exist. We therefore do not give our adversary abilities granted by those theoretical tools.
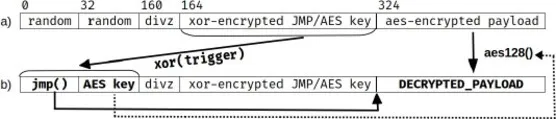
When constructing our APT we first take the payload, choose a random 128 bit AES key, encrypt the payload with that key and store the encrypted payload in the structure shown in Figure 3 a) starting at bit 324. We then place a specially crafted jmp instruction at bit 164 followed by the AES key. Next, we create a random one-time-pad of length 160 bits and XOR each bit of the pad against the bits of the memory structure starting at bit 164. This has the effect of “encrypting” the jmp instruction and the AES key against the one-time-pad. The 160 bit one-time-pad will later be used as the trigger value that will cause our malware to enter its active phase. We complete the preparation by filling the first 160 bits of the structure with random data followed by an illegal divide by zero instruction, then copying the entire structure into the body of a TSX block.
wm_apt layout a) at start, b) after valid trigger.Our APT is malware hiding in a program that receives pings. Each ping body is used as an XOR key to transform the memory labeled xor-encrypted JMP/AES key in Figure 3 and overwrite the bits labeled random. Bits 32-160 are then used as an AES key to decrypt the payload at the end of the memory region. Finally, the entire region is mmap’d and executed inside a TSX block. If the secret key in the ping body was correct it creates a jmp instruction leading to the target function that will begin execution of the decrypted payload. When the pad and AES keys are correct the payload will execute properly and open a reverse shell to the attacker.
During the silent phase, before the attack is triggered, the affected machine may receive many pings. When a received ping does not contain the trigger value, the first 160 bits of the TSX block will contain a bad AES key resulting in garbage values in the decrypted payload, and no jmp instruction. Instead of properly jumping over the contents of the AES key and divide-by-zero instruction, this incorrectly-decrypted region is executed as-is. This will generally cause a near-immediate fault, but is guaranteed to fault by the time it reaches the tmp = tmp/0 instruction at bits 160-164. This fault is then rolled-back since it is inside a TSX block, and the program continues to wait for the next ping trigger.
All critical parts of this APT operate in TSX blocks which are not directly observable by a debugger. In addition, the one-time-pad “decryption” of the AES key is performed by a TSX-based XOR WG that has no architecturally visible intermediate values. The analyzer will not see any part of the payload until the trigger has been successful and the payload is already running.
Execution of the logic gates underlying the TSX-based XOR, as previously discussed, is not 100% accurate. Practically this means that each trigger must be evaluated by the APT multiple times. We chose this evaluation multiple to be 10. In our implementation the APT is able to process pings in real-time with inter-arrival times up to 500ms. Table shows the distribution of the number of pings required to successfully decrypt and execute the reverse shell malware payload in 100 experiments. It takes on average 6 attempts (6 pings) to successfuly XOR all of the 160 bits and execute the payload.
5.1 SHA-1 implementation.
We chose a hashing algorithm to be an illustrative high level algorithm with which to demonstrate partially architecturally visible WM for a number of reasons. A cryptographic hashing function provides a challenging case for WM which have components with less than 100% accuracy. Due to the nature of cryptographic hashes, single bit errors that occur during computation are magnified which makes SHA-1 a challenging test case. Another reason we chose a hashing algorithm is that our WC version can be used to replace the hash function in the architecturally visible malware obfuscation system due to Sharif et al.17 on which one of our example WM-based malware obfuscation systems is loosley based.
We call our our SHA-1 implementation “partially architecturally visible” because, while many interim values are stored in architecturally visible memory, all of the actual SHA-1 computation is performed by WM. For example, when the algorithm requires adding two numbers, no CPU add instructions are executed. The implementation performs the addition using a full adder constructed from two discrete weird XOR gates and a composed weird AND_AND_OR gate. During execution the output of the weird XOR gates is temporarily stored in memory as is the output of the weird AND_AND_OR. In out initial implementation, 41.9% of the intermediate results were architecturally visible.
As discussed in previous sections many of our weird gates have a high degree of accuracy, but in very long runs errors do occur. Our SHA-1 implementation uses redundant gate executions to provide the requisite accuracy. This is explained in greater detail in the full version of this work.
We ran a series of 10 experiments in which each experiment consisted of an execution of the SHA-1 implementation. For these experiments we chose conservative redundancy paramaters favoring accuracy over speed. Each of those experiments produced a correct hash. Each execution took around 26 minutes.
6. Evaluation
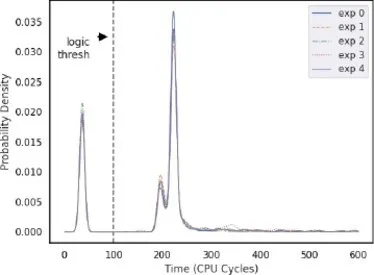
In this article we give a brief summary of our evaluation of some WGs and WCs we constructed. Details of methodology and further results appear in the full paper. One of the challenges for a developer programming with WGs is that successful execution of each WG depends on microarchitectural state that is not generally obvious to a developer. We created a framework, essentially a WC compiler, for building WCs we call skelly that abstracts away the the state of the microarchitecture. This framework is a static library that provides basic logic functions in c such as int and(int a, int b); and automatically takes care of such considerations as intentional i-cache misalignment and optimization of number and position of NOP sleds needed for gate stability. skelly also offers optional redundancy features which we used in our SHA-1 implementation. We used this framework to evaluate all WGs and WCs mentioned in this paper. For evaluation we enabled architecturally visible output in the form of load times in CPU cycles on output data cache based WRs. The load times map to logic values such that load times less than about (depending on gate) 100 cycles indicate a logic 1 and more than 100 cycles indicate a logic 0. This is because a short load time indicates something is in cache which we defined to be logic 1 as described earlier in this article. The experimental results for our TSX WGs are the result of 64 000 executions per gate with random gate input. We found these gates to have high accuracy which is shown in Table 3. Table 4 shows some statistics on how many CPU cycles are required to load the output WR from the TSX XOR gate. As expected when the inputs are and the load times are CPU cycles and when the inputs are and the load times are . Figure 4 shows the Kernel Density Estimations (KDEs) of the load times for TSX-AND. A KDE is similar to a smoothed histogram charting probability that it will take a given number of cycles to load the output WR. Probabilities well separated by a threshold value provide a visualization of gate stability. KDEs from 4 experiments of the same type are plotted on the same axis showing similar distributions between experiment runs. In evaluating the branch predictor / instruction cache based AND & OR we performed 320 000 operations per gate type using random input. These WGs are extremly accurate as shown in Table 5.
| Gate | Correct Ops | TSX Aborts | Total Ops | Mean Accuracy |
|---|---|---|---|---|
| AND | 62880 | 7 | 64000 | 0.98 |
| OR | 61922 | 9 | 64000 | 0.97 |
| AND-OR | 61152 | 12 | 64000 | 0.98 |
| XOR | 59259 | 8 | 64000 | 0.93 |
TSX-XOR Output WR Load Time (CPU cycles).| Input | Min | Q1 | Med | Q3 | Max | Std Dev | Mean |
|---|---|---|---|---|---|---|---|
| 0,0 | 31 | 220 | 222 | 228 | 20323 | 963.35 | 432.87 |
| 0,1 | 31 | 34 | 36 | 37 | 15656 | 360.44 | 75.40 |
| 1,0 | 31 | 34 | 36 | 37 | 16525 | 344.31 | 71.67 |
| 1,1 | 31 | 212 | 222 | 226 | 19200 | 883.15 | 382.07 |
| Gate | Operations | Correct | Mean Accuracy |
|---|---|---|---|
| AND | 320000 | 319994 | 0.999982 |
| OR | 320000 | 319988 | 0.999963 |
7. Conclusion
We have introduced the concept of WMs: a methodology for harnessing the computing capability provided via the unspecified aspects of CPU microarchitectures. We have described a framework for programmatically storing and operating on MA state as WRs and WGs respectively using several MA components. We demonstrated the practicallity of WMs by creating a microarchitecture-sensitive logic bomb as well as the implementation of a reasonably complex cryptographic algorithm, SHA-1. We believe that our work merely uncovers the tip of the iceberg: we believe that WMs will have strong applications in both offensive and defensive adversarial scenarios in the future.





Join the Discussion (0)
Become a Member or Sign In to Post a Comment