For many years, traditional signal processing has relied on the Shannon-Nyquist theory, which states that the number of samples required to capture a signal must be determined by the signal’s bandwidth. An alternative sampling theory, called compressed sensing or compressive sampling, turns the Shannon-Nyquist theory on its head. The idea behind compressed sensing is to accurately acquire signals from relatively few samples. The theory was so revolutionary when it was created a few years ago that an early paper outlining it was initially rejected on the basis that its claims appeared impossible to substantiate.
Today, however, compressed sensing is attracting a great deal of interest from mathematicians, computer scientists, and both optical and electrical engineers. And the theory is inspiring a new wave of lab work to produce systems that require far less power and operate more efficiently than those that rely on the traditional capture-compress paradigm. These systems include applications for industrial imaging, digital photography, biomedical imaging, and other forms of analog-to-digital conversion.
Compressed sensing emerged initially from an experiment inspired by a real-world problem with magnetic resonance imaging (MRI). The goal of the experiment, headed by Charles Mistretta at the University of Wisconsin, Madison, was to speed up the notoriously slow MRI process to make it more comfortable for patients, compensate for their minor movements, increase MRI throughput, and possibly even make the process fast enough to conduct 3D imaging. Because MRI hardware relies on a quantum effect to determine the density of protons in a patient’s body, the data-capture process cannot be shortened by improving the hardware’s core technology. Therefore, the question initially posed by the researchers working on the problem is whether the time it takes to perform an MRI can be reduced by capturing fewer samples and reconstructing a full image from only a small fraction of the traditional amount of required data. While conventional sampling theory suggests doing so would not be possible, the University of Wisconsin researchers applied standard image-reconstruction algorithms on heavily subsampled MRI data. But the results were inadequate, so the researchers turned to Emmanuel Candes, a professor of applied and computational mathematics at the California Institute of Technology, for assistance. Candes and his Caltech team set out to reconstruct the MRI images without any artifacts and by using only 5% of the sampled imaging data.
“When I looked at the artifacts, I discovered that they had certain features that I knew I could make go away by penalizing them in the reconstruction,” says Candes, who notes he was simply hoping his algorithm would improve the quality of the images. “That’s where the surprise came in,” he says. “What I was not expecting was that it would give me the truth.” Candes says that he and his team quickly realized they could do something that nobody thought was possible: simultaneous acquisition and compression. “That was the birth of compressed sensing,” he says. “We found that you can reconstruct images from dramatically fewer samples than what was previously necessary.”
Justin Romberg, who worked with Candes on the initial MRI project, points out that finding sparse signals that satisfy a set of linear constraints was an idea “floating around in the literature” at the time. However, he says, no existing theories supported the notion that it would be possible to perform reconstruction from limited data. “We were the first people to talk about it in this way,” says Romberg, a professor of electrical and computer engineering at the Georgia Institute of Technology. Of course, compressed sensing does not make it possible to reconstruct anything and everything from limited information. The target image or data set must have some special structure. “If there is structure, you can actually do much better than the Shannon-Nyquist theorem dictates,” says Romberg. “You can sample more efficiently.”
There are many projects in research labs around the world to build hardware that can leverage some of the core ideas associated with compressed sensing, so one might assume that the theory has come of age. But given the requirement to know some structure of the expected signal prior to sampling—implying that a random signal or one consisting entirely of noise would not be well suited to compressed sensing—the research team sought to establish firm mathematical foundations for their results. “For the theory, we know a lot today, not all that we would like to know,” says Candes. “But in broad strokes, the foundation is there.”
Theoretical Applications
One of the people who helped establish this foundation is Terence Tao, a professor of mathematics at the University of California, Los Angeles. “Emmanuel had found a toy problem in pure mathematics which, if solved, could lead to a practical demonstration that compressed sensing could actually work effectively,” says Tao. “That problem was in two areas in my own expertise—Fourier analysis and random matrices—and so I started to play around with it.” Eventually, says Tao, he, Candes, and Romberg solved that toy problem, establishing that compressed sensing worked for a certain type of measurement related to the Fourier transform, and started working together to further develop the theory. “I would not say that the field is anywhere as mature as, say, Shannon’s theory of information, or the statistical theory of least squares regression, which are some of the precursors to this subject,” says Tao. “But the core ideas of the subject are by now quite well understood, even if there are still many areas where we would like to develop them further.”
Compressed sensing is leading to new ways of looking at math problems in seemingly unrelated areas.
One of the areas that needs more attention, according to Tao, is how the theory is centered around linear measurement. “We don’t yet know what to do if our measurement devices behave nonlinearly with respect to the data,” Tao says. “We are still exploring exactly what type of measurement models compressed sensing excels at, and where the paradigm reaches its limits and must be replaced or supplemented by a different type of method.”
Compressed sensing works for a large number of special-purpose situations, says Tao, but is probably not suitable as a general-purpose tool. For instance, he says, it is unlikely that general-purpose digital cameras will rely on compressed sensing, given that consumers might want to take pictures that look like random, unstructured images. “But a dedicated sensor network that is devoted to detecting a certain special type of signal might benefit substantially from this paradigm,” he says.
Indeed, compressed sensing is having an impact on the designs of a broad array of such applications, given that sensors can be found almost everywhere. Engineers at Rice University, for example, are working on a single-pixel camera that can take high-quality photos by using compressed sensing and a digital micromirror array. In addition, space agencies have shown interest in the theory, with initial designs outlined for cameras that rely on compressed sensing to save power in deep space. And Candes and Romberg are working on a project with DARPA to overcome some of the traditional limitations associated with the analog-to-digital conversion of radio signals. The project’s goal is to design a system for monitoring radio frequency bands much more efficiently than is currently possible. The first chip for the project, which will sample frequencies at a rate of 800 million data points per second, is in fabrication now, and should soon be ready for testing. “One application for this kind of system,” says Romberg, “would be for monitoring large swaths of communications bandwidth, where you don’t necessarily know which frequency would be used for communicating.”
Mathematical Insights
In addition to having an impact on the design of sensor systems and other industrial applications, compressed sensing is leading to new ways of looking at math problems in seemingly unrelated areas. Candes and Tao, for example, are currently working on the problem of matrix prediction, the most widely known example of which is the Netflix Prize. The goal of those working to win the prize is to improve the accuracy of the Netflix movie-recommendation system. Each Netflix customer watches and rates a small fraction of movies, so it is possible to know only a little of the matrix in advance. While other mathematical approaches, such as spectral graph theory, have been applied to such matrix-prediction problems, Candes and Tao say there are strong parallels to the kinds of problems that compressed sensing can address. “The point is that we believe the ratings matrix to be structured,” says Tao. “Emmanuel and I are not working directly on the Netflix Prize problem, but on some more foundational mathematical issues related to one approach to solving this problem.”
Compressed sensing has applications for biomedical imaging, digital photography, and other forms of analog-to-digital conversion.
As for the future of the theory, Romberg says that one challenge remaining for those working on compressed sensing is convincing people that there is some value in it, and a corresponding value in changing sensor systems that have been implemented in certain ways since the beginning of signal processing. “A lot of the theory of compressed sensing,” he says, “goes against everything that sensors have been designed to do.” Another challenge is developing more efficient reconstruction algorithms. Traditionally, the signal-processing workload happens during encoding (such as for music and image files), while the decoder does very little. In compressed sensing, the workload is reversed; the encoder does very little, but the decoder has to work to find the location of the signal, its amplitude, and other characteristics. “A question that is active and that must remain active is how to get very fast algorithms to do the reconstruction,” says Candes.
For his part, Tao says compressed sensing is here to stay. “Perhaps in five or l0 years most of the issues people are actively studying now will be resolved or their limitations understood much better,” he says. “There is certainly a lot of potential, particularly in specific fields such as MRI, in which there was a definite need to squeeze more information out of fewer measurements.”
But compressed sensing’s impact, Tao says, is likely to be uneven, given that traditional methods might be more effective for some applications due to the limitations of compressed sensing that aren’t completely understood.
According to Candes, at least one impact of the theory is happening outside the research labs and on a more organic, social level. Candes says that when he attends conferences related to compressed sensing, he regularly sees pure mathematicians, applied mathematicians, computer scientists, and hardware engineers coming together to share ideas about the theory and its applications. “It’s really exciting to see all these people talk together,” Candes says. “I know compressed sensing is changing the way people think about data acquisition.”
Figures
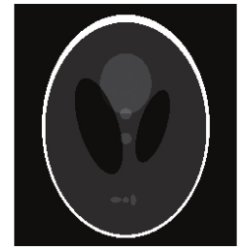
 Figure. The left MRI image suffers from blurred edges, numerous artifacts, and low resolution. The phantom image on the right was produced with minimally sampled Fourier coefficients using 5% of the original MRI data, and is the same as the original MRI phantom (not shown here).
Figure. The left MRI image suffers from blurred edges, numerous artifacts, and low resolution. The phantom image on the right was produced with minimally sampled Fourier coefficients using 5% of the original MRI data, and is the same as the original MRI phantom (not shown here).
 Figure. The left image represents high-frequency radar pulses. In the right image, the original signal (blue) is overlapped by the reconstructed signal (red), which was built through compressed sensing at a rate that is 6% of what is required by the Shannon-Nyquist theory.
Figure. The left image represents high-frequency radar pulses. In the right image, the original signal (blue) is overlapped by the reconstructed signal (red), which was built through compressed sensing at a rate that is 6% of what is required by the Shannon-Nyquist theory.



Join the Discussion (0)
Become a Member or Sign In to Post a Comment