­nique Games Conjecture Results in Nevanlinna Prize

The International Mathematical Union (IMU) this week awarded the prestigious Rolf Nevanlinna Prize to Subhash Khot, a professor in the Computer Science department at New York University’s Courant Institute of Mathematical Sciences, during at the International Congress of Mathematicians in Seoul, South Korea.

The award recognizes outstanding contributions in all mathematical aspects of computer science, as well as in scientific computing and numerical analysis. The prize is targeted at young mathematicians, who must be under 40 years of age on Jan. 1 of the year the award is given.

The IMU awarded Khot this year’s Nevanlinna Prize “for his prescient definition of the ‘Unique Games’ problem, and leading the effort to understand its complexity and its pivotal role in the study of efficient approximation of optimization problems.”

The organization noted that Khot’s work “led to breakthroughs in algorithmic design and approximation hardness, and to new exciting interactions between computational complexity, analysis and geometry,” adding that “the Unique Games Conjecture will be driving research in theoretical computer science for many years to come.”

Lance Fortnow, chair of the School of Computer Science at the Georgia Institute of Technology, says the IMU’s recognition of Khot could help draw more attention to these types of problems.  “People within the complexity field know of Khot’s work, but I think it generates more attention from mathematicians,” Fortnow says. Moreover, the award is only given out every four years, so its recipients constitute an exclusive class.

The Nevanlinna Prize has “become the most prestigious prize for theoretical computer science,” Fortnow says. “It has given at the same time and the same meeting as the Fields medal, which is the top prize for mathematicians.”

Khot ‘s award-winning work is based on his 2002 theorem known as Unique Games Conjecture (UGC), which asserts that the problem of determining the approximate value of a certain type of game, known as a unique game, has Non-deterministic Polynomial-time hard (NP-hard) algorithmic complexity.

So-called “NP-hard” problems are those which most computer scientists believe cannot be solved exactly by any algorithm that runs in a reasonable amount of time. An example of this type of problem would be arranging a seating plan for a wedding, where a set of constraints (such as feuding family members) would add to the complexity, due to the large number of possible solutions.

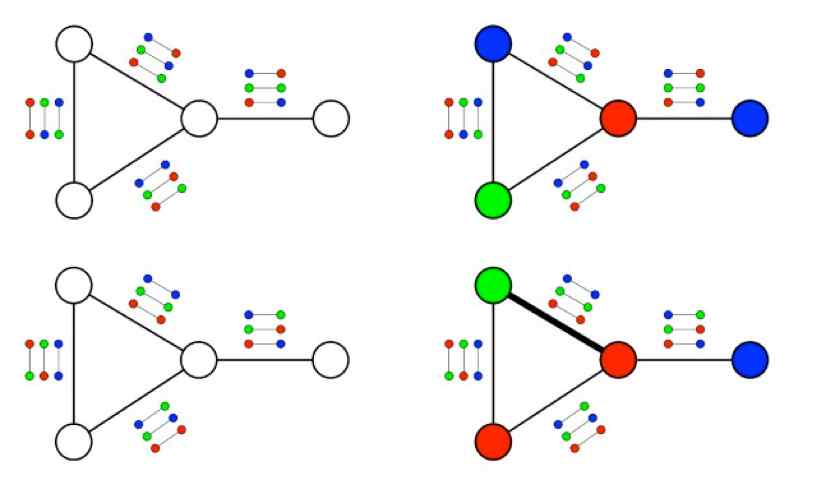
Khot’s Unique Games Conjecture addresses these types of NP-hard problems through the use of the Network Coloring problem, which considers a network of nodes and a set of colors, and asks whether it is possible to color the vertices of the network in such a way that two vertices that share an edge always have different colors.

In the case of only two colors, such as red and green in the diagram above, it is easy to answer this question efficiently for any given network, as the colors will simply alternate until the network has been colored completely or a contradiction arises. If more than two colors are in play, choosing the color of one vertex does not force the color of any of the vertices connected to it, deciding which nodes can be colored is an NP-hard problem.

Khot decided to address networks that come equipped with a set of coloring rules, or constraints, such that if two vertices are connected by an edge, then whenever one edge gets colored, a constraint specifies the color of the other edge. By initiating such constraints, an algorithm similar to the one for two colors could determine whether the network can be colored in a way that satisfies the constraints.

Khot’s UGC deals with the next natural question:  for a network that cannot be colored in a way that satisfies all constraints, which coloring satisfies the most constraints possible?

While Khot did not respond to requests for comment, a key issue that has been raised in the scientific community is that UGC remains unproven. However, its influence on other research areas has already been felt, according to Fortnow.

“The neat thing about the research is how well it ties in with so many other research directions that are going on,” explains Fortnow. “The closest connection is with semi-definite programming, which is a relatively new algorithmic technique to get a better handle on some of the hardest problems in computer science, which deals with approximate solutions. Unique Games Conjecture really seems to capture the hardness of this semi-definite programming technique, and shows us the limits of what we can do with SDTs (software development tools).”

Fortnow notes that UGC is also impacting, although to a significantly lesser degree, research in the areas of coding theory, quantum computing, and voting theory.

Keith Kirkpatrick is principal of 4K Research & Consulting, LLC, based in Lynbrook, NY.