Why Not Program Right?

Normal 0 false false false false EN-US X-NONE X-NONE Most of the world programs in a very strange way. Strange to me. I usually hear the reverse question: people ask us, the Eiffel community, to explain why we program our way. I hardly understand the question, because the only mystery is how anyone can even program in any other way.

The natural reference is the beginning of One Flew Over the Cuckoo’s Nest: when entering an insane asylum and wondering who is an inmate and who a doctor, you may feel at a loss for objective criteria. Maybe the rest of the world is right and we are the nut cases. Common sense suggests it.

But sometimes one can go beyond common sense and examine the evidence. So lend me an ear while I explain my latest class invariant. Here it is, in Figure 1. (Wait, do not just run away yet.)

Figure 1: The invariant of class MULTIGRAPH

This is a program in progress and by the time you read this note the invariant and enclosing class will have changed. But the ideas will remain.

Context: multigraphs

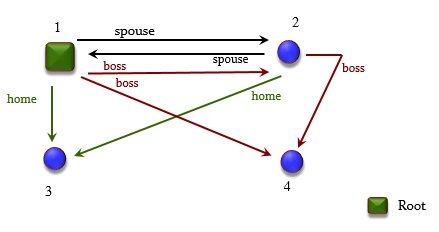
The class is called MULTIGRAPH and describes a generalized notion of graph, illustrated in Figure 2. The differences are that: there can be more than one edge between two nodes, as long as they have different tags (like the spouse and boss edges between 1 and 2); and there can be more than one edge coming out of a given node and with a given tag (such as the two boss edges out of 1, reflecting that 1’s boss might be 2 in some cases and 3 in others). Some of the nodes, just 1 here, are “roots”.

The class implements the notion of multigraph and provides a wide range of operations on multigraphs.

Figure 2: A multigraph

Data structures

Now we turn to the programming and software engineering aspects. I am playing with various ways of accessing multigraphs. For the basic representation of a multigraph, I have chosen a table of triples:

                triples_table: HASH_TABLE [TRIPLE, TUPLE [source: INTEGER; tag: INTEGER; target: INTEGER]]                                    — Table of triples, each retrievable through its `source’, `tag’ and `target’.

where the class TRIPLE describes [source, tag, target] triples, with a few other properties, so they are not just “tuples”. It is convenient to use a hash table, where the key is such a 3-tuple. (In an earlier version I used just an ARRAY [TRIPLE], but a hash table proved more flexible.)

Sources and targets are nodes, also called “objects”; we represent both objects and tags by integers for efficiency. It is easy to have structures that map symbolic tag names such as “boss” to integers.

triples_table is the core data structure but it turns out that for the many needed operations it is convenient to have others. This technique is standard: for efficiency, provide different structures to access and manipulate the same underlying information, with some redundancy. So I also have:

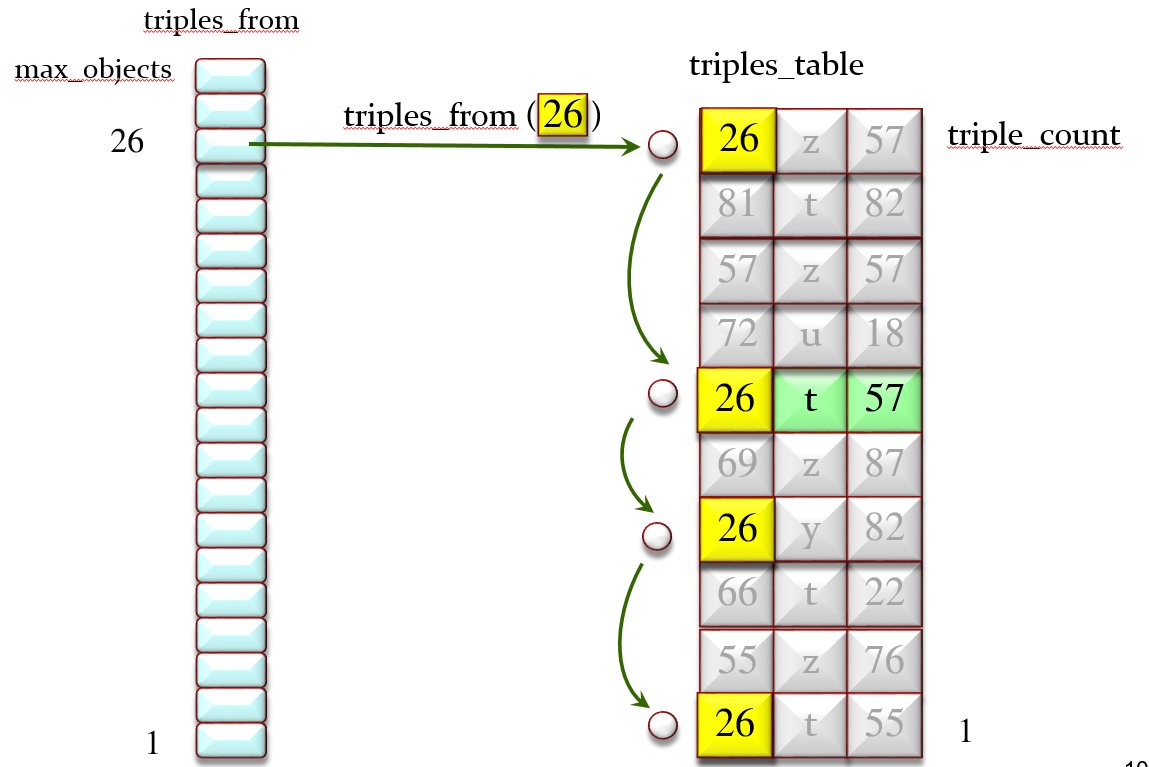
 triples_from:  ARRAYED_LIST [LIST [TRIPLE]]
               — Triples starting from a given object. Indexed by object numbers.

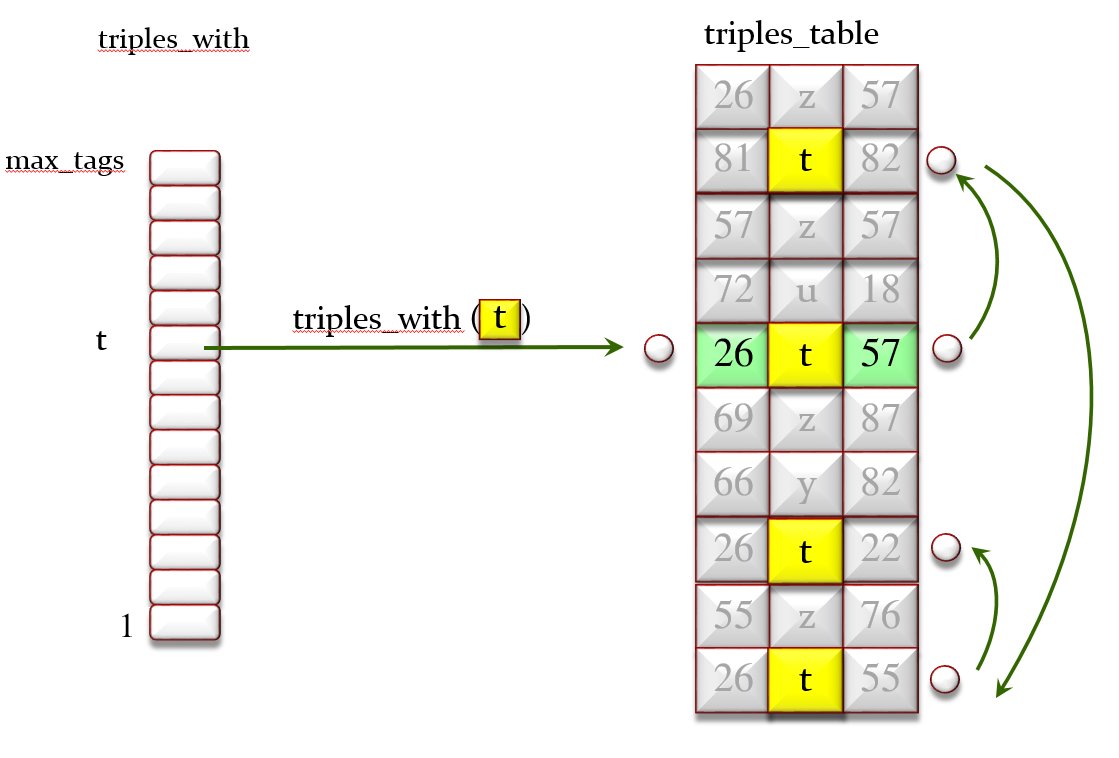
  triples_with:  HASH_TABLE [LIST [TRIPLE], INTEGER]
               — Triples labeled by a given tag. Key is tag number.

 triples_to:  ARRAYED_LIST [LIST [TRIPLE]]
               — Triples leading into a given object. Indexed by object numbers.

Figure 3 illustrates triples_from and Figures 4 illustrates triples_with. triples_to is similar.

Figure 3: The triples_from array of lists and the triples_table

 

 

Figure 4: The triples_with array of lists and the triples_table

It is also useful to access multigraphs through yet another structure, which gives us the targets associated with a given object and tag:

 

successors: ARRAY [HASH_TABLE [LIST [TRIPLE], INTEGER]]
               — successors [obj] [t] includes all o such that there is a t- reference from obj to o.

 

For example in Figure 1 successors [1] [spouse] is {2, 3}, and in Figures 3 and 4 successors [26] [t] is {22, 55, 57}. Of course we can obtain the “successors” information through the previously defined structures, but since this is a frequently needed operation I decided to include a specific data structure (implying that every operation modifying the multigraph must update it). I can change my mind later on and decide to make “successors” a function rather than a data structure; it is part of the beauty of OO programming, particularly in Eiffel, that such changes are smooth and hardly impact client classes.

There is similar redundancy in representing roots:

                roots:  LINKED_SET [INTEGER]
                              — Objects that are roots.

                is_root:  ARRAY [BOOLEAN]
                              — Which objects are roots? Indexed by object numbers.

 

If o is a root, then it appears in the “roots” set and is_root [o] has value True.

Getting things right

These are my data structures. Providing such a variety of access modes is a common programming technique. From a software engineering perspective ― specification, implementation, verification… ― it courts disaster. How do we maintain their consistency? It is very easy for a small mistake to slip into an operation modifying the graph, causing one of the data structures to be improperly updated, but in a subtle and rare enough way that it will not manifest itself during testing, coming back later to cause strange behavior that will be very hard to debug.

For example, one of the reasons I have a class TRIPLE and not just 3-tuples is that a triple is not exactly  the same as an edge in the multigraph. I have decided that by default the operation that removes and edge would not remove the corresponding triple from the data structure, but leave it in and mark it as “inoperative” (so class TRIPLE has an extra “is_inoperative” boolean field). There is an explicit GC-like mechanism to clean up deleted edges occasionally. This approach brings efficiency but makes the setup more delicate since we have to be extremely careful about what a triple means and what removal means.

This is where I stop understanding how the rest of the world can work at all. Without some rigorous tools I just do not see how one can get such things right. Well, sure, spend weeks of trying out test cases, printing out the structures, manually check everything (in the testing world this is known as writing lots of “oracles”), try at great pains to find out the reason for wrong results, guess what program change will fix the problem, and start again. Stop when things look OK. When, as Tony Hoare once wrote, there are no obvious errors left.

Setting aside the minuscule share of projects (typically in embedded life-critical systems) that use some kind of formal verification, this process is what everyone practices. One can only marvel that systems, including many successful ones, get produced at all. To take an analogy from another discipline, this does not compare to working like an electrical engineer. It amounts to working like an electrician.

For a short time I programmed like that too (one has to start somewhere, and programming methodology was not taught back then). I no longer could today. Continuing with the Hoare citation, the only acceptable situation is to stop when there are obviously no errors left.

How? Certainly not, in my case, by always being right the first time. I make mistakes like everyone else does. But I have the methodology and tools to avoid some, and, for those that do slip through, to spot and fix them quickly.

Help is available

First, the type system. Lots of inconsistencies, some small and some huge, which in an untyped language would only hit during execution, do not make it past compilation. We are not just talking here about using REAL instead of INTEGER. With a sophisticated type system involving multiple inheritance, genericity, information hiding and void safety, a compiler error message can reflect a tricky logical mistake. You are using a SET as if it were a LIST (some operations are common, but others not). You are calling an operation on a reference that may be void (null) at run time. And so on.

By the way, about void-safety: for a decade now, Eiffel has been void-safe, meaning a compile-time guarantee of no run-time null pointer dereferencing. It is beyond my understanding how the rest of the world can still live with programs that run under myriad swords of Damocles: x.op (…) calls that might any minute, without any warning or precedent, hit a null x and crash.

Then there is the guarantee of logical consistency, which is where my class invariant (Figure 1) comes in. Maybe it scared you, but in reality it is all simple concepts, intended to make sure that you know what you are doing, and rely on tools to check that you are right. When you are writing your program, you are positing all kinds, logical assumptions, large and (mostly) small, all the time. Here, for the structure triples_from [o] to make sense, it must be a list such that:

• It contains all the triples t in the triples_table such that t.source = o.
•  It contains only those triples!

You know this when you write the program; otherwise you would not be having a “triples_from” structure. Such gems of knowledge should remain an integral part of the program. Individually they may not be rocket science, but accumulated over the lifetime of a class design, a subsystem design or a system design they collect all the intelligence that makes the software possible.  Yet in the standard process they are gone the next minute! (At best, some programmers may write a comment, but that does not happen very often, and a comment has no guarantee of precision and no effect on testing or correctness.)

Anyone who takes software development seriously must record such fundamental properties. Here we need the following invariant clause:

across triples_from as tf all

across tf.item as tp all tp.item.source = tf.cursor_index end

end

(It comes in the class, as shown in Figure 1, with the label “from_list_consistent”. Such labels are important for documentation and debugging purposes. We omit them here for brevity.)

What does that mean? If we could use Unicode (more precisely, if we could type it easily with our keyboards) we would write things like “ x: E | P (x) for all x in E, property P holds of x. We need programming-language syntax and write this as across E as x all P (x.item) end. The only subtlety is the “.item” part, which gives us generality beyond the “ notation: x in the across is not an individual element of E but a cursor that moves over E. The actual element at cursor position is x.item, one of the properties of that cursor. The advantage is that the cursor has more properties, for example x.cursor_index, which gives its position in E. You do not get that with the plain “ of mathematics.

If instead of “ you want $ (there exists), use some instead of all. That is pretty much all you need to know to understand all the invariant clauses of class MULTIGRAPH as given in Figure 1.

So what the above invariant clause says is: take every position tf in triples_from; its position is tf.cursor_index and its value is tf.item. triples_from is declared as ARRAYED_LIST [LIST [TRIPLE]], so tf.cursor_index is an integer representing an object o, and tf.item is a list of triples. That list should  consist of the triples having tf.cursor_index as their source. This is the very property that we are expressing in this invariant clause, where the innermost across says: for every triple tp.item in the list, the source of that triple is the cursor index (of the outside across). Simple and straightforward, I think (although such English explanations are so much more verbose than formal versions, such as the Eiffel one here, and once you get the hang of it you will not need them any more).

How can one ever include a structure such as triples_from without expressing such a property? To put the question slightly differently: am I inside the asylum looking out, or outside the asylum looking in? Any clue would be greatly appreciated.

More properties

For the tag (“with_“) and target lists, the properties are similar:

across triples_with as tw all across tw.item as tp all tp.item.tag = tw.key end end

across triples_to as tt all across tt.item as tp all tp.item.target = tt.cursor_index end end 

We also have some properties of array bounds:

 is_root.lower = 1 and is_root.upper = object_count

triples_from.lower = 1 and triples_from.upper = object_count

triples_to.lower = 1 and triples_to.upper = object_count

where object_count is the number of objects (nodes), and for an array a (whose bounds in Eiffel are arbitrary, not necessarily 0 or 1, and set on array creation), a.lower and a.upper are the bounds. Here we number the arrays from 1.

There are, as noted, two ways to represent rootness. We must express their consistency (or risk trouble). Two clauses of the invariant do the job:

across roots as t all is_root [t.item] end

across is_root as t all (t.item = roots.has (t.cursor_index)) end

The first one says that if we go through the list “roots” we only find elements whose “is_root” value is true; the second, that if we go through the array “is_root” we find values that are true where and only where the corresponding object, given by the cursor index, is in the “roots” set. Note that the “=” in that second property is between boolean values (if in doubt, check the type instantly in the EIffelStudio IDE!), so it means “if and only if”.

Instead of these clauses, a more concise version, covering them both, is just

roots ~ domain (is_root)

with a function domain that gives the domain of a function represented by a boolean array. The ~ operator denotes object equality, redefined in many classes, and in particular in the SET classes (“roots” is a LINKED_SET) to cover equality between sets, i.e. the property of having the same elements.

The other clauses are all similarly self-explanatory. Let us just go through the most elaborate one, successors_consistent, involving three levels of across:

across successors as httpl all                   — httpl.item: hash table of list of triples

        across httpl.item as tpl all                — tpl.item: list of triples (tpl.key: key (i.e. tag) in hash table (tag)

                  across tpl.item as tp all            — tp.item: triple

                         tp.item.tag = tpl.key

and tp.item.source = httpl.cursor_index

                   end

          end

end

You can see that I struggled a bit with this one and made provisions for not having to struggle again when I would look at the code again 10 minutes, 10 days or 10 months later. I chose (possibly strange but consistent) names such as httpl for hash-table triple, and wrote comments (I do not usually need any in invariant and other contract clauses) to remind me of the type of everything. That was not strictly needed since once again the IDE gives me the types, but it does not cost much and could help.

What this says: go over “successors“; which as you remember is an ARRAY, indexed by objects, of HASH_TABLE, where each entry of such a hash table has an element of type [LIST [TRIPLE] and a key of type INTEGER, representing the tag of a number of outgoing edges from the given object. Go over each hash table httpl. Go over the associated list of triples tpl. Then for each triple tp in this list: the tag of the triple must be the key in the hash table entry (remember, the key does denote a tag); and the source of the triple must the object under consideration, which is the current iteration index in the array of the outermost iteration.

I hope I am not scaring you at this point. Although the concepts are simple, this invariant is more sophisticated than most of those we typically write. Many invariant clauses (and preconditions, and postconditions) are very simple properties, such as x > 0 or x ≠ y. The reason this one is more elaborate is not that I am trying to be fussy but that without it I would be the one scared to death. What is elaborate here is the data structure and programming technique. Not rocket science, not anything beyond programmers typically do, but elaborate. The only way to get it right is to buttress it by the appropriate logical properties. As noted, these properties are there anyway, in the back of your head, when you write the program. If you want to be more like an electrical engineer than an electrician, you have to write them down.

There is more to contracts

Invariants are not the only kind of such “contract” properties. Here for example, from the same class, is a (slightly abbreviated) part of the postcondition (output property) of the operation that tells us, through a boolean Result, if the multigraph has an edge of given components osource, t (the tag) and otarget :

Result =

(across successors [osource] [t] as tp some

not tp.item.is_inoperative and tp.item.target = otarget

end)

In words, this clause expresses the compatibility of the operation with the “successors” view: it must answer yes if and only if otarget appears in the successor set of osource for t, and the corresponding triple is not marked inoperative.

The concrete benefits

And so? What do we get out of making these logical properties explicit? Just the intellectual satisfaction of doing things right, and the methodological guidance? No! Once you have done this work, it is all downhill. Turn on the run-time assertion monitoring option (tunable separately for preconditions, postconditions, invariants etc., and on by default in development mode), and watch your tests run. If you are like almost all of us, you will have made a few mistakes, some which will seem silly when or rather if you find them in time (but there is nothing funny about a program that crashes during operation) and some more subtle. Sit back, and just watch your contracts be violated. For example if I change “<=” to “<” in the invariant property “tw.key <= max_tag“, I get the result of Figure 5. I see the call stack that I can traverse, the object run-time structure that I can explore, and all the tools of a modern debugger for an OO language. Finding and correcting the logical flaw will be a breeze.

Figure 5: An invariant violation brings up the debugger

The difference

It will not be a surprise that I did not get all the data structures and algorithms of the class MULTIGRAPH  right the first time. The Design by Contract approach (the discipline of systematically expressing, whenever you write any software element, the associated logical properties) does lead to fewer mistakes, but everyone occasionally messes up. Everyone also looks at initial results to spot and correct mistakes. So what is the difference?

Without the techniques described here, you execute your software and patiently examine the results. In the example, you might output the content of the data structures, e.g.

List of outgoing references for every object:

        1: 1-1->1|D, 1-1->2|D, 1-1->3|D, 1-2->1|D, 1-2->2|D,  1-25->8|D, 1-7->1|D, 1-7->6|D,

1-10->8|D, 1-3->1|D, 1-3->2|D, 1-6->3|D, 1-6->4|D, 1-6->5|D

        3: 3-6->3, 3-6->4, 3-6->5, 3-9->14, 3-9->15,   3-9->16, 3-1->3, 3-1->2, 3-2->3, 3-2->2,

                  3-25->8, 3-7->3, 3-7->6, 3-10->8, 3-3->3,  3-3->2    

List of outgoing references for every object:

        1: 1-1->1|D, 1-1->2|D, 1-1->3|D, 1-2->1|D, 1-2->2|D, 1-25->8|D, 1-7->1|D, 1-7->6|D,

1-10->8|D, 1-3->1|D,  1-3->2|D, 1-6->3|D, 1-6->4|D, 1-6->5|D

        3: 3-6->3, 3-6->4, 3-6->5, 3-9->14, 3-9->15,  3-9->16, 3-1->3, 3-1->2, 3-2->3, 3-2->2,

                                 3-25->8, 3-7->3, 3-7->6, 3-10->8, 3-3->3,  3-3->2

and so on for all the structures. You check the entries one by one to ascertain that they are as expected. The process nowadays has some automated support, with tools such as JUnit, but it is still essentially manual, tedious and partly haphazard: you write individual test oracles for every relevant case. (For a more automated approach to testing, taking advantage of contracts, see [1].) Like the logical properties appearing in contracts, these oracles are called “assertions” but the level of abstraction is radically different: an oracle describes the desired result of one test, where a class invariant, or routine precondition, or postcondition expresses the properties desired of all executions.

Compared to the cost of writing up such contract properties (simply a matter of formalizing what you are thinking anyway when you write the code), their effect on testing is spectacular. Particularly when you take advantage of “across” iterator mechanisms. In the example, think of all the checks and crosschecks automatically happening across all the data structures, including the nested structures as in the 3-level across clause. Even with a small test suite, you immediately get, almost for free, hundreds or thousands of such consistency checks, each decreasing the likelihood that a logical flaw will survive this ruthless process.

Herein lies the key advantage. Not that you will magically stop making mistakes; but that the result of such mistakes, in the form of contract violations, directly points to logical properties, at the level of your thinking about the program. A wrong entry in an output, whether you detect it visually or through a Junit clause, is a symptom, which may be far from the cause. (Remember Dijkstra’s comment, the real point of his famous Goto paper, about the core difficulty of programming being to bridge the gap between the static program text, which is all that we control, and its effect: the myriad possible dynamic executions.) Since the cause of a bug is always a logical mistake, with a contract violation, which expresses a logical inconsistency, you are much close to that cause.

(About those logical mistakes: since a contract violation reflects a discrepancy between intent, expressed by the contract, and reality, expressed by the code, the mistake may be on either side. And yes, sometimes it is the contract that is wrong while the implementation in fact did what is informally expected. There is partial empirical knowledge [1] of how often this is the case. Even then, however, you have learned something. What good is a piece of code of which you are not able to say correctly what it is trying to do?)

The experience of Eiffel programmers reflects these observations. You catch the mistakes through contract violations; much of the time, you find and correct the problem easily. When you do get to producing actual test output (which everyone still does, of course), often it is correct.

This is what has happened to me so far in the development of the example. I had mistakes, but converging to a correct version was a straightforward process of examining violations of invariant violations and other contract elements, and fixing the underlying logical problem each time.

By the way, I believe I do have a correct version (in the sense of the second part of the Hoare quote), on the basis not of gut feeling or wishful thinking but of solid evidence. As already noted it is hard to imagine, if the code contains any inconsistencies, a test suite surviving all the checks.

Tests and proofs

Solid evidence, not perfect; hard to imagine, not impossible. Tests remain only tests; they cannot exercise all cases. The only way to achieve demonstrable correctness is to rely on mathematical proofs performed mechanically. We have this too, with the AutoProof proof system for Eiffel, developed in recent years [1]. I cannot overstate my enthusiasm for this work (look up the Web-based demo), its results (automated proof of correctness of a full-fledged data structures and algorithms library [2]) and its potential, but it is still a research effort. The dynamic approach (meaning test-based rather than proof-based) presented above is production technology, perfected over several decades and used daily for large-scale mission-critical applications. Indeed (I know you may be wondering) it scales up without difficulty:

• The approach is progressive. Unlike fully formal methods (and proofs), it does not require you to write down every single property down to the last quantifier. You can start with simple stuff like x > 0. The more you write, the more you get, but it is the opposite of an all-or-nothing approach.
• On the practical side, if you are wondering about the consequences on performance of a delivered system: there is none. Run-time contract monitoring is a compilation option, tunable for different kinds of contracts (invariants, postconditions etc.) and different parts of a system. People use it, as discussed here, for development, testing and debugging. Most of the time, when you deliver a debugged system, you turn it off.
• It is easy to teach. As a colleague once mentioned, if you can write an if-then-else you can write a precondition. Our invariants in the above example where a bit more sophisticated, but programmers do write loops (in fact, the Eiffel loop for iterating over a structure also uses across, with “loop” and instructions instead of “all” or “some” and boolean expressions). If you can write a loop over an array, you can write a property of the array’s elements.
• A big system is an accumulation of small things. In a blog article [5] I recounted how I lost a full day of producing a series of technical diagrams of increasing complexity, using one of the major Web-based collaborative development tools. A bug of the system caused all the diagrams to reproduce the first, trivial one. I managed to get through to the developers. My impression (no more than an educated guess resulting from this interaction) is that the data structures involved were far simpler than the ones used in the above discussion. One can surmise that even simple invariants would have uncovered the bug during testing rather than after deployment.
• Talking about deployment and tools used directly on the cloud: the action in software engineering today is in DevOps, a rapid develop-deploy loop scheme. This is where my perplexity becomes utter cluelessness. How can anyone even consider venturing into that kind of exciting but unforgiving development model without the fundamental conceptual tools outlined above?

We are back then to the core question. These techniques are simple, demonstrably useful, practical, validated by years of use, explained in professional books (e.g. [6]), introductory programming textbooks (e.g. [7]), EdX MOOCs (e.g. [8]), YouTube videos, online tutorials at eiffel.org, and hundreds of articles cited thousands of times. On the other hand, most people reading this article are not using Eiffel. On reflection, a simple quantitative criterion does exist to identify the inmates: there are far more people outside the asylum than inside. So the evidence is incontrovertible.

What, then, is wrong with me?

 

References

(Nurse to psychiatrist: these are largely self-references. Add “narcissism” to list of patient’s symptoms.)

1.    Ilinca Ciupa, Andreas Leitner, Bertrand Meyer, Manuel Oriol, Yu Pei, Yi Wei and others: AutoTest articles and other material on the AutoTest page.

2. Bertrand Meyer, Ilinca Ciupa, Lisa (Ling) Liu, Manuel Oriol, Andreas Leitner and Raluca Borca-Muresan: Systematic evaluation of test failure results, in Workshop on Reliability Analysis of System Failure Data (RAF 2007), Cambridge (UK), 1-2 March 2007 available here.

3.    Nadia Polikarpova, Ilinca Ciupa and Bertrand Meyer: A Comparative Study of Programmer-Written and Automatically Inferred Contracts, in ISSTA 2009: International Symposium on Software Testing and Analysis, Chicago, July 2009, available here.

4.    Carlo Furia, Bertrand Meyer, Nadia Polikarpova, Julian Tschannen and others: AutoProof articles and other material on the AutoProof page. See also interactive web-based online tutorial here.

5.    Bertrand Meyer, The Cloud and Its Risks, blog article, October 2010, available here.

6.    Bertrand Meyer, Object-Oriented Software Construction, 2^nd edition, Prentice Hall, 1997.

7.    Bertrand Meyer, Touch of Class: Learning to Program Well Using Objects and Contracts, Springer, 2009, see touch.ethz.ch and Amazon page.

8.    MOOCs (online courses) on EdX : “Computer: Art, Magic, Science”, Part 1 and Part 2. (Go to “archived versions” to follow the courses.)