
Concurrent message passing was crucially omitted from the lambda calculus [Church 1932], Turing Machines (TM) [Turing 1936], Simula-67 [Dahl and Nygaard 1967], and Logic Programs [Hewitt 1969], thereby crippling them as a foundation for the Internet of Things (IoT). Actors [Hewitt, et. al 1973] remedied the omission to provide for scalable computation. An Actor message passing machine can be millions of times faster than any corresponding pure Logic Program or parallel nondeterministic lambda expression. Since the time of this early work, message passing has grown to be one of the most important paradigms in computing [Hewitt and Woods 2018; Hoare 2016; Milner 1993].
Of course, earlier work made huge pioneering contributions: lambda expressions play an important role in programming languages. TM inspired development of the stored program sequential computer. Simula-67 became the basis for object-oriented programming in Java and C++. Logic Programs are fundamental to Scalable Intelligent Systems. [Hewitt and Woods 2018]
Message Passing in Practice
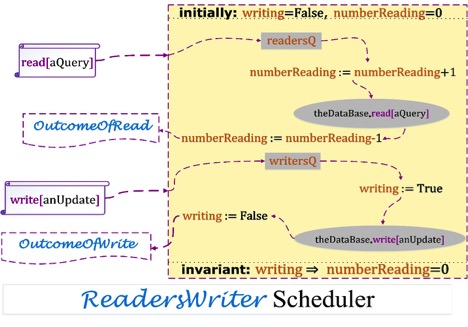
Concurrency control for readers and writers in a database is a classic problem that illustrates the power of message passing. The fundamental constraint is that multiple writers are not allowed to operate concurrently in the database and a writer is not allowed to operate concurrently with a reader. In the figure below for an Actor machine
- Yellow is used for the Actor’s region of mutual exclusion
- Within the region of mutual exclusion, a hole in grey allows other messages to be processed which are of two kinds:
- Queue (shown as rectangle) hole in which the current activity can be suspended until resumed
- Call-out (shown as oval) hole for a request made outside the region of mutual exclusion
Many different policies could be implemented in the above scheduler including the following:
- Reader priority: When a writer comes out of the database, resume all in ReadersQ.
- Writer priority: When a writer comes out of the database and both WritersQ and ReadersQ are nonempty, resume just one in ReadersQ, and then when it comes of the database resume one in WritersQ.
Computation that cannot be done by lambda Calculus, TM, or pure Logic Programs
Actor message passing machines can perform computations that a no lambda expression, nondeterministic Turing Machine, Simula-67 program, or pure Logic Program can implement. Below is an example of a very simple computation that cannot be performed by a nondeterministic TM:
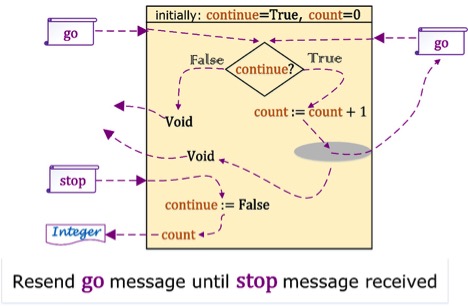
There is an always-halting Actor message passing machine that can compute an integer of unbounded size. This is accomplished using variables count initially 0 and continue initially True. The computation is begun by concurrently sending over the Internet two messages to the Actor machine: a stop request that will return an integer n formalized as Output[n] and a go message that will return Void.
The Actor machine operates as follows:
- When a go message is received:
- If continue is True, increment count by 1, send this Actor machine a go message in a hole of the region of mutual exclusion, and afterward return Void.
- If continue is False, return Void.
- When a stop message is received, return count and set continue to False for the next message received.
Theorem. There is no lambda expression, nondeterministic Turing Machine, Simula-67 program, or pure Logic Program that implements the above computation.
Proof [Plotkin 1976]:
“Now the set of initial segments of execution sequences of a given nondeterministic program P, starting from a given state, will form a tree. The branching points will correspond to the choice points in the program. Since there are always only finitely many alternatives at each choice point, the branching factor of the tree is always finite. That is, the tree is finitary. Now König’s lemma says that if every branch of a finitary tree is finite, then so is the tree itself. In the present case this means that if every execution sequence of P terminates, then there are only finitely many execution sequences. So if an output set of P is infinite, it must contain a nonterminating computation.”
Limitations of 1st Order Logic for Concurrent Computation
Theorem. It is well known that there is no 1st order theory for the above Actor machine.
Proof. Every 1st order theory is compact meaning that every inconsistent set of propositions has a finite inconsistent subset. Consequently, to show that there is no 1st order theory, it is sufficient to show that there is an inconsistent set of propositions such that every finite subset is consistent. The set of propositions NoOutput defined to be {~Output[i] | i:N} is inconsistent meaning |-~NoOutput (because ⊢∃[i:N] Output[i], i.e., the Actor machine always outputs an integer) but every finite subset S of NoOutput is consistent meaning ~|-~S (because by finiteness of S, there is an upper bound b:N such that S is a subset of {~Output[i] | i<b} but ~|-~{~Output[i] | i<b} and therefore S is consistent because ~|- ~S, i.e., the Actor machine output might be larger than b).
Parting thoughts
Message passing has fundamentally transformed the foundations and practice of computation since the initial conceptions of Turing and Church. Although 1st order sentences can be useful (e.g. in SAT solvers), message passing illustrates why 1st order logic cannot be the foundation for theories in Computer Science.
References
Alonzo Church. A set of postulates for the foundation of logic Annals of Mathematics. Series 2. 33 (2). 1932.
Ole-Johan Dahl and Kristen Nygaard. Class and subclass declarations IFIP TC2 Conference on Simulation Programming Languages. May 1967.
Carl Hewitt. Planner: A Language for Proving Theorems in Robots IJCAI-69.
Carl Hewitt, Peter Bishop and Richard Steiger. A Universal Modular Actor Formalism for Artificial Intelligence IJCAI’73.
Carl Hewitt and John Woods assisted by Jane Spurr. Inconsistency Robustness, 2nd Edition Studies in Logic. 2018.
Tony Hoare. Discrete Geometric Representation of Concurrent Program Execution Heidelberg Laureate Forum. September 23, 2016.
Robin Milner Elements of interaction: Turing award lecture CACM. January 1993.
Gordon Plotkin. A powerdomain construction SIAM Journal of Computing. September 1976.
Alan Turing. On Computable Numbers, with an Application to the Entscheidungsproblem Proceedings of the London Mathematical Society. November 1936.
Carl Hewitt is an emeritus professor of the Massachusetts Institute of Technology. He is board chair of iRobust, an international scientific society for the promotion of the field of Inconsistency Robustness, and board chair of Standard IoT, an international standards organization for the Internet of Things, which is using the Actor Model to unify and generalize emerging standards for IoT.



Join the Discussion (0)
Become a Member or Sign In to Post a Comment