Calculating With Roman Numerals is Not So Difficult

We calculate in the decimal place-value system using Hindu-Arabic numerals. But how to deal with Roman numerals and without a sign for zero in an additive number system, if no hand abacus is available? (See also Communications of the ACM: How Did the Romans Calculate?).

Preliminary remarks

When calculating with Roman numerals, the order of the numerals is irrelevant. Exceptions: If a smaller unit is to the left of a larger unit, it is subtracted from the larger unit: IV, IX, IL, IC, ID, IM; VL, VC, VD, VM; XL, XC, XD, XM; LD, LM as well as CD and CM.

Addition

The augend and the addend are added in the same way as with the abacus (see Tab. 1–2). If necessary, the number symbols must be combined (bundled).

Tab. 1: Addition in the Roman number system 1

 

Tab. 2: Addition in the Roman number system 2

 

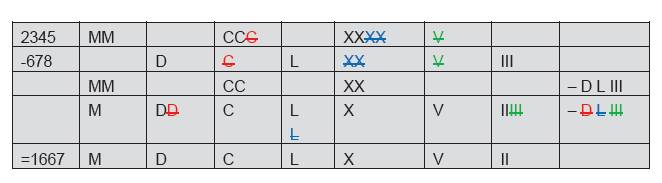
Subtraction

The subtrahend is subtracted from the minuend in a way similar to the abacus (see Table 3). If necessary, the numeral signs must be resolved (disassembled). Numbers that occur both in the minuend and in the subtrahend can be deleted.

 

Tab. 3: Subtraction in the Roman numerical system

 

Multiplication

Multiplication is a repeated addition. The multiplicand 23 is added 6 times (see Table 4). You calculate in the same way on the abacus, and most mechanical calculators use a similar procedure. In the Middle Ages there were also other methods, such as doubling (duplation), Gelosia method (lattice multiplication), and Egyptian multiplication (Ethiopian multiplication).

 

Tab. 4: Multiplication in the Roman number system

 

Division

Division is a successive subtraction. Divisor 7 can be deducted 8 times from dividend 56 (see Table 5). You calculate in the same way on the abacus, and most mechanical calculators use a similar procedure. In the Middle Ages there were also other methods, such as halving (meditation).

 

Tab. 5: Division in the Roman number system

 

Shannon’s Roman desk calculator

The MIT Museum in Cambridge, Massachusetts, preserves a relay machine by Claude Shannon that calculates in the Roman numerical system (see Fig. 1).

Fig. 1: Shannon’s Throbac (courtesy MIT Museum, Cambridge, MA)

Throbac (Thrifty Roman-numeral backard looking computer) is a desk calculator that calculates entirely in the Roman numerical system. It performs the four basic arithmetic operations (addition, subtraction, multiplication and division) and works in the same way as an electromechanical desktop calculator used at the time. The machine accepts different spellings (IV or IIII, IL or XLIX). IIIIIV is interpreted as 0. Multiplication is carried out as a repeated addition, division as a repetitive subtraction. In multiplying 7 x 8, first the multiplicand VII is entered, then the multiplier number by number I, I, I, V. See also https://www.engage-csedu.org/find-resources/shannons-throbac.

 

References

Shannon, Claude E.: Throbac I, Bell Laboratories Memorandum, April 9, 1953 (Claude Elwood Shannon: collected papers, ed. by N. J. A. Sloane, Aaron D. Wyner, Piscataway, NJ : IEEE Press 1993, pages 695-698)

Williams, Michael Roy: A history of computing technology, IEEE Computer society press, Los Alamitos, California 1997, pages 7–8

 

Acknowledgements

Many thanks to Debbie Douglas and Ariel Weinberg from MIT.

 

Herbert Bruderer is a retired lecturer in didactics of computer science at ETH Zürich. More recently, he has been an historian of technology. bruderer@retired.ethz.ch, herbert.bruderr@bluewin.ch