Computing practitioners encounter hash functions almost every day, although they may not necessarily be the center of attention. When you install software packages or updates, the authenticity of a package is often verified with a cryptographic hash. Indeed, under the hood, everyone who browses the Web these days is using cryptographic hashes to check that the certificates used by Web servers are in order.
Non-cryptographic hash functions are also all around us. Those who write code often use dictionaries, which are usually implemented with hash functions (so much so that Perl calls them hashes). Those who use load balancers are often using hash functions to distribute the load. There are even smart algorithms for counting and deduplication of data that take advantage of non-cryptographic hashes for efficiency.
The common feature of both cryptographic and non-cryptographic hash functions is that they take inputs of data of any size and convert them to a deterministic output of specific length. Unlike encryption, this is intended to be a one-way process (that is, decryption is never required).
Cryptographic hashes have a security requirement, which is usually phrased in terms of resistance to collisions and pre-images. Indeed, for a cryptographic hash function, knowing the hash output should give you no clue about how to reconstruct the input data. In theory, you could achieve this by assigning a random output for every input and storing them in a huge table. In practice, however, clever designs for hash functions have emerged that involve bit operations, lookup tables, and repeated rounds to mix the input data.
In the case of non-cryptographic hash functions, security is not the primary requirement. Usually, you would like a hash function to map input data (for example, typically strings/IP addresses/objects) in a reasonable way across some resource (for example, linked lists, servers, or data structures). Often, reasonable means uniformly distributed outputs, or at least as close to uniform as can be achieved relatively quickly.
This desired uniformity can come under attack, giving rise to security requirements in the non-cryptographic setting; as pointed out by Scott Crosby and Dan Wallach,6 an attacker might try to mess things up by presenting inputs that all get assigned to the same resource. Simpler functions, however, are often used for the sake of speed, at least when compared with the more demanding design goals of the cryptographic hash. These non-cryptographic hash functions are the focus of this article.
Some Examples
Over the years, many hash functions have been proposed,16 but let’s look at some well-known simple examples listed in Table 1.
| Function | Pseudocode | Known for | |
|---|---|---|---|
| FNV-1a | h0 := IV = FNV Offset hi+1 := (hi ∧ bi) FNV Prime Return hfinal | Good all-rounder, decent speed and collision resistance | |
| FNV-1 | h0 := IV = FNV Offset hi+1 := (hi FNV Prime) ∧ bi Return hfinal | Similar to FNV-1a, considered inferior in specific circumstances | |
Murmur2 | SET m := 0x5bd1e995; r:=24; h0 = User chosen random ∧ Input length k := four bytes of data k := k m ∧ (k >> r) m hi+1 := (hi m) ∧ k After reading in all four-byte chunks, XOR the final h with any remaining bytes. Then, hfinal := h m ∧ (h >> 13) m ∧ (h >> 15) | Designed for excellent “avalanche” property, good collision behavior. Combines input mixing with FNV-1-style algorithm and finalization step. | |
| DJBX33A | h0 := IV = 0 or 5381 (depending on version) hi+1 := (hi 33) + bi Return hfinal | Speed and simplicity | |
| where IV is Initialization Vector, hi is intermediate hash value, and bi is the ith input byte. | |||
You can assess the behavior of a (non-cryptographic) hash function by putting it to work to see how it performs. One common use is in populating hash tables. In this case, we use modulo arithmetic to assign the inputs to one of M “buckets” by taking the hash of the input, h, and using h mod M to identify the bucket. How does the desired uniform-looking output compare with the actual results? To find out, let’s pick a few sample input sets (see Table 2) and run some code. We have selected items you would expect to populate a hash table (names, words, IP addresses) as well as something that might be troublesome (bit strings that differ from a fixed string in only one bit). This is called the Bias dataset.
| Name | Type | Description |
|---|---|---|
| Baby Names | Real text | Top 1,000 Irish baby names for 2021. Each input is one name, with lengths ranging from 3 to 11 bytes. |
| Common Words | Synthetic text | Distinct strings of varying length each composed of 20 of the most commonly used 1,000 English words. |
| Bias | Synthetic bitstring | Strings comprising 999 0xfe bytes with one 0xff byte. This results in 1,000 distinct inputs heavily biased toward one bit, with significant repeating patterns. |
| IP Addresses | Real bitstring | 32bit strings composed of unique IPv4 addresses, which had accessed a server in chronological order during 2015. |
You would assume the main goal is to ensure the hash table is filled as evenly as possible. Indeed, for a hash table implemented with a list at each bucket, it is easy enough to show that a uniform output is optimal, as this avoids long chains of data being stored in any one bucket while avoiding unused buckets. Let’s see how uniformly our hash outputs are distributed modulo M.
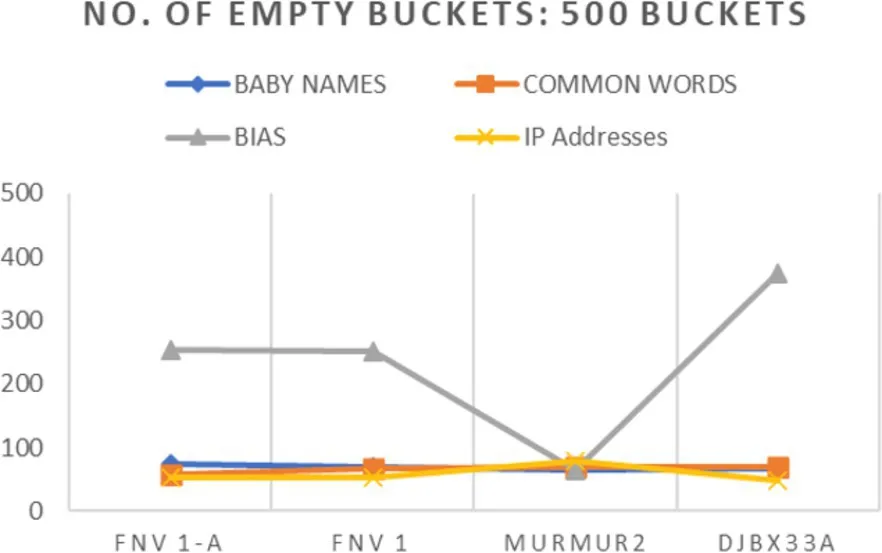
As each of these datasets comprises 1,000 lines of input, using M = 500 buckets would therefore result in a load factor of two. This means ideally, there would be two entries per bucket and no empty buckets. To get a feel for what happens in practice, see Figure 1, which shows the number of empty buckets observed for each case—about 64 empty buckets except for the Bias data, which leaves many buckets empty for three of the four hashes, and must, consequently, be crowding other buckets with data. Murmur2 is resistant to this problem; we will come back to this.
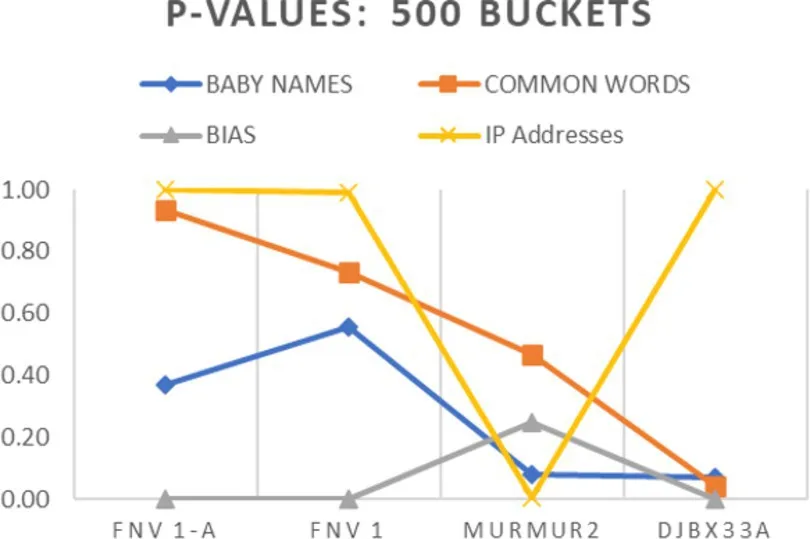
There are various ways to measure how far from uniform the distribution over the buckets is. For example, you might take a statistical approach and use a chi-squared test. In Figure 2, you can see the p-value from the test. If each output value was independently and uniformly distributed over the M buckets, then these p-values would be uniformly distributed between 0 and 1. On the other hand, repeated values close to 0 would be suspicious, which is again the case for the Bias data. This time, there is a cluster of small values for DJBX33A, a function that can be shown to preserve bit patterns in the input data. The Murmur2 values, curiously, are also lower than expected.
Interestingly, while bad behavior is evident in the Bias dataset, there are more values close to 1 for the IP Addresses set. Further investigation shows that the IP addresses contain several runs of sequential addresses that behave particularly nicely for some of the hashes. This shows that sometimes there may be gains to matching your hash function to patterns common in your data.
Taking a step back, you can, to some degree, play a game of pick-your-metric, and it might be reasonable to do so based on the requirements of your application. You can also play pick-your-M-value. For comparison, Figure 3 shows the incidence of empty buckets after picking the nearby numbers, M = 499 and M = 512. There is folklore around hash tables suggesting that an M that is prime or a power of two may be good. The original choice of M = 500 and the power of two M = 512 have similar behavior. This is because the structure of the Bias dataset results in recurring patterns in the low bits, which are preserved by working modulo numbers divisible by a power of two. A prime M, such as 499, will mitigate this sort of problem, as, in fact, will any odd values of M.

Figure 3. Empty buckets for 499 and 512 bucket sizes.
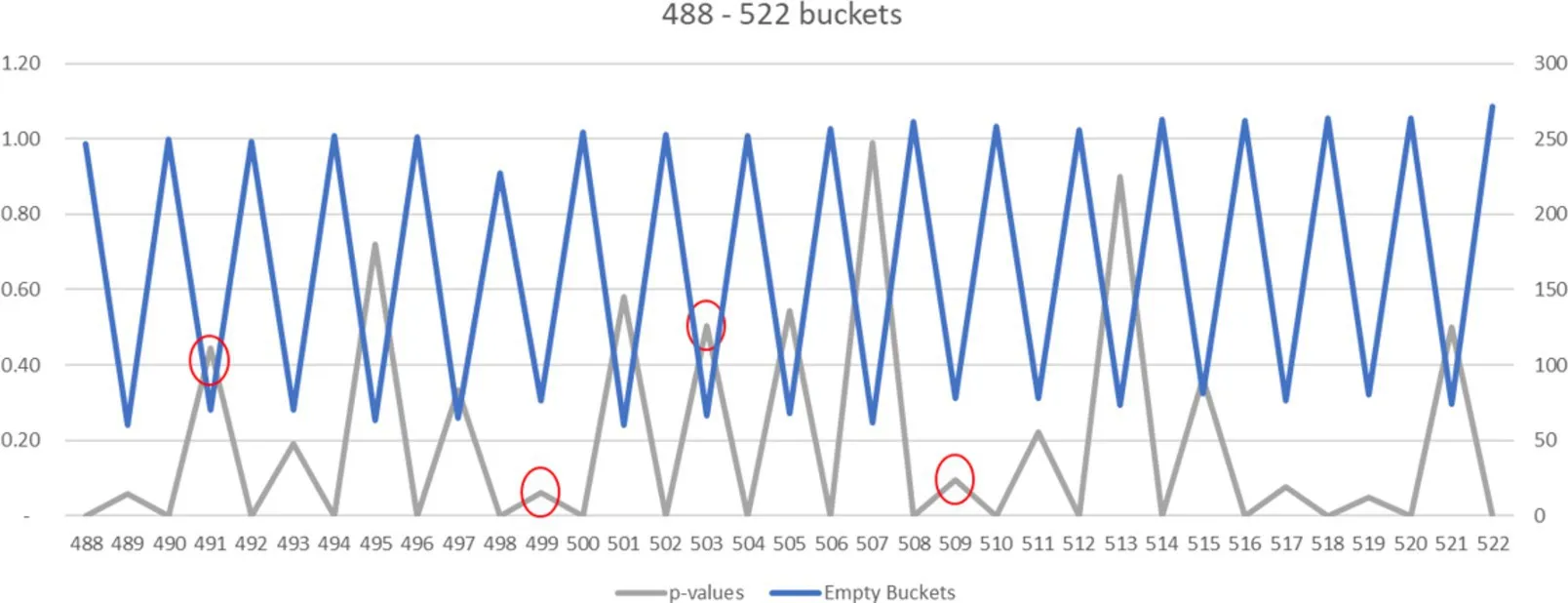
To explore this, we tried all numbers of buckets M between 488 and 522, using the Bias dataset again and combining it with FNV-1a (see Figure 4, prime numbers highlighted in red).
The number of empty buckets (blue line, axis on right-hand side) bounces quite regularly between about 60 and 270. In general, when the number of buckets is an even number, only even-numbered buckets are filled, meaning half are left empty. Likewise, any even bucket number resulted in a zero p-value (gray line in Figure 4). While odd-numbered buckets also saw a consistent number of empty buckets, p-values showed a more varied pattern. Interestingly, p-values are largest at 507 or 513 buckets, which are odd but not prime. So much for folklore.
It would appear that when using the more “real-life” datasets (that is, excluding Bias), the number of empty buckets and distributions is broadly similar for the first three hashes—both FNVs and Murmur2. It also seems you can hide some problems by using an odd value of M, although not necessarily a prime. You can also look at other metrics, such as the number of buckets with collisions, and the story stays the same.
The Avalanche Criterion
This leads to the question: Is there some general principle that could be used to design a non-cryptographic hash function? One commonly adopted measure is the avalanche criterion. To understand this, think back to the theoretical example of designing a hash function by listing every input and storing a corresponding randomly generated N-bit output. If you selected any two inputs, then the outputs would be independent of one another. In fact, each bit of the output would be set independently, meaning there would be a 50/50 chance of a flip when comparing each bit of the two outputs.
The avalanche criterion tests for this and is usually stated as: If you change one bit in your input, this change affects every bit of the output with a probability of 50%.12 For small input sizes, hash designers can test for every possible input, but for larger sizes, inputs are often randomly sampled.
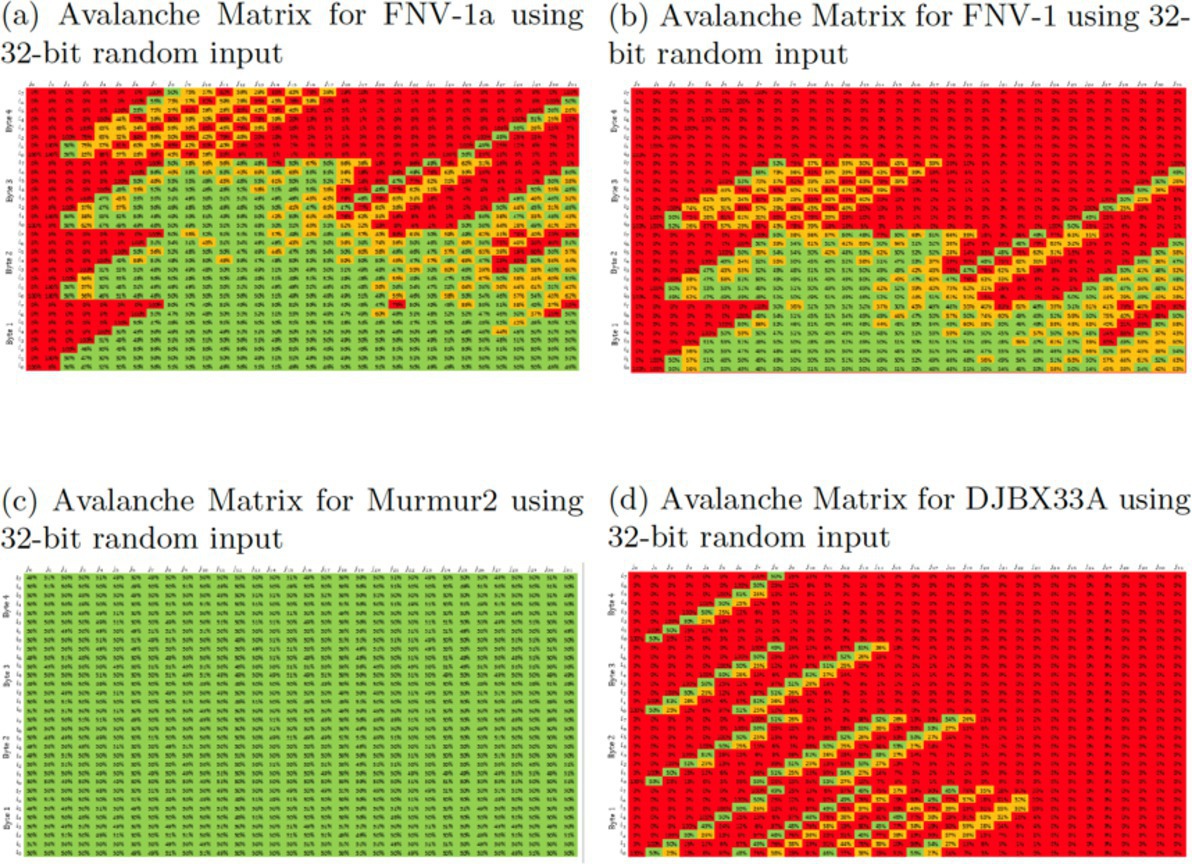
Figure 5 shows how the avalanche metric is typically evaluated. For each hash function, we have followed the work of Bret Mulvey12 and chosen random 32bit inputs and then toggled each input bit to observe the chance of each of the 32 output bits changing over 10,000 tests. The results are shown in an output matrix, colored as follows:
Green ⇒ Toggling input bit i resulted in a change to output bit j approximately 50% of the time (45%–55%). This is the ideal.
Yellow ⇒ A chance of change either 25%–45% or 55%–75%.
Red ⇒ The effect of toggling input bit i was a change to output bit j either 0%–25% or 75%–100% of the time. This is the worst-case scenario.
Murmur2 shows an impressive avalanche performance, with all entries in green. Indeed, Murmur2 was designed with the avalanche criterion in mind. Murmur2’s structure in Table 1 shows that it reads in four bytes of data at a time, which then goes through a thorough mixing step on just the current input before being combined with the previous inputs in a way that is like FNV. This mixing step essentially hides simple bit changes within a more random-looking change. Murmur2 also uses a “finalization step” to mix the output bits before producing the final hash output.
In contrast, the FNV hashes involve only two simple steps per byte of data (XOR and multiplication by prime), and DBJX33A is even simpler: taking in each byte of data, multiplying by 33, and adding to the previous value. For FNV, this results in some patterns from the input bytes being preserved in the output bytes. For example, the distinctive sawtooth pattern observed in the lower output bits of both FNV-1a and FNV-1 is because no output bit lower than the toggled input bit will ever change.
This is a result of the distribution of 1-bits in the FNV prime, which also causes the large swaths of red across the top of both FNV matrices: These represent the most recently processed byte, where changes to it have not had a chance to dissipate into all the bits. For DJBX33A, multiplying by 33, or 0b00100001, is equivalent to shifting five places to the left and then adding the original byte. Therefore, a lot of information about the input is preserved mod 32, and it requires many runs through the algorithm to propagate changes to the higher output bits. These issues can be clearly observed in Figure 5.
Although Murmur2 shows much better behavior in terms of the avalanche criterion, its collision resistance and distribution performance on these datasets was not so exceptional, except for the Bias dataset. That dataset was constructed to have many single-bit input differences, which is exactly the type of change targeted by the avalanche criterion. It is possible to produce a challenging dataset for Murmur2 by applying the inverse of its input-mixing step to the Bias dataset. This is a general lesson—every hash function has a dataset that it will find challenging, if the data is selected carefully enough.
Avalanche is an interesting criterion, but it targets a specific form of input differences, where single-bit changes are important. Given that this does not seem so common in real data, let’s take a quick trip through history to understand how the avalanche criterion became interesting for designers.
Some History
Some early references to something like the avalanche criterion come up when discussing S-boxes (substitution boxes) in the Data Encryption Standard (DES) cipher. One strategy, when attacking a cipher, can be to make small changes to the input and then attempt to learn about the key. Here, avalanche is described as ensuring that changing a single bit of the input will change at least two bits in the S-box output,10 which in turn leads to an avalanche of changed bits as the internal rounds of the DES cipher are repeated. In Applied Cryptography, when analyzing the DES system, Bruce Schneier describes the cryptographic benefit of this: “By allowing one bit to affect two substitutions, the dependency of the output bits on the input bits spreads faster. This is called an avalanche effect. DES is designed to reach the condition of having every bit of the ciphertext depend on every bit of the plaintext and every bit of the key as quickly as possible.”13
These original uses of avalanche are clearly in a cryptographic context and might reasonably be applied to cryptographic hashes, where similar security requirements are present. The question now is: How has avalanche migrated from a cryptographic background into the non-cryptographic world? We looked at several papers to see where references to avalanche as a criterion for non-cryptographic hashes may have originated and progressed through the literature.
For example, in their paper, “Novel Non-Cryptographic Hash Functions for Networking and Security Applications on FPGA,” Claesen, et al. state, “Non-cryptographic hashes for applications such as Bloom filters, hash tables, and sketches must be fast, uniformly distributed and must have excellent avalanche properties.”4 Two papers are cited in support of this (Bloom3 and Cormode and Muthukrishnan5), but neither one directly mentions avalanche.
Similarly, in “Performance of the Most Common Non-Cryptographic Hash Functions,” Estébanez, et al. mention that the avalanche effect is important for non-cryptographic hash functions, providing several references.7 One is to Hashing in Smalltalk: Theory and Practice, Valloud’s book on assessing hash functions, which is actually lukewarm on the avalanche criterion: “Although the avalanche test is quite popular, note that… it says nothing of the distribution of the actual hash values. In particular, it is quite possible to construct hash functions of horrific quality that nevertheless effortlessly achieve general avalanche.”16
Another common reference is Uzgalis’s “Hashing Concepts and the Java Programming Language” from 1996.15 The author does note that one of the two criteria used to choose a candidate hash for Java was a mixing criterion: “The algorithm must guarantee that a change in any single bit of a key should result in an equally probable change to every bit of the hash value.” This is clearly the avalanche criterion, but the author goes on to make a distinction between randomized-looking output and uniformly distributed outputs. Again, avalanche is vital only for those in search of a random result.
In fact, in all the applicable papers we identified, the avalanche criterion is either presented as a goal in itself or provides references that either are dead ends or lead to guarded discussions about avalanche’s universal applicability.1,8,9
Repackaging Avalanche
Another challenge that arises with avalanche is that it is really targeting output that is uniform over, say, a 32bit output. What the application would usually like, however, is an output that is uniform over the M resources. In fact, it is impossible to pack a uniform 32bit output uniformly into M buckets unless M is a power of two, which brings its own drawbacks, as seen earlier. This problem was recognized some years ago for random-number generators and is described as modulo bias. This resulted in the introduction of functions such as arc4random_uniform(), which use extra random bits to resolve the bias. Work is ongoing to optimize fixes for modulo bias for random numbers.11 The situation for hash functions is somewhat less developed, probably because the input data itself can always be a source of non-uniformity.
Some Final Thoughts
Although cryptographic and non-cryptographic hash functions are everywhere, there seems to be a gap in how they are designed. Lots of criteria exist for cryptographic hashes motivated by various security requirements, but on the non-cryptographic side there is a certain amount of folklore that, despite the long history of hash functions, has not been fully explored. While targeting a uniform distribution makes a lot of sense for real-world datasets, it can be a challenge when confronted by a dataset with particular patterns.
Avalanche may be an important criterion for cryptographic hash functions, but its focus on randomizing the relationship between input and output may not have a big impact on distribution of entries in a hash table. Distributing outputs in a hash table raises the long-debated question of whether to choose your M to be a prime of power of two but does not generally consider the option of simply using an odd number.
This evidence all fits with the idea that non-cryptographic hash functions perhaps deserve more attention. Some already think that too much is being asked of individual cryptographic hashes: Maybe a one-size-fits-all approach is not workable.14 Another approach has been to design hashes targeting a middle ground; these would have some security requirements but maintain the speed and efficiency of a non-cryptographic hash—for example, SipHash.2 Perhaps studying hashes for a range of specific situations will help clarify how (or if) we should evaluate non-cryptographic hash functions in general.





Join the Discussion (0)
Become a Member or Sign In to Post a Comment