
Napier’s rods, also called Napier’s bones (see Figure 1), were invented at the beginning of the 17th century. They have been used for multiplications and divisions until the 19th century. There were various forms, e.g. rotating cylinders.

The set consists of 25 wooden rods. They were used primarily for multiplication and for calculating square and cube numbers.
Credit: Nisse Cronestrand, Tekniska Museet, Stockholm
Operating Instructions for Napier’s Bones
Napier’s multiplication and division rods, deriving from the basic multiplication table, simplify calculations considerably. They were also built into several mechanical calculating aids as rotating drums. The intermediate results are read from the diagonal grid and added by hand, taking account of the tens carry. According to the model, the diagonals run from the lower left to the upper right or from the upper left to the lower right. The tens are at the upper left or the lower left, respectively, and the ones at the lower right or the upper right, respectively.
See also How Does One Multiply with Napier’s Rods? | blog@CACM | Communications of the ACM.
Division
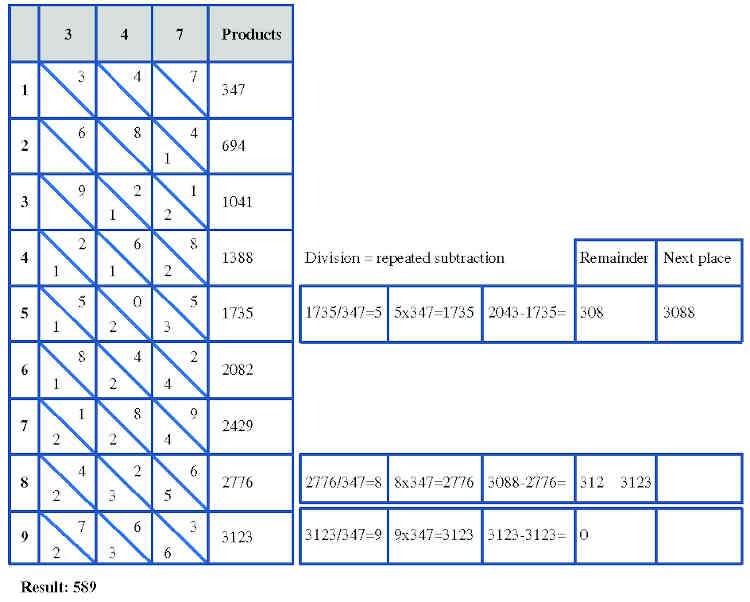
Example 3: 204,383: 347 = 589 (see Fig. 2)
- Lay the rods with the numerals of the divisor next to each other. Place the basic rod with the numerical column 1 to 9 to the left of these.
- Read off how many times 347 goes into the first numbers 2043 of the dividend (5x). The next lower value with a whole number quotient is 1735, and the next higher value 2082 is too high.
- Then subtract 1735 (5 × 347) from 2043. Add the next digit (8) of the dividend to the remainder (308).
- Control how often 347 goes into 3088 (8x). The next lower value with a whole number quotient is 2776.
- Then subtract 2776 (8 × 347) from 3088. Add the last digit (3) of the dividend to the remainder (312).
- For the division 347 into 3123, this gives the value 9.
- The final result is 589.
Napier’s bones
Example: 204,383: 347 = 589
How often the divisor goes into the dividend is read off from the diagonal grid.
Credit: Bruderer Informatik, CH-9401 Rorschach, Switzerland
A few selected examples of rotating drums (see Figures 3 and 4).

The German Kaspar Schott transformed Napier’s bones into 12 rotatable cylinders
that include multiplication tables with the numerals 1 to 9 and thus build upon the Pythagorean table.
This instrument also enables division and extracting roots. The device is a replica.
Credit: Science Museum, London/Science & Society Picture Library

This calculator of Michel Rous from Paris (1869) comprises eight rotating Napier’s bones
and a nine-place Chinese abacus.
Credit: Technisches Museum Wien, Vienna
Source
Bruderer, Herbert: Milestones in Analog and Digital Computing, Springer Nature Switzerland AG, Cham, 3rd edition 2020, 2 volumes, 2113 pages, 715 illustrations, 151 tables
https://www.springer.com/de/book/9783030409739 (translated by Dr. John McMinn)
Herbert Bruderer is a retired lecturer in didactics of computer science at ETH Zurich. More recently, he has been an historian of technology. bruderer@retired.ethz.ch, herbert.bruderer@bluewin.



Join the Discussion (0)
Become a Member or Sign In to Post a Comment