Much has been written about the transition of commodity microprocessors from single-core to multicore chips, a trend most apparent in CPU processor families. Commodity PCs are now typically built with CPUs containing from two to eight cores, with even higher core counts on the horizon. These chips aim to deliver higher performance by exploiting modestly parallel workloads arising from either the need to execute multiple independent programs or individual programs that themselves consist of multiple parallel tasks, yet maintain the same level of performance as single-core chips on sequential workloads.
A related architectural trend is the growing prominence of throughput-oriented microprocessor architectures. Processors like Sun’s Niagara and NVIDIA’s graphics processing units, or GPUs, follow in the footsteps of earlier throughput-oriented processor designs but have achieved far broader use in commodity machines. Broadly speaking, they focus on executing parallel workloads while attempting to maximize total throughput, even though sacrificing the serial performance of a single task may be required. Though improving total throughput at the expense of increased latency on individual tasks is not always a desirable trade-off, it is unquestionably the right design decision in many problem domains that rely on parallel computations, including real-time computer graphics, video processing, medical-image analysis, molecular dynamics, astrophysical simulation, and gene sequencing.
Modern GPUs are fully programmable and designed to meet the needs of a problem domain—real-time computer graphics—with tremendous inherent parallelism. Furthermore, real-time graphics places a premium on the total amount of work that can be accomplished within the span of a single frame (typically lasting 1/30 second). Due to their historical development, GPUs have evolved as exemplars of throughput-oriented processor architecture. Their emphasis on throughput optimization and their expectation of abundant available parallelism is more aggressive than many other throughput-oriented architectures. They are also widely available and easily programmable. NVIDIA released its first GPU supporting the CUDA parallel computing architecture in 2006 and is currently shipping its third-generation CUDA architecture, code-named “Fermi,”24 released in 2010 in the Tesla C2050 and other processors.
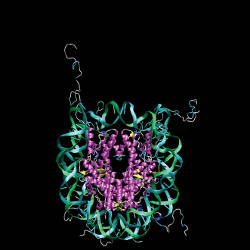
Figure 1 is a nucleosome structure (with 25,095 atoms) used in benchmarking the AMBER suite of molecular dynamics simulation programs. Many core computations performed in molecular dynamics are intrinsically parallel, and AMBER recently added CUDA-accelerated computations (http://ambermd.org/gpus/). Its Generalized Born implicit solvent calculation for this system running on the eight cores of a dual four-core Intel Xeon E5462 executes at a rate of 0.06 nanoseconds of simulation time per day of computation. The same calculation running on an NVIDIA Tesla C2050 executes the simulation at a rate of 1.04 ns/day, roughly 144 times more work per day than a single sequential core and just over 17 times the throughput of all eight cores.
Using the GPU as a case study, this article explores the fundamental architectural design decisions differentiating throughput-oriented processors from their more traditional latency-oriented counterparts. These architectural differences also lead to an approach to parallel programming that is qualitatively different from the parallel thread models prevalent on today’s CPUs.
Throughput-Oriented Processors
Two fundamental measures of processor performance are task latency (time elapsed between initiation and completion of some task) and throughput (total amount of work completed per unit time). Processor architects make many carefully calibrated trade-offs between latency and throughput optimization, since improving one could degrade the other. Real-world processors tend to emphasize one over the other, depending on the workloads they are expected to encounter.
Traditional scalar microprocessors are essentially latency-oriented architectures. Their goal is to minimize the running time of a single sequential program by avoiding task-level latency whenever possible. Many architectural techniques, including out-of-order execution, speculative execution, and sophisticated memory caches, have been developed to help achieve it. This traditional design approach is predicated on the conservative assumption that the parallelism available in the workload presented to the processor is fundamentally scarce. Single-core scalar CPUs typified by the Intel Pentium IV were aggressively latency-oriented. More recent multicore CPUs (such as the Intel Core2 Duo and Core i7) reflect a trend toward somewhat less-aggressive designs that expect a modest amount of parallelism.
Throughput-oriented processors, in contrast, arise from the assumption that they will be presented with workloads in which parallelism is abundant. This fundamental difference leads to architectures that differ from traditional sequential machines. Broadly speaking, throughput-oriented processors rely on three key architectural features: emphasis on many simple processing cores, extensive hardware multithreading, and use of single-instruction, multiple-data, or SIMD, execution. Aggressively throughput-oriented processors, exemplified by the GPU, willingly sacrifice single-thread execution speed to increase total computational throughput across all threads.
No successful processor can afford to optimize aggregate task throughput while completely ignoring single-task latency or vice versa. Different processors may also vary in the degree they emphasize one over the other; for instance, individual throughput-oriented architectures may not use all three architectural features just listed. Also worth noting is that several architectural strategies, including pipelining, multiple issue, and out-of-order execution, avoid task-level latency by improving instruction-level throughput.
Hardware multithreading. A computation in which parallelism is abundant can be decomposed into a collection of concurrent sequential tasks that may potentially be executed in parallel, or simultaneously, across many threads. We view a thread as a virtualized scalar processor, typically meaning each thread has a program counter, register file, and associated processor state. A thread is thus able to execute the instruction stream corresponding to a single sequential task. Note this model of threads says nothing about the way concurrent threads are scheduled; for instance, whether they are scheduled fairly (any thread ready to run is eventually executed) is a separate issue.
It is well known that multithreading, whether in hardware31 or software,4 provides a way of tolerating latency. If a given thread is prevented from running because it is waiting for an instruction to make its way through a pipelined functional unit, data to arrive from external DRAM or some other event, a multithreaded system can allow another unblocked thread to run. That is, the long-latency operations of a single thread can be hidden or covered by ready-to-run work from another thread. This focus on tolerating latency, where processor utilization does not suffer simply because a fraction of the active threads are blocked, is a hallmark of throughput-oriented processors.
Hardware multithreading as a design strategy for improving aggregate performance on parallel workloads has a long history. The peripheral processors of the Control Data Corp. CDC 6600 developed in the 1960s and the Heterogeneous Element Processor (HEP) system28 developed in the late 1970s are notable examples of the early use of hardware multithreading. Many more multithreaded processors have been designed over the years31; for example, the Tera,1,2 Sun Niagara,18 and NVIDIA GPU22 architectures all use aggressive multithreading to achieve high-throughput performance on parallel workloads, all with interleaved multi-threading.21 Each is capable of switching between threads at each cycle. Thus the execution of threads is interleaved at extremely fine granularity, often at the instruction level.
Blocking multithreading is a coarser-grain strategy in which a thread might run uninterrupted until encountering a long-latency operation, at which point a different thread is selected for execution. The streaming processors Imagine,16 Merrimac,9 and SPI Storm17 are notable examples of throughput-oriented architectures adopting this strategy. These machines explicitly partition programs into bulk load/store operations on entire data blocks and “kernel” tasks in which memory accesses are restricted to on-chip blocks loaded on their behalf. When a kernel finishes processing its on-chip data, a different task in which required memory blocks have been loaded onto the chip is executed. Overlapping the bulk data transfer for one or more tasks while another is executing hides memory-access latency. Strategic placement of kernel boundaries where context switches occur can also substantially reduce the amount of state that must be retained between task executions.
A third strategy called simultaneous multithreading30 allows different threads to simultaneously issue instructions to independent functional units and is used to improve the efficiency of superscalar sequential processors without having to find instruction-level parallelism within a single thread. It is likewise used by NVIDIA’s Fermi architecture24 in place of intra-thread dual issue to achieve higher utilization.
The design of the HEP,28 Tera,2 and NVIDIA G8022 processors highlights an instructive characteristic of some throughput-oriented processors: none provides a traditional cache for load/store operations on external memory, unlike latency-oriented processors (such as typical CPUs) that expend substantial chip area on sophisticated cache subsystems. These machines are able to achieve high throughput in the absence of caches because they assume there is sufficient parallel work available to hide the latency of off-chip memory accesses. Unlike previous NVIDIA processors, the Fermi architecture provides a cache hierarchy for external memory accesses but still relies on extensive multithreading for latency tolerance.
Many simple processing units. The high transistor density in modern semiconductor technologies makes it feasible for a single chip to contain multiple processing units, raising the question of how to use the available area on the chip to achieve optimal performance: one very large processor, a handful of large processors, or many small processors?
Designing increasingly large single-processor chips is unattractive.6 The strategies used to obtain progressively higher scalar performance (such as out-of-order execution and aggressive speculation) come at the price of rapidly increasing power consumption; incremental performance gains incur increasingly large power costs.15 Thus, while increasing the power consumption of a single-threaded core is physically possible, the potential performance improvement from more aggressive speculation appears insignificant by comparison. This analysis has led to an industrywide transition toward multicore chips, though their designs remain fundamentally latency-oriented. Individual cores maintain roughly comparable scalar performance to earlier generations of single-core chips.
Throughput-oriented processors achieve even higher levels of performance by using many simple, and hence small, processing cores.10 The individual processing units of a throughput-oriented chip typically execute instructions in the order they appear in the program, rather than trying to dynamically reorder instructions for out-of-order execution. They also generally avoid speculative execution and branch prediction. These architectural simplifications often reduce the speed with which a single thread completes its computation. However, the resulting savings in chip area allow for more parallel processing units and correspondingly higher total throughput on parallel workloads.
SIMD execution. Parallel processors frequently employ some form of single-instruction, multiple-data, or SIMD, execution12 to improve their aggregate throughput. Issuing a single instruction in a SIMD machine applies the given operation to potentially many data operands; SIMD addition might, for example, perform pairwise addition of two 64-element sequences. As with multi-threading, SIMD execution has a long history dating to at least the 1960s.
Aggressively throughput-oriented processors, exemplified by the GPU, willingly sacrifice single-thread execution speed to increase total computational throughput across all threads.
Most SIMD machines can be classified into two basic categories. First is the SIMD processor array, typified by the ILLIAC IV developed at the University of Illinois,7 the Thinking Machines CM-2,29 and the MasPar Computer Corp. MP-1.5 All consisted of a large array of processing elements (hundreds or thousands) and a single control unit that would consume a single instruction stream. The control unit would broadcast each instruction to all processing elements that would then execute the instruction in parallel.
The second category is the vector processor, exemplified by the Cray-125 and numerous other machines11 that augment a traditional scalar instruction set with additional vector instructions operating on data vectors of some fixed width—64-element vectors in the Cray-1 and four-element vectors in the most current vector extensions (such as the x86 Streaming SIMD Extensions, or SSE). The operation of a vector instruction, like vector addition, may be performed in a pipelined fashion (as on the Cray-1) or in parallel (as in current SSE implementations). Several modern processor families, including x86 processors from Intel and AMD and the ARM Cortex-A series, provide vector SIMD instructions that operate in parallel on 128-bit (such as four 32-bit integer) values. Programmable GPUs have long made aggressive use of SIMD; current NVIDIA GPUs have a SIMD width of 32. Many recent research designs, including the Vector IRAM,19 SCALE,20 and Imagine and Merrimac streaming processors,9,16 have also used SIMD architectures to improve efficiency.
SIMD execution is attractive because, among other things, it increases the amount of resources that can be devoted to functional units rather than control logic. For instance, 32 floating-point arithmetic units coupled with a single control unit takes less chip area than 32 arithmetic units with 32 separate control units. The desire to amortize the cost of control logic over numerous functional units was the key motivating factor behind even the earliest SIMD machines.7
However, devoting less space to control comes at a cost. SIMD execution delivers peak performance when parallel tasks follow the same execution trace and can suffer when heterogeneous tasks follow completely different execution traces. The efficiency of SIMD architectures depends on the availability of sufficient amounts of uniform work. In practice, sufficient uniformity is often present in abundantly parallel workloads, since it is more likely that a pool of 10,000 concurrent tasks consists of a small number of task types rather than 10,000 completely disparate computations.
GPUs
Programmable GPUs are the leading exemplars of aggressively throughput-oriented processors, taking the emphasis on throughput further than the vast majority of other processors and thus offering tremendous potential performance on massively parallel problems.13
Historical perspective. Modern GPUs have evolved according to the needs of real-time computer graphics, two aspects of which are of particular importance to understanding the development of GPU designs: it is an extremely parallel problem, and throughput is its paramount measure of performance.
Visual applications generally model the environments they display through a collection of geometric primitives, with triangles the most common. The most widely used techniques for producing images from these primitives proceed through several stages where processing is performed on each triangle, triangle corner, and pixel covered by a triangle. At each stage, individual triangles/vertices/pixels can be processed independently of all others. An individual scene can easily paint millions of pixels at a time, thus generating a great deal of completely parallel work. Furthermore, processing an element generally involves launching a thread to execute a program—usually called a shader—written by the developer. Consequently, GPUs are specifically designed to execute literally billions of small user-written programs per second.
Most real-time visual applications are designed to run at a rate of 3060 frames per second. A graphics system is therefore expected to generate, render, and display images of visually complex worlds within 33ms. Since it must complete many millions of independent tasks within this timeframe, the time to complete any one of these tasks is relatively unimportant. But the total amount of work that can be completed within 33ms is of great importance, as it is generally closely correlated with the visual richness of the environment being displayed.
Their role in accelerating real-time graphics has also made it possible for GPUs to become mass-market devices, and, unlike many earlier throughput-oriented machines, they are also widely available. Since late 2006, NVIDIA has shipped almost 220 million CUDA-capable GPUs—several orders of magnitude more than historical massively parallel architectures like the CM-2 and MasPar machines.
NVIDIA GPU architecture. Beginning with the G80 processor released in late 2006, all modern NVIDIA GPUs support the CUDA architecture for parallel computing. They are built around an array of multiprocessors, referred to as streaming multiprocessors, or SMs.22,24 Figure 2 diagrams a representative Fermi-generation GPU like the GF100 processor used in the Tesla C2050. Each multiprocessor supports on the order of a thousand co-resident threads and is equipped with a large register file, giving each thread its own dedicated set of registers. A high-end GPU with many SMs can thus sustain tens of thousands of threads simultaneously. Multiprocessors contain many scalar processing elements that execute the instructions issued by the running threads. Each multiprocessor also contains high-bandwidth, low-latency on-chip shared memory, while at the same time providing its threads with direct read/write access to off-chip DRAM. The Fermi architecture can configure its 64KB of per-SM memory as either a 16KB L1 cache and 48KB RAM or a 48KB L1 cache and 16KB RAM. It also provides a global 768KB L2 cache shared by all SMs. The table here summarizes the capacity of a single SM for the three generations of NVIDIA CUDA-capable GPUs.
The SM multiprocessor handles all thread creation, resource allocation, and scheduling in hardware, interleaving the execution of threads at the instruction-level with essentially zero overhead. Allocation of dedicated registers to all active threads means there is no state to save/restore when switching between threads. With all thread management performed in hardware, the cost of employing many threads is minimal. For example, a Tesla C2050 executing the increment() kernel in Figure 3 will create, execute, and retire threads at a rate of roughly 13 billion threads/sec.
To manage its large population of threads efficiently, the GPU employs a single-instruction, multiple-thread, or SIMT, architecture in which threads resident on a single SM are executed in groups of 32, called warps, each executing a single instruction at a time across all its threads. Warps are the basic unit of thread scheduling, and in any given cycle the SM is free to issue an instruction from any runnable warp. The threads of a warp are free to follow their own execution path, and all such execution divergence is handled automatically in hardware. However, it is obviously more efficient for threads to follow the same execution path for the bulk of the computation. Different warps may follow different execution paths without penalty.
While SIMT architectures share many performance characteristics with SIMD vector machines, they are, from the programmer’s perspective, qualitatively different. Vector machines are typically programmed with either vector intrinsics explicitly operating on vectors of some fixed width or compiler auto-vectorization of loops. In contrast, SIMT machines are programmed by writing a scalar program describing the action of a single thread. A SIMT machine implicitly executes groups of independent scalar threads in a SIMD fashion, whereas a vector machine explicitly encodes SIMD execution in the vector operations in the instruction stream it is given.
CUDA programming model. The CUDA programming model23,26 provides a minimalist set of abstractions for parallel programming on massively multithreaded architectures like the NVIDIA GPU. A CUDA program is organized into one or more threads executing on a host processor and one or more parallel kernels that can be executed by the host thread(s) on a parallel device.
Individual kernels execute a scalar sequential program across a set of parallel threads. The programmer organizes the kernel’s threads into thread blocks, specifying for each kernel launch the number of blocks and number of threads per block to be created. CUDA kernels are thus similar in style to a blocked form of the familiar single-program, multiple-data, or SPMD, paradigm. However, CUDA is somewhat more flexible than most SPMD systems in that the host program is free to customize the number of threads and blocks launched for a particular kernel at each invocation. A thread block is a group of parallel threads that may synchronize with one another at a per-block barrier and communicate among themselves through per-block shared memory. Threads from different blocks may coordinate with one another via atomic operations on variables in the global memory space visible to all threads. There is an implicit barrier between successive dependent kernels launched by the host program.
The NVIDIA CUDA Toolkit (http://www.nvidia.com/cuda) includes a C compiler equipped with a small set of language extensions for writing CUDA programs. Figure 3 sketches a simple CUDA program fragment illustrating these extensions. The _global_ modifier indicates the increment() function is a kernel entry point and may be called only when launching a kernel. Unmodified functions and those functions explicitly marked _host_ are normal C functions. The host program launches kernels using the function-call-like syntax increment<<<B, T>>>(...), indicating the function increment() will be launched in parallel across B blocks of T threads each. The blocks of a kernel are numbered using two-dimensional indices visible to the kernel as the special variables blockIdx.x and blockIdx.y, ranging from 0 to gridDim.x-1 and gridDim.y-1, respectively. Similarly, the threads of a block are numbered with three-dimensional indices threadIdx.x, threadIdx.y, threadIdx.z; the extent of the block in each dimension is given by blockDim.x, blockDim.y, and blockDim.z.
The function parallel _ increment() accepts an array x of n elements and launches a parallel kernel with at least one thread for each element organized into blocks of 256 threads each. Since the data in the example is one-dimensional, the code in Figure 3 uses one-dimensional indices. Also, since every thread in this computation is completely independent, deciding to use 256 threads per block in our implementation was largely arbitrary. Every thread of the kernel computes a globally unique index i from its local threadIdx and the blockIdx of its block. It increments the value of xi by 1 if i < n—a conditional check required since n need not be a multiple of 256.
Throughput-Oriented Programming
Scalability is the programmer’s central concern in designing efficient algorithms for throughput-oriented machines. Today’s architectural trends clearly favor increasing parallelism, and effective algorithmic techniques must scale with hardware parallelism. Some techniques suitable for four parallel threads may be entirely unsuitable for 4,000 parallel threads. Running thousands of threads at a time, GPUs are a powerful platform for exploring scalable algorithms and a leading indicator for algorithm design on future throughput-oriented architectures.
Abundant parallelism. Throughput-oriented programs must expose substantial amounts of fine-grain parallelism, fulfilling the expectations of the architecture. Exploiting multicore CPUs obviously requires exposing parallelism as well, but a programmer’s mental model of parallelism on a throughput-oriented processor is qualitatively different from multicore. A four-core CPU can be fully utilized by four to eight threads. Thread creation and scheduling are computationally heavyweight, since they can involve the saving and restoration of processor state and relatively expensive calls to the operating system kernel. In contrast, a GPU typically requires thousands of threads to cover memory latency and reach full utilization, while thread scheduling is essentially without cost.
Consider computing the product y=Ax, where A is a n×n matrix, and x is an n-element vector. For sparse problems, because the vast majority of matrix entries is 0, A is best represented using a data structure that stores only its non-zero elements. The algorithm for sparse matrix-vector multiplication (SpMV) would look like this:
Since each row is processed independently, a simple CUDA implementation would assign a separate thread to each row. For large matrices, this could easily expose millions of threads of parallelism. However, for smaller matrices with only a few thousand rows, this level of parallelism might be insufficient, so an efficient implementation could instead assign multiple threads to process each row. In the most extreme case, each non-zero element could be assigned to a separate thread.
GPUs are specifically designed to execute literally billions of small user-written programs per second.
Figure 4 plots an experiment measuring the performance of three different parallel granularities: one thread/row, 32 threads/row, and one thread/non-zero.3 These tests use synthetic matrices with a constant number of entries distributed across a variable number of rows ranging from one row with four million entries on the left to four million rows of one entry each on the right. The maximal parallelism resulting from assigning one thread per non-zero element yields the most efficient implementation when there are few rows but suffers from lower absolute performance due to its need for inter-thread synchronization. For intermediate row counts, assigning 32 threads per row is the best solution, while assigning one thread per row is best when the number of rows is sufficiently large.
Calculation is cheap. Computation generally costs considerably less than memory transfers, particularly external memory transfers that frequently require hundreds of cycles to complete. The fact that the cost of memory access has continued to increase and is now quite high relative to the cost of computation is often referred to as the “memory wall.” The energy required to move data between the chip and external DRAM is also far higher than required to operate an on-chip functional unit. In a 45nm process, a 64-bit integer addition unit expends roughly 1pJ (picojoule), and a 64-bit floating point fused multiply add, or FMA, unit requires around 100pJ. In contrast, reading a 64-bit value from external DRAM requires on the order of 2,000pJ.8
The high relative cost of accessing memory affects both latency and throughput-oriented processors, since the cost is the result of the physical properties of semiconductor technology. However, the performance consequences of external memory references for throughput-oriented processors can be more significant; these processors are designed to reach a higher peak computational throughput and may have a higher peak throughput-to-bandwidth ratio than latency-oriented processors. More important, they seek to tolerate rather than avoid latency. To hide the latency of frequent movement of data to/from main memory requires either more threads or more work per thread, generally requiring larger data sets.
The best performance is typically achieved when calculation is more common than data access. Performing roughly 10 to 20 operations per word of data loaded from memory is ideal, and it may be preferable to locally recompute values rather than store frequently needed values in external memory. Consider a simple example of computing a moderately expensive function like sin θ for 256 unique values of θ. Tabulating all 256 possible values would require little space, but accessing them from external memory would require hundreds of cycles. In the same amount of time, a thread could execute perhaps 50 to 100 instructions that could be used to compute the result and leave the memory bandwidth available for other uses.
Divide and conquer. Divide-and-conquer methods often yield effective parallel algorithms, even for apparently serial problems. Consider the merging of two sorted sequences A and B, a common problem for which most computer science students learn a sequential solution like this:
A related divide-and-conquer algorithm picks an element s from either A or B and partitions both sequences into those elements A1,B1 that are less than s and elements A2,B2 that are not less than s. Having split the input sequences, constructing the merged sequence is simply a matter of recursively merging Ai with Bi. The code for doing it would look like this:
This approach is reminiscent of quicksort though more efficient since A and B are both sorted. If s is drawn from A, “partitioning” A is trivial, since the elements less than s are simply those preceding s, and the corresponding point at which s splits B can be found through binary search.
This divide-and-conquer method can lead to an inherently parallel algorithm by picking a sorted sequence of k splitting elements s1, …, sk. These splitters partition both A and B into k+1 subsequences that can be merged independently like this:
Since each recursive merge is independent, this is an intrinsically parallel algorithm. Merge algorithms of this form have been used in the parallel programming literature for decades14 and can be used to build efficient merge sort routines in CUDA.27
Hierarchical synchronization. More often than not, parallel threads must synchronize with one another at various times, but excessive synchronization can undermine the efficiency of parallel programs. Synchronization must be treated carefully on massively parallel throughput-oriented processors where thousands of threads could potentially contend for a lock.
To avoid unnecessary synchronization, threads should synchronize hierarchically, keeping parallel computations independent as long as possible. When parallel programs are decomposed hierarchically, as in divide-and-conquer methods, the synchronization of threads can also be organized in a hierarchical fashion. For example, when evaluating merge3(A,B) earlier, each recursive parallel merge step can proceed independently of all the others. Any synchronization required within these subtasks can be localized to the subtasks. Only at the end, when all subsequent operations are merged, must the parallel subtasks be synchronized with one another. Organizing synchronization hierarchically also aligns well with the physical cost of synchronizing threads spread across different sections of a given system. It is natural to expect that threads executing on a single core can be synchronized much more cheaply than threads spread across an entire processor, just as threads on a single machine can be synchronized more cheaply than threads across the multiple nodes of a cluster.
Conclusion
The transition from single-core to multicore processors and the increasing use of throughout-oriented architectures signal greater emphasis on parallelism as the driving force for higher computational performance. Yet these two kinds of processors differ in the degree of parallelism they expect to encounter in a typical workload. Throughput-oriented processors assume parallelism is abundant, rather than scarce, and their paramount design goal is maximizing total throughput of all parallel tasks rather than minimizing the latency of a single sequential task.
Emphasizing total throughput over the running time of a single task leads to a number of architectural design decisions. Among them, the three primary architectural trends typical of throughput-oriented processors are hardware multithreading, many simple processing elements, and SIMD execution. Hardware multithreading makes managing the expected abundant parallelism cheap. Simple in-order cores forgo out-of-order execution and speculation, and SIMD execution increases the ratio of functional units to control logic. Simple core design and SIMD execution reduce the area and power cost of control logic, leaving more resources for parallel functional units.
These design decisions are all predicated on the assumption that sufficient parallelism exists in the workloads the processor is expected to handle. The performance of a program with insufficient parallelism may therefore suffer. A fully general-purpose chip (such as a CPU) cannot afford to aggressively trade for increased total performance at the cost of single-thread performance. The spectrum of workloads presented to it is simply too broad, and not all computations are parallel. For computations that are largely sequential, latency-oriented processors perform better than throughput-oriented processors. On the other hand, a processor specifically intended for parallel computation can accept this trade-off and realize significantly greater total throughput on parallel problems as a result.
As the differences between these architectures appear durable rather than transient, the ideal system is thus heterogeneous, where a latency-oriented processor (such as a CPU) and a throughput-oriented processor (such as a GPU) work in tandem to address the heterogeneous workloads presented to them.
Figures
 Figure 1. Throughput-oriented processors like the NVIDIA Tesla C2050 deliver substantially higher performance on intrinsically parallel computations, including molecular dynamics simulations.
Figure 1. Throughput-oriented processors like the NVIDIA Tesla C2050 deliver substantially higher performance on intrinsically parallel computations, including molecular dynamics simulations.
 Figure 2. NVIDIA GPU consisting of an array of multithreaded multiprocessors.
Figure 2. NVIDIA GPU consisting of an array of multithreaded multiprocessors.
 Figure 3. Trivial CUDA C kernel for incrementing each element of an array.
Figure 3. Trivial CUDA C kernel for incrementing each element of an array.
 Figure 4. Double-precision throughput of SpMV strategies on an NVIDIA GeForce GTX 285 GPU; all matrices have exactly 4 x 210 nonzeros but differing row counts.
Figure 4. Double-precision throughput of SpMV strategies on an NVIDIA GeForce GTX 285 GPU; all matrices have exactly 4 x 210 nonzeros but differing row counts.








Join the Discussion (0)
Become a Member or Sign In to Post a Comment