Statistical Analysis of Circuit Timing Using Majorization

Future miniaturization of silicon transistors following Moore’s Law may be in jeopardy as it becomes harder to precisely define the behavior and shape of nanoscale transistors. One fundamental challenge is overcoming the variability in key integrated circuit parameters. In this paper, we discuss the development of electronic design automation tools that predict the impact of process variability on circuit behavior, with particular emphasis on verifying timing correctness. We present a new analytical technique for solving the central mathematical challenge of the statistical formulation of timing analysis which is the computation of the circuit delay distribution when delays of circuit elements are correlated. Our approach derives the bounds for the exact distribution using the theory of stochastic majorization. Across the benchmarks, the root-mean-square difference between the exact distribution and the bounds is 1.7–4.5% for the lower bound and 0.9–6.2% for the upper bound.

Back to Top

1. Introduction

A notable feature of silicon microelectronics at the nanometer scale is the increasing variability of key parameters affecting the performance of integrated circuits. This stems from the dramatic reduction in the size of transistors and on-chip wires, and is due to both technology-specific challenges and the fundamentals of nanoscale electronics. For example, one technology-specific challenge is the lack of a cost-effective replacement for using 193 nm light during the lithographic process, which yields poor fidelity when patterning transistors with a 20 nm length.

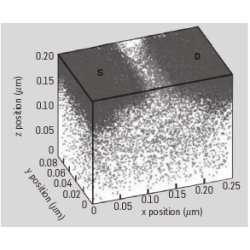
The more fundamental challenge is overcoming intrinsic randomness when manipulating materials on atomic scale. This randomness is, for example, manifested in threshold voltage variation, roughness of the transistor gate edge, and variation in the thickness of the dielectric transistor layer.² For example, the threshold voltage separating the on and off states of the transistor is controlled by adding dopant (non-silicon) atoms inside the transistor. Placing dopant atoms into a silicon crystal (see Figure 1) is essentially a random process, hence the number and location of atoms that end up in the channel of each transistor is likewise random. This leads to significant variation in the threshold voltage and many of the key electrical properties of the transistor.

Process parameters can be distinguished by the spatial scales on which they cause variability to appear, such as wafer-to-wafer, inter-chip, and intra-chip variability. Historically, intra-chip variability has been small but has grown due to the impact of technology-specific challenges in photolithography and wire fabrication, as well as the increased intrinsic randomness described above. Another important distinction is systematic versus random variability patterns. Systematic variation patterns are due to well-understood physical behaviors and thus can be modeled for a given chip layout and process. For example, the proximity of transistors to each other leads to a strong systematic effect on their gate lengths. Random variation sources, such as threshold voltage variation due to dopants, can only be described through stochastic modeling.

The variability in semiconductor process parameters translates to circuit-level uncertainty in timing performance and power consumption. The timing uncertainty is added to the uncertainty from the operating environment of circuit components, such as their temperature and supply voltage. The two sources of uncertainty, however, must be treated differently during the design process. Because a manufactured chip must operate properly under all operating conditions, environmental uncertainty is dealt with by using worst-case methods. The timing uncertainty due to process parameter variation can be dealt with statistically, since a small fraction of chips are allowed to fail their timing requirements and discarded during manufacturing.

Increased process variability presents challenges to IC design flows based on deterministic circuit analysis and optimization. This deficiency ultimately leads to a lower manufacturing yield and decreased circuit robustness, and results in designs that are sub-optimal in terms of silicon area or power consumption. A new design strategy is needed to seamlessly describe these variations and provide chip designers with accurate performance and robustness metrics.

Back to Top

2. Background

Validating the correctness of timing behavior is a paramount task of design flow. For large digital systems, this is performed using static timing analysis (STA). In contrast to dynamic timing simulations which trace circuit response for specific inputs, static timing analysis ensures correct timing of synchronous digital circuits in an input-independent manner.⁵

Virtually all current digital computing systems (such as microprocessors) are synchronous: all events are coordinated by a clock signal. A synchronous circuit is timing-correct if the signal computed by the combinational circuit is captured at the memory element, e.g., a flip-flop, on every latching edge of the clock signal (see Figure 2). The signal must arrive at the destination flip-flop by the time the latching clock edge arrives. The arrival time at the destination flip-flop is given by the path with the longest delay through the combinational circuit. Note that the clock signal arrival times vary from one memory element to another, and a complete timing analysis involves a simultaneous treatment of clock and data networks.

To carry out the timing checks, the circuit is represented by a graph with a vertex for each gate input/output and for the primary circuit inputs/outputs. A directed edge connects two vertices if the signal transition on the former causes a signal transition on the latter. Thus, the graph contains an edge for a transition between each possible input and output of the gate and for every interconnect segment. A virtual source node connected to all primary inputs is added to the graph, along with a virtual sink node connected to all primary outputs.

Definition: A timing graph G = {V, E, n_s, n_f} is a directed graph having exactly one source node n_s and one sink node n_f, where V is a set of vertices and E is a set of edges. The weight associated with an edge corresponds to either the gate delay or interconnect delay.

An example of a simple circuit and its timing graph is shown in Figure 3. The timing graph is, or can be made, acyclic, thus the final data structure is a directed acyclic graph (DAG). The basic job of static timing analysis is to determine the maximum delay between the source and the sink node of the timing graph; this is the focus of the present article. STA is effective because it relies on algorithms with runtimes that grow only linearly with circuit size. For DAGs, computing the maximum propagation time can be performed using a graph traversal following a topological order completed in O(|V| + |E|) time, where |V| and |E| denote the numbers of vertices and edges in the timing graph. In this method, the maximum arrival time to a given node is recorded and propagated, where the arrival time is the maximum time to propagate to a node through any path.

Traditional STA deals with the variability of process parameters deterministically by using the worst- and best-case corner strategy, in which edge delays are set to their maximum or minimum timing values that are possible as a result of process variation. This strategy fails for several reasons. First, corner-based deterministic STA produces increasingly conservative timing estimates, since it assumes that all edges behave in a correlated manner. This is reasonable only in the absence of intra-chip variability, which actually increases with scaling.¹³ Furthermore, the probability of simultaneously having the process values corresponding to the corners shrinks with the growing dimensionality of the process space. Second, the computational cost of running a corner-based deterministic analysis becomes prohibitive since the number of corner cases to be checked grows exponentially with the number of varying process parameters. Third, because it is difficult to properly identify the corner conditions in the presence of intra-chip variation, deterministic timing analysis cannot always guarantee conservative results.

Back to Top

3. Related Work

To overcome the limitations of deterministic timing, statistical static timing analysis (SSTA) has been proposed as an alternate way to accurately estimate circuit delay. SSTA models gate and interconnect delays as random rather than deterministic values and relies on fully probabilistic approaches to handle timing variability.

Definition: A timing graph G in which the ith edge weight d_i is random is called a probabilistic timing graph. A path p_i is a set of edges from the source node to the sink node in G. The delay of the path D_i is the sum of the weights d for all edges on the path. The goal of SSTA is to find the distribution of maximum (D₁, …, D_N) among all N paths in G.

Using a statistical treatment for STA requires an efficient method for processing probabilistic timing graphs with an arbitrary correlation of edge delays to find the distribution of maximum propagation time through the graph. This challenge has received significant attention by the electronic design automation (EDA) community.^{1, 3, 8, 9, 17, 18}

Edge delay distribution depends on the distribution of the underlying semiconductor process parameters, which is typically assumed to be Gaussian. A linear dependence of edge delays on process parameters is also commonly accepted. Under this model, edge delays also have a Gaussian distribution. They are correlated because of the simultaneous effect of intra-chip and inter-chip variability patterns. While intra-chip variability impacts individual transistors and wires in an uncorrelated manner, inter-chip variability causes all edges of the timing graph to vary in a statistically correlated manner. Probabilistic timing graphs have been studied by the operations research community in the context of PERT (program evaluation and review technique) networks.¹⁵ Earlier work, however, was largely concerned with the analysis of graphs with independent edge delay distributions. Even in this case, the exact distribution of graph propagation times cannot be generally obtained because arrival times become correlated due to shared propagation history.

The problem addressed by the EDA community is different in several respects: edge delays are correlated, estimating manufacturing yield requires capturing the entire cumulative distribution function (cdf) of duration time and not just the moments, and the network size is much larger (often with millions of nodes). Recent work in EDA has fallen into three categories: Monte-Carlo simulation,^{6, 9} numerical integration methods in process parameters space,⁸ and analytical techniques operating in edge delays space.^{3, 17, 18} Monte-Carlo approaches estimate the distribution by repeatedly evaluating the deterministic STA algorithm, with delay values sampled from their distributions. These algorithms tend to be computationally expensive since thousands of runs may be needed to achieve reasonable accuracy. While being accurate, numerical integration methods have prohibitively high runtimes which limits them to only a very small number of independent process parameters.

It is not feasible to analytically compute the exact circuit delay distribution under correlated edge delays even under simple correlation structures.¹² This has led to solutions that either approximate^{3, 17} or bound^{1, 18} the distribution. Approximations are typically used in the so-called node-based methods that involve approximation of the node arrival time distributions. This allows for statistical timing evaluation in a way similar to the traditional topological longest path algorithm, in which each node and edge of a timing graph is explored in a topological order and is visited once in a single traversal of the graph.^{3, 17} It thus preserves the linear runtime complexity of deterministic STA.

The computation of the node arrival time requires adding edge delays and then taking the maximum of edge delays. For two Gaussian variables, the sum is also Gaussian but the maximum Z = max(A, B) is not. Because node-based algorithms propagate arrival times through the timing graph, the edge delays and arrival times must be represented in an invariant manner when applying multiple add and max operators. The solution proposed in Jacobs et al.⁷ is to approximate the result of the max computation at each node by a new Gaussian random variable. This is based on matching the first two moments of the exact distribution of Z with a new normal random variable. The method is efficient because the mean and variance of the maximum of two normal random variables can be computed in closed form.⁴ In a timing graph with correlated edge delays, the new random variable must also reflect the degree of correlation it has with any other edge. For the known correlation between delay of edges A, B, and D, the correlation between max(A, B) and D can be computed in closed form.⁴ Instead of storing the full correlation matrix directly, a linear model of delay as an explicit function of process parameters can be used to capture the correlation.³

If each edge in the graph adds some independent random variation to the total delay, then capturing arrival time correlation due to common path history requires storing information on every traversed edge. The can become overwhelming, however, because the number of edges may be quite large. A solution proposed in Chang and Sapatnekar³ uses a dimensionality reduction technique of principal component analysis (PCA). If random components of delay contributed by timing edges belonging to the same region of the chip behave in a spatially correlated manner, then PCA is effective in reducing the number of terms to be propagated. An alternative strategy proposed in Visweswariah et al.¹⁷ is to lump the contributions of all random variation into a single delay term and represent the node arrival times and edge delays as

where P_i is the ith inter-chip variation component, ΔP_i = P_i − P_o is its deviation from the mean value, a_i is the sensitivity of the gate or wire delay to the parameter P_i, ΔR_a is a standard normal variable, and the a_n+1 coefficient represents the magnitude of the lumped random intra-chip component of delay variation. Representing random delay variation in this manner clearly cannot capture the correlation of arrival times due to signal paths sharing common ancestor edges. Yet keeping the path history makes the node-based algorithms less efficient, and known industrial applications¹⁷ tend to ignore the impact of path reconvergence by relying on the simple delay model shown above.

For Gaussian process parameter variations, the linearized delay models described above permit efficient add and max operations and propagate the result in the same functional form. For the max operation, the result is mapped onto the canonical model using a linear approximation of the form MAX(A, B) C = T_AA + (1 − T_A)B, where T_A = P(A > B) is known as the tightness probability.

Back to Top

4. Statistical STA Using Bounds

When computing the distribution of circuit delays, the quality of approximation degrades when applied to paths of equal criticality. In this case, the tightness probability is close to 0.5 and the linear approximation of the max operator becomes inaccurate, as illustrated below. As an example, in a perfectly balanced tree with 128 paths we have a node-based algorithm predicting a timing yield of 90% but the actual yield might be only 72% at some circuit delay values.

We propose a more reliable statistical estimation strategy using timing analysis that looks at a complete or large set of paths through the timing graph. The algorithm derives bounds on the circuit delay distribution using the distributions of path delays and their interdependencies.¹⁸ While path tracing imposes an additional cost, it also makes it easier to handle more complex gate delay models, for example, to accurately model the delay dependency on the slope of the driving signal. Delay correlations introduced by path-sharing and joint impact of inter-chip and intra-chip variations are naturally taken into account, improving the overall accuracy.

The major difference between this algorithm and node-based methods is the focus on bounding rather than approximating the circuit distribution; this avoids the multiple approximations involved in node-based traversal. Experiments indicate that produced bounds are quite tight. We are specifically interested in the lower bound on the cdf of circuit delay since it provides a conservative value of the circuit delay at any confidence level. For example, across the benchmarks the error between the exact distribution and the lower bound is 1.1–3.3% (95th percentile).

The cost of this greater accuracy is longer runtimes. In the worst case, the number of paths in the circuit increases exponentially with the number of nodes. This can occur in arithmetic circuits, such as multipliers, but the number of paths for most practical circuits is actually quite manageable. A study of a class of large industrial circuits found the number of paths 0.12 × gates^{1.42 14} The availability of parallel multi-core systems makes storing and manipulating millions of paths practical. Recent industrial offerings of transistor-level static timing analysis, where the accuracy requirement is higher than for the gate-level analysis, have used path-based analysis and demonstrated fast high-capacity multithreaded implementations.¹¹

Our algorithm separates the path extraction step from the statistical analysis of path delay distributions. It first extracts a set of the top N longest paths using deterministic STA. This is done using edge delays set to their mean values to extract paths with delays within a certain pre-defined range from the maximum delay. Path extraction can be done with time complexity of O(N), which means only paths larger than a given threshold need to be traced.¹⁹

The result of the path extraction step is a set of N paths with their mean delay values μ_Di, variances , and the path correlation matrix (Σ). The algorithm aims to find the distribution of the maximum delay of this set of paths. The complete description of a set of path delays is given by the cdf of D: F(t) = P(∩^N_i=1{D_i≤t}), where D_i is the delay of the ith path in the circuit and F(t) is the cumulative distribution function defined over the circuit delay probability space. The overall worst-case complexity of the algorithm is set by the path delay correlation matrix generation and is O(N²m²), where N is the number of paths extracted and m is the maximum number of gates on the extracted paths.

The main contribution of our work is an algorithm that computes the upper and lower bounds on the probability distribution of circuit delays for a timing graph with correlated random edge delays. The algorithm uses a linear model of edge delays as a function of process parameters. We assume that process parameters are Gaussian, and under the above linear model, the edge delays are also Gaussian. The algorithm is based on a set of transformations that bound the circuit delay distribution by probabilities in the form of equicoordinate vectors with well-structured correlation matrices; these probabilities can be numerically precharacterized in an efficient manner.

 4.1. Bounding the delay distribution

First, we express F(t) in terms of the distribution of a standard multivariate normal vector:

THEOREM 1. For any normal random vector with a correlation matrix given by Σ

where t’_i = (t − μ_Di)/σ_Di and Z_i ~ N(0, 1) are the standard normal random variables.

The transformation introduces the vector t’ that determines the set over which the probability content is being evaluated. Note that the components of the vector are not equal. Also note that the correlation matrix Σ that characterizes the path delay vector is populated arbitrarily and has no special structure. Both of these factors make the immediate numerical evaluation of the above probability impossible.

Second, we express the cumulative probability of Theorem 1 by a probability computed for a vector with a well-structured correlation matrix. We utilize a property unique to multivariate Gaussian distributions: their probabilities are monotonic with respect to the correlation matrix. Slepian has shown that by increasing the correlation between the members of the Gaussian vector, their probability volume over certain sets increases.¹⁶ Formally:

THEOREM 2. Let X be distributed as N(0, Σ), where Σ is a correlation matrix. Let R = (ρ_ij) and T = (τ_ij) be two positive semi-definite correlation matrices. If ρ_ij ≥ τ_ij holds for all i, j, then for all a = (a₁, …, a_N)^T, we have

It is easy to see that, as a special case, the above relation can be used to bound the sought probability with probabilities whose correlation matrices have identical off-diagonal components. Therefore, as a special case, the cumulative probability can be bounded from below and above by

where Σ_min (and Σ_max) are generated by setting all their off-diagonal elements to Σ^ij_min = min {Σ^ij} (and Σ^ij_max = max {Σ^ij}) for all i ≠ j. The bounding probabilities are thereby expressed in terms of simple and regular correlation matrices.

We now use majorization theory to evaluate the probability content of a standard multi-normal vector with a simple correlation structure over the non-equicoordinate set. For a more efficient numerical evaluation, we can resort to expressions in terms of the equicoordinate probability. This is attractive because it is easier to pre-characterize the probability of a multidimensional vector over a multidimensional semi-infinite cube rather than for all possible shapes of the multidimensional rectangular cuboid. We enable this transformation by bounding the cumulative probabilities of a normal random vector using the theory of stochastic majorization.¹⁰ We use the property that for some distributions, including Gaussian, stochastic inequalities can be established based on partial ordering of their distribution parameter vectors using ordinary (deterministic) majorization.

We first introduce the notions of strong and weak majorization for real vectors. The components of a real vector a = (a₁, …, a_N)’ can be arranged in increasing magnitude, a_[1] ≥ … ≥ a_[N]. A majorization relationship is defined between two real vectors, a and b. We say that a majorizes b, in symbols a b, if and for r = 1,…, N−1. If only the second condition is satisfied, then only weak majorization holds. We say that a weakly majorizes b, in symbols a b, if for r = 1,…, N. An example of strong majorization is (3,2,1) (2,2,2), and an example of weak majorization is (3,2,1) (1,1,1).

We now relate ordering of parameter vectors to ordering of probabilities. Note that the class of random vectors that can be ordered via ordering of their parameter vectors includes Gaussian random vectors. Specifically:

THEOREM 3. If = (t₁,…, t_N) and , where then

which establishes an upper bound on the circuit delay probability. We use weak majorization for the lower bound. Specifically:

THEOREM 4. If = (t₁, …, t_N), t_min = min (t₁,…, t_N) and = (t_min,…, t_min), then

Thus we have bounded the original probability by cumulative probabilities expressed in terms of the standard multivariate normal vector with an equicoordinate vector and a correlation matrix of identical off-diagonal elements:

This is a well-structured object whose probability content can be computed numerically. The numerical evaluation is done at pre-characterization time by Monte-Carlo integration of the cumulative distribution function of a multivariate normal vector. The result of pre-characterization is a set of probability lookup tables for a range of vector dimensionalities N, coordinate values t, and correlation coefficients.

We tested the algorithm on multiple benchmark circuits and compared our results to the exact cdf computed via Monte-Carlo runs of the deterministic STA algorithm. Samples were taken from the parameter distributions, and both inter-chip and intra-chip components were present.

Figure 4 shows the cumulative probabilities from the Monte-Carlo simulation and the derived bounds for one combinational benchmark circuit (c7552) containing 3874 nodes. The bounds are tight: across the benchmarks, the root-mean-square difference between the exact distribution and the bounds is 1.7–4.5% for the lower bound and 0.9–6.2% for the upper bound. Figure 5 illustrates that accurately accounting for edge delay correlations is crucial when predicting the shape of the cdf. The edge delay correlation changes with the ratio of the variance of inter-chip to intra-chip components. For example, the span of the low-correlation case is smaller than the high-correlation case. Our algorithm is more accurate than node-based approximation methods when processing balanced timing graphs with equal path mean delays and delay variances. In Figure 6, we compare the cumulative distribution functions generated by the node-based algorithm using the procedure of Visweswariah et al.¹⁷ against the proposed approach. The cdfs are generated for a balanced tree circuit with depth of 8. An equal breakdown of total variation into inter-chip and intra-chip variability terms was used. Note that the approximate cdf may be noticeably different from the true one, but the bounds accurately contain the true cdf.

The implementation is very efficient even though the algorithm runtime is quadratic in the number of deterministically longest paths. The C++ implementation ran on a single-core machine with a 3.0 GHz CPU and 1 GB memory and took less than 4 seconds for the largest circuit in the ISCAS ’85 benchmark suite (3874 nodes). When evaluated at a fixed number of extracted paths, there is a close-to-linear growth in algorithm runtime as a function of circuit size.

Back to Top

5. Conclusion

We have presented a new statistical timing analysis algorithm for digital integrated circuits. Instead of approximating the cdf of a circuit, we use majorization theory to compute a tight bound for the delay cdf. The equicoordinate random vectors are used to bound the exact cumulative distribution function, which facilitates the numerical evaluation of the probability.

Back to Top

Acknowledgments

We thank Ashish K. Singh for his help with the simulations, and Sachin Sapatnekar for his feedback on the article. The work has been partially supported by the NSF Career grant CCF-0347403.

Back to Top

Back to Top

Back to Top

Back to Top

Back to top