Formal Verification of Phase-Locked Loops Using Reachability Analysis and Continuization

We present a scalable and formal technique to verify locking time and stability for charge-pump phase-locked loops (PLLs). In contrast to the traditional simulation approach that only validates the PLL at a given operation condition, our proposed technique formally verified the PLL at all possible operation conditions. The dynamics of the PLL is described by a hybrid automaton, which incorporates the differential equations of the analog circuit elements as well as the switching logic of the digital circuit elements. Existing methods for computing reachable sets for hybrid automata cannot be used to verify the PLL model due to the large number of cycles required for locking. We develop a new method for computing effective overapproximations of the sets of states reached on each cycle by using uncertain parameters in a discrete-time model to represent the range of possible switching times, a technique we call continuization. Using this new method for reachability analysis, it is possible to verify locking specifications for a charge-pump PLL design for all possible initial states and parameter values in time comparable to the time required for a few simulation runs of the same behavioral model.

Back to Top

1. Introduction

In the standard design flow for analog mixed signal (AMS) circuits, the complete circuit is decomposed into its principal elements or blocks, which are first analyzed and designed using idealized low-order behavioral models. Detailed circuit-level designs are implemented only after the performance specifications have been verified at the block level over the required range of parameter variations and operating conditions. The goal is to create robust designs to avoid costly redesign cycles in the downstream process.

Because of the complexity of the mixed continuous and discrete (i.e., hybrid) AMS dynamics, there are no analytical techniques to verify a given design satisfies the circuit specifications, even for the simplified block-level behavioral models. Thus, numerical simulation has been the standard tool for evaluating the performance of behavioral models. Simulation is not completely satisfactory, however, because each simulation run represents the behavior for only one set of values for the initial states and parameters, so many simulations are required to assess the robustness of the design. Moreover, some specifications can be verified only after simulations have run for very long durations, and some specifications such as stability cannot be confirmed with absolute certainty because simulations cannot be run indefinitely.

This paper demonstrates an alternative to simulation based on formal methods. Formal methods offer an attractive alternative to simulation because they can verify that specifications for a circuit are satisfied for all possible behaviors over entire ranges of initial states and parameter values. This corresponds to an infinite number of simulation runs of unbounded duration. In their survey of the literature on formal verification for AMS designs, Zaki et al. categorize the methods into equivalence checking, automated state-space exploration, run-time verification, and proof-based methods.¹¹ Reachability analysis, the technique developed in this paper, is a form of automated state-space exploration.

The basic idea of reachability analysis is to use the dynamic equations for the circuit to propagate the trajectories of entire sets of states over time, rather than just a single state trajectory. The key issues are how to represent sets of states numerically and how to propagate these sets efficiently. Good techniques have been developed to represent and compute reachable sets for continuous dynamic systems (see e.g. Althoff ¹ and Girard et al.⁸). All of these techniques are based on overapproximations, since the actual sets of reachable states are not convex in general. These overapproximations become less accurate as time progresses, however, and for hybrid dynamic systems the overapproximations become even less accurate and more time consuming to compute due to the need to compute overapproximations of intersections of reachable sets with the surfaces representing switching conditions.^{2, 6} Therefore, current reachability analysis techniques for hybrid systems are effective when there are only a few discrete transitions in the time interval of interest.

To demonstrate the applicability of formal methods and reachability analysis to AMS circuits, we consider the verification of block-level behavioral models for a class of phase-locked loops (PLLs). PLLs are integrated circuits that produce high-frequency output signals that are synchronized to and in phase with low-frequency reference signals. Originally developed in the 1930’s as a circuit for radio receivers, millions of PLLs are now used in virtually all digital communication systems, from satellites to mobile phones, as well as in many other applications such as clock generation for microprocessors. The charge-pump PLL is one of the popular PLL architectures.⁷ It is an AMS circuit: the error signal driving the analog feedback is generated by digital logic.⁷

The primary requirements to be verified for a PLL are the circuit’s locking time and stability. These specifications are illustrated in Figure 1. Locking time is a transient specification: the PLL state must reach the invariant region within a specified number of cycles. Stability is an invariant specification: from some set of initial states, the magnitude of the phase difference must remain within a given bound indefinitely. Both of these specifications must be achieved robustly, that is, from an arbitrary initial state and over a range of parameter values that reflect the target operating conditions (e.g., a given temperature range) as well as the inherent uncertainties that will arise from the detailed design and manufacturing processes. Verifying the behavioral model of a PLL using simulation is time consuming and ultimately inconclusive because: (i) locking can take a few thousand cycles, so very long simulation runs are required; (ii) each simulation run represents the behavior for only one set of values for the initial states and parameters, so many simulations are required to assess the robustness of the design; and (iii) invariance can only be inferred, but not guaranteed, because simulations cannot be run indefinitely.

We present a method for verifying both the transient and invariant specifications for a PLL over entire ranges of initial states and parameter values using reachable set computations that can be performed in the same amount of time currently required to simulate the circuit models for just a few selected points in the design space. Our approach relies on some new techniques tailored to the PLL problem because locking can require thousands of cycles, which implies there will be thousands of discrete transitions in the switching logic. Experiments with existing methods implemented in tools such as PHAVer⁵ or SpaceEx⁶ show that the overapproximations using existing methods become inaccurate so quickly that it is impossible to demonstrate that locking occurs, even for simple cases where locking can be demonstrated analytically.

The main technical contribution of this paper is a new method for computing accurate overapproximations of reachable sets for hybrid systems when there are a large number of discrete state transitions. This approach leverages previous results on computing reachable sets for linear systems with bounded uncertain parameters. Using the equations that govern the continuous dynamics of the PLL, we create a discrete-time model that generates tight overapproximations of the reachable sets at the beginning of each continuous-time cycle. Since the actual times at which the discrete transitions occur can vary, we introduce bounded uncertain parameters in the linear discrete-time model that account for the variations in the actual transition times. We call this process of mapping variations in time into parameter uncertainties continuizaton.³ Finally, we show that satisfaction of the PLL specifications for the discrete-time model guarantees the specifications are satisfied at all points in time. The reachable sets for the discrete time model can be computed very fast, and the time reduced further by taking advantage of certain symmetries in the PLL dynamics. Our approach illustrates how the successful use of formal methods to solve real problems often requires extensions and insights that exploit the particular structure and features of the target application. It is an enabling technique that facilitates us to efficiently verify a PLL at all possible operation conditions.

We begin in the next section by showing how a class of charge-pump PLLs can be modeled at the behavioral level using hybrid automata with uncertain parameters. Section 3 presents a conversion of the continuous-time behavioral model to a discrete-time model, which provides the solution of the original model after each cycle. Variations in switching times of the PLL are abstracted away in Section 4 using the new concept of continuization. This makes it possible to abstract the hybrid dynamics of the PLL by a linear system with uncertain parameters. Using the model resulting from continuization, Section 5 presents the application of reachability analysis for formal verification of the PLL specifications, and Section 6 presents a comparison of the verification results using reachability to the classical simulation approach. The concluding section summarizes the contributions of this paper.

Back to Top

2. PLL Behavioral Model

We consider the dual path, type II, third-order charge-pump PLL shown in Figure 2, consisting of a reference signal generator (Ref), a voltage-controlled oscillator (VCO), a phase frequency detector (PFD), and charge pumps (CPs), along with RC circuits to implement a PI controller for the feedback loop. The reference frequency generator produces a sinusoidal signal at a fixed low frequency (MHz), and the VCO generates a high-frequency signal (GHz). The desired output frequency of the VCO is determined by the reference frequency and the frequency divider ratio (i.e., N). The purpose of the PLL is to ‘lock’ the controlled frequency of the VCO so that its output has the same frequency (when divided by N) and phase as the reference signal.

Locking of the PLL is achieved by the PFD by comparing the phases of the reference signal and the VCO signal and setting the signals UP = 1 if the reference signal leads, and DN = 1 if it lags. These signals pump charge into or out of the capacitors, changing voltages v_p and v_i, which serve as proportional and integral (PI) control inputs to the VCO. For instance, if the reference signal leads, it means that the reference signal is faster than the VCO signal (when divided by N). In this case, UP is set to 1 and the “up” current will charge the capacitors so that the voltage values v_i and v_p increase. As a result, the VCO frequency increases in order to catch the reference signal. We do not consider adaptation of PLL parameters such as the frequency divider, resistor, or capacitor values.

As one can see from Figure 2, different components of the PLL system operate at different frequencies. For instance, the reference signal is at low frequency, while the VCO signal may be at extremely high frequency if the frequency divider ratio N is large. The large difference in frequency makes PLL simulation extremely challenging, since a traditional simulation tool must adopt a very small time step to numerically solve the PLL response in time domain. It, in turn, results in a very long simulation time.

The behavioral model of the charge-pump PLL is a hybrid automaton⁴ with linear continuous dynamics and uncertain parameters. Appropriate bounds on the uncertain parameters can be determined by equivalence checking with detailed circuit models.^{9, 10} These bounds should be chosen to assure that the behavioral model represents all possible behaviors of a detailed circuit model. If the more detailed model is at the transistor level, the approach is also able to catch issues at the transistor level. However, current equivalence checking techniques are typically semi-formal such that a complete enclosure cannot yet be guaranteed.

The continuous state vector in the behavioral model is x = [v_i v_p1 v_p Φ_v Φ_ref]^T with input vector u = [i_i i_p]^T (see Figure 2). The dynamics are

with

where the resistor and capacitor values are given in Figure 2 and the values K_i, K_p, and f₀ determine the frequency of the VCO: . Input values u vary depending on the signals leaving the PFD according to

The output signals of the PFD are determined by threshold crossings of phase signals. The switching logic is described by the automaton shown in Figure 3, where the states are labeled as up_active, dn_active, both_active, and both_off.

Starting in both_off, the next discrete state of the hybrid automaton is up_active if the reference signal leads by first reaching Φ_ref = 2π, and dn_active when Φ_v = 2π is reached first. As shown in Figure 4, in order to use the same phase crossings for the next cycle, the phase values are reset to Φ_ref:=Φ_ref – 2π, Φ_v:= Φ_v – 2π upon continuing in up_active and dn_active. Once the lagging signal has a zero-crossing, the discrete state both_active is entered which models a time delay t_d for switching off both charge pumps. After the delay, the system is in both_off again, which completes one cycle. Locking is achieved when the phase difference reaches and remains within the locked condition given by the interval [–0.1°, 0.1°].

Back to Top

3. Time Discretization

Given the hybrid automaton behavioral model of the PLL, we first derive a discrete-time linear model with bounded uncertain parameters based on the phase of the reference signal, assuming the reference signal leads the VCO signal, that is, for the discrete state sequence up_active → both_active → both_off. The time for a cycle of the reference signal is given by t_cycle = 1/f_ref. Since the continuous dynamics of the PLL is linear, we can take advantage of the superposition principle and obtain the initial state solution and the input solution separately. The initial state solution for one cycle is given by . The input solution for constant input u over the time interval [0, r], where r is the time the charge pump is active, can be written using the Taylor series of e^At as

where ⊕ = {a + b|a ∈ , b ∈ } is a Minkowski addition and ⊗ = {ab|a ∈ , b ∈ } a set-based multiplication. Note that sets can be sets of scalars, vectors, or matrices, and sets may also contain just a single (certain) element. The set multiplication sign is sometimes dropped when the context makes it clear that uncertain matrices are involved. The standard operator precedence rules apply. The set of remainders ε^p(r) is overapproximated by an interval matrix, that is, a matrix with lower and upper bounds on each element, as presented in Althoff et al.³ Since there is no input for the rest of the cycle, the input solution after one cycle is . Let t_on denote the time the system is in location up_active and recall that t_d is the time it is in both_active. Also, let u denote the input in up_active and u_d denote the input in both_active. Finally, defining x_k = x(k t_cycle), the combination of the initial state solution and all input solutions can be written as

The above formula is a discrete-time overapproximation of the continuous-time evolution after one cycle.

Back to Top

4. Continuization

The model derived above computes the state of the system after one cycle when the switching time of the charge pumps is known. In this section, we develop a model that computes the range of state values that can occur at each cycle, for the entire range of possible switching times t_on (while t_d is a given constant). A closed form solution does not exist for t_on, which depends on the state of the system. Simulation techniques obtain t_on by detecting a zero-crossing which corresponds to crossing the guard condition Φ_v == 0. Here we propose a more efficient method based on overapproximating the interval of possible values for t_on. Since t_on depends only on Φ_v = x₄, it is sufficient to consider (see (1))

We assume user-defined bounds which are monitored during the verification process. Violation of these bounds would require to restart the verification with larger intervals. Applying interval arithmetic to (4) results in the bound . We further extract the bound on x₄ from the reachable set at the beginning of each cycle. We obtain using the fact that the reference signal is leading , resulting in

Using bounds on the switching times derived above, we use the concept of continuization to compute the set of reachable states resulting from uncertain switching times. To compute the reachable set under uncertain switching times (see Figure 5), we modify (3) and compute the solution successively, first of _k at times t_k + _on, then of _k+1 at times t_k+1. This makes it possible to reset the uncertain switching time to values in the interval [0, Δt_on], Δt_on = _on − Δ _on compared to [ _on, _on], which has computational benefits when evaluating Taylor series since higher order terms can be tightly bounded. The new equations are:

We drop the cycle index k for the following deviations for simplicity. It is possible to extract the time from the set (Δt_on), to obtain the relatively tight inclusion

where (Δt_on) is an interval matrix derived in Althoff et al.³ Combining this result with using the idea in (5) yields

Now, the expression in (6) is written in terms of , independent of the current mode. Thereto, we use the fact that u only changes sign between modes based on the phase difference, which is taken care of by redefining the input u: = sgn(x₄(t_k))(–u). We also consider that u ∈ , where is an interval vector, such that

where 0 represents zero vectors of proper dimension and Θ(Δt_on) is an interval matrix.

The result of (7) holds no matter if the phase difference is positive or negative as long as the time interval [ _on, _on] is correctly overapproximated. The time intervals computed in (5) are based on the cycle including up_active. If the cycle containing dn_active is also considered, the bounds are

When computing the state bounds for a constant cycle time t_cycle, the input is applied in the interval t_k + [0, t_on] for the cycle containing up_active and in the interval t_k – [0, t_on] for the cycle containing dn_active. As shown in Algorithm 1 below, the different times are taken care of by adding the reachable set due to the input before and after t_k when both cycles are possible. The addition of the input solution for t_k + [0, t_on] and t_k – [0, t_on] results in an overapproximation since the input solution contains the origin, so that the previous sets are contained in the set after the addition. Further, it is sufficient to only keep the input applied at t_k + [0, t_on] for subsequent computations, which is illustrated in Figure 6. Thus, the error for adding the input solution for t_k + [0, t_on] and t_k – [0, t_on] does not accumulate. The procedure of only keeping the input applied at t_k + [0, t_on] is realized by the auxiliary reachable set _k in Algorithm 1. We skip the proof that this procedure is overapproximative due to space limitations.

Back to Top

5. Reachability Analysis

We now present how to compute the reachable set for a set of initial states and a sequence of cycles. The reachable sets are represented using zonotopes which have a maximum complexity of (n³) with respect to the system dimension n for the required operations. A zonotope is defined as

where c ∈ ⁿ is the zonotope center (to which a zonotope is centrally symmetric) and the g⁽ⁱ⁾ ∈ ⁿ are called generators. The order of a zonotope is defined as . Figure 7 illustrates a zonotope being constructed step-by-step as the Minkowski sum of a finite set of line segments _i = [–1, 1] g⁽ⁱ⁾. Operations on zonotopes and operations between sets of matrices and zonotopes are presented in Althoff.¹

 5.1. Transient analysis

The algorithm for the reachable set computation when the reference signal is initially leading is presented in Algorithm 1. An interesting property of the PLL is that the number of cycles required for locking is identical when the absolute value of the initial phase difference is equal and the corresponding initial voltages are symmetric with respect to the voltages in the completely locked state. We refer to this property as symmetric locking time which makes it sufficient to compute the reachable set only for the case when the reference signal is initially leading. For the symmetric locking, we additionally require that and , which can be relaxed for reachability analysis by choosing the intervals for and large enough such that their center is 0. The proof for symmetric locking is omitted due to space limitations.

For simulation purposes, the values of the phases Φ_ref and Φ_v are needed to determine the time for turning the charge pumps on and off. In contrast, the discrete-time model for reachability analysis does not require the exact timing for switching the charge pump values; it is sufficient to keep only the phase difference x₄:= Φ_v – Φ_ref as a state variable and remove x₅ for the reachability computations.

 5.2. Invariant computation

Once the reachable set fulfills the locking condition |P _k| ≤ ΔΦ_lock (see Algorithm 1), it remains to check if this condition is fulfilled indefinitely. A straightforward procedure would be to check after each cycle if _k+1 ⊆ _k, meaning that _k is an invariant. Checking _k+1 ⊆ _k is computationally expensive. This is because zonotopes have to be represented by polytopes and the enclosure check for polytopes is computationally expensive.¹

For this reason, we use the following alternative procedure illustrated in Figure 8. First, the reachable set computations are continued for extra cycles after a reachable set fulfills the locking condition in cycle k_lock, see Figure 8. Next, the reachable set is overapproximated by an axis-aligned box denoted by . This leads to an overapproximation for the subsequent reachable sets, so should be chosen large enough such that all the subsequent sets fulfill the locking condition. Once a reachable set represented by a zonotope is enclosed by (which is computationally cheap to detect), one can conclude that the PLL is locked indefinitely.

Back to Top

6. Numerical Results

We apply Algorithm 1 and the invariant computation to verify a 27 GHz PLL designed in 32 nm CMOS SOI technology. Note that the PLL was designed in a commercial process at an advanced technology node. Hence, it provides a practical example to demonstrate the efficacy of our proposed verification method. The parameters of the PLL and the reachable set computation are listed in Table 1. The PLL considered here employs a simple initialization circuitry that sets the integral and proportional path voltages to common-mode levels at power up and whenever the division ratio is changed. This reduces locking time and aids the formal verification by reducing the uncertainty on the initial node voltages. With the initialization, the initial range of node voltages are v_i(0) ∈ [0.34, 0.36], and v_p1 (0), v_p(0) ∈ [–0.01, 0.01]. We normalize the phases to [0, 1], and we normalize the time to microseconds. The phase range of Φ_v is split into 5 subintervals , where i = 1 … 5, and without loss of generality we assume Φ_ref (0) = 0. Because of symmetry, all possible initial phase differences are considered. The number of Taylor terms chosen depends on the time horizon. For Γ(t_cycle − _on), 30 Taylor terms are used and 10 Taylor terms are used for all other computations. The aforementioned experiment setup allows us to formally verify the PLL with consideration of initial voltage and phase uncertainties. Note that these uncertainties cannot be efficiently incorporated into the traditional simulation approach, as a traditional simulation can only validate the PLL with a specific initial condition.

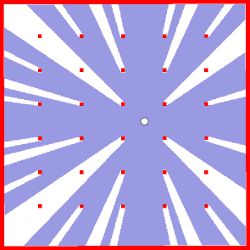
The reachable set starting with the initial phase difference (0) is shown for the first 200 cycles in Figure 9 for projections onto four different pairs of state variables. The sets computed to prove locking are shown in Figure 8. In this example, the proposed verification algorithm is able to prove that independent of the initial condition, the PLL reliably locks to the reference signal. Note that the voltages in Figure 9 are as high as 10 [V] since charge pump saturation is not yet considered. It is possible to further extend our verification method to consider charge pump saturation by applying a nonlinear behavior model.

Table 2 shows the clock cycles it takes for the PLL to achieve locking for varying initial phase errors. The 1st and the 2nd columns show the results from reachability analysis. The 3rd column shows the maximum lock time obtained from 30 behavioral simulations with randomly varying initial phase errors and charge pump currents. We use the maximum lock time since the verification task is to check if the PLL always locks before a specified locking time, that is, we are investigating the worst-case behavior. Note that we are not providing any stochastic evaluation since this is not the focus of this work. Table 2 demonstrates that our reachability analysis efficiently provides an upper bound on the worst-case lock time in the presence of random phase error and charge pump current variations. On the other hand, it is important to note that the traditional approach based on Monte Carlo simulation cannot guarantee to find the “true” maximum lock time. Unless an infinite number of Monte Carlo runs are performed, the maximum lock time may not be captured by one of the Monte Carlo runs.

The computation times for the reachability analysis starting at different initial sets of phase differences are listed in Table 3. It can be seen that the results are obtained in less than a minute. The average computation time of the reachability analysis for a single cycle is around 27 [ms], which is only slightly longer than 24 [ms] required for a simulation of one cycle of the behavior model in MATLAB. All computations mentioned so far have been performed on an Intel i7 processor with 1.6 GHz and 6 GB memory. Simulating the behavioral model in VerilogA for a particular initial condition requires only 2 [ms] per cycle on an Intel Xeon CPU with 2.53 GHz, which is an order of magnitude faster than reachability analysis. However, reachability analysis is still competitive if we consider that the VerilogA model needs to be simulated for thousands of Monte Carlo samples to capture random initial conditions and parameter variations.

Back to Top

7. Conclusion

This paper presented a method for verifying PLL locking using efficient reachability analysis. Efficient reachability computations are achieved using a discrete-time linear model with uncertain parameters and continuization to eliminate the complexity of switching. In contrast to applying a classical reachability approach, the intersection of guard sets can be dropped. As a consequence, the only operations on sets that remain, can be performed using zonotopes, which have a maximum complexity of (n³) with respect to the system dimension n. The verification of locking does not require any Lyapunov function to show convergence. For future work, we plan to consider saturations of charge pumps and varactor nonlinearities. We are also looking at other applications of continuization for hybrid systems where the transition time can be accurately overapproximated by a linear function of the state plus uncertainty. In addition to PLL, the proposed reachability analysis may be further extended to verify the circuit functionality and performance specifications of other AMS systems in time domain.

Back to Top

Acknowledgments

The authors acknowledge the support of the NSF Award CCF0926181 and the C2S2 Focus Center, one of six research centers funded under the Focus Center Research Program (FCRP), a Semiconductor Research Corporation entity.

Back to Top

Back to Top

Back to Top

Back to Top

Back to Top

Back to top