A holy grail of theoretical computer science, with numerous fundamental implications to more applied areas of computing such as operations research and artificial intelligence, is the question of whether NP is equal to P. Much of modern technology is based on the so-called Cobham-Edmonds’ thesis (named after Alan Cobham and Jack Edmonds), which states that algorithmic problems can be feasibly computed on a computational device only if they can be computed in polynomial time. In a nutshell: P means “feasible” while NP-hard means “infeasible” to compute.
Moving from theory to practice, and looking at problems more realistically, the size of the exponent in a polynomial-time algorithm matters a lot. In the era of big data, when is, say, the number of users of Facebook or Twitter, an – or even -time algorithm might be too slow. In such applications where the input size is very large, any practically efficient algorithm that solves a problem to optimality can only afford a linear or almost linear-time complexity. While the distinction between computationally infeasible and feasible problems has classically been “NP-hard vs. polynomial-time solvable,” in the big data era it becomes “polynomial-time vs. (quasi-) linear-time solvable.”
Parameterized algorithmics for polynomial problems. When a fast algorithm (polynomial) is not fast enough (that is, not linear) and when plausible relative lower bounds speak against further speedups for important algorithmic problems, what can one do?a For NP-hard (traditionally computationally infeasible) problems, there are several established coping strategies, including heuristics (fingers crossed that a worst case does not appear), approximation (polynomial-time algorithms that provide approximate instead of optimal solutions), and parameterized algorithmics (be fast if the input instance carries a small parameter value); see Roughgarden36 for an overview. With the advent of big data it has become apparent that we do not only face speed issues for NP-hard problems, but also for problems solvable in polynomial time. For instance, the classic Cocke-Younger-Kasami algorithm for parsing context-free languages is not used in practice due to its cubic running time, thus resorting to constrained context-free languages and corresponding linear-time parsing algorithms such as LL- and LR-parsing. Indeed, with the recent advent of fine-grained complexity analysis,10,38 we have clear indications that some of our beloved polynomial-time algorithms cannot be further improved without implying unlikely consequences in computational complexity theory. Prominent examples in this direction include all-pairs shortest paths,39 Fréchet distance,9 and longest common subsequence in strings.11
Two recent trends in theoretical computer science toward addressing this challenge are again approximation algorithms and parameterized algorithms. For instance, Duan and Pettie16 developed a linear-time algorithm for computing near-maximum weight matchings. Iwata et al.26 developed an -timeb exactc parameterized algorithm for computing maximum-weight matchings, where is the treewidth of the given graph. Notably, while no quasi-linear-time algorithm is known to compute maximum-weight matchings in the general case, the mentioned algorithms achieve such a running time in relaxed settings (approximate solutions or input graphs with small parameter values). In what follows, we want to review and discuss possibilities of a parameterized view on bypassing established complexity barriers for polynomial-time solvable problems. More specifically, we focus on the power of (linear-time) parameterized preprocessing in combination with a rigorous mathematical analysis, which may guide algorithm design. To this end, we present, illustrate, and discuss three basic concepts of parameterized preprocessing in the context of polynomial-time solvable problems.
Three directions of parameterized preprocessing. Our focus is on decreasing the algorithmic complexity by processing the input without giving up the possibility to find an optimal solution for the problem for any input instance. That is, we exclude approximation algorithms or considerations in the direction of approximation-preserving preprocessing. We identify and delineate three fundamental approaches for parameterized preprocessing which helped to gain significant (practical) improvements in algorithmic performance over previously existing approaches. The basic common aspects of these three preprocessing variants are, on the one hand, their focus on high efficiency of preprocessing (typically linear time) and, on the other hand, their use of appropriate problem-specific parameters (that is, some numbers measuring specific, algorithmically crucial, features of the input) to obtain an overall efficient algorithm with mathematically provable performance guarantees. With the vision of systematizing and unifying existing ideas and approaches, we use in the remainder of our article illustrative examples from graph algorithmics to delve deeper into the following three fundamental directions of parameterized preprocessing. In the following, we abstain from a discussion of the art of problem parameterization—while some parameterizations are more or less obvious, others (including guarantee parameterization or distance-from-triviality parameterization) leave quite some room for creative explorations.34,35
Parameterized size reduction. This approach originally stems from parameterized algorithmics for NP-hard problems and is known as kernelization. The point here is to efficiently preprocess the input by trying to identify and remove unnecessary or nonmeaningful parts, thus hopefully shrinking the input size considerably. To this end, one replaces the input instance by an “equivalent” one whose size can be upper bounded by a hopefully small function of the chosen parameter only. In this way, one may obtain a rigorous way of provably effective preprocessing. Moreover, this is a pretty universal approach in the sense that the resulting reduced instance, also known as “(problem) kernel,” can be typically attacked with any known solving strategy (such as exact, approximation, or heuristic algorithms). We exemplify this preprocessing approach in the context of computing a maximum-cardinality matching in undirected graphs, using the parameter feedback edge number of the graph.
Parameterized structure simplification. This approach is perhaps the most natural alternative to kernelization: instead of shrinking the size of the input, simplify its structure. That is, we replace the original input with an equivalent one having a simpler structure, which we can then algorithmically exploit. Here “simpler” typically means that, apart from some few bad substructures, the rest of the input has nice properties that allow for an efficient algorithm to be applied. The fewer these bad substructures in this simplified (but equivalent) instance, the more efficient this algorithm will be. The chosen parameter comes naturally into play: we demand the number of bad substructures in the simplified instance (which is the only cause of inefficiency) to be upper bounded by a function of the parameter only. We exemplify the structure simplification approach in the context of computing longest paths in interval graphs, using a very natural parameter.
Parameterized data structure design. This approach is sort of closest to classic approaches of preprocessing and has been extensively used for query-based problems. The scenario is that we have an input on which many queries are expected to be asked later. The approach here is to first design and implement an auxiliary data structure by preprocessing the given fixed input, and then to have an algorithm that quickly answers each query by operating exclusively on this auxiliary data structure. Here, the parameter comes into play in a more subtle way by measuring favorable properties of the data structure. We exemplify this preprocessing strategy in the context of computing shortest paths in edge-weighted, undirected graphs, using the parameter treewidth which measures how close an input graph is to being a tree.
Here, we discuss these three directions in more detail.
Parameterized Size Reduction (Kernelization)
It is fair to say the method of kernelization is the practically most relevant method developed in parameterized algorithmics for NP-hard problems.17 Here, we want to advocate kernelization in the context of polynomial-time solvable problems, an issue that has been rarely touched so far but opens several theoretically and practically promising research and application avenues.
Recall that a kernelization algorithm is a preprocessing algorithm that applies a set of data reduction rules to reduce a large problem instance to an equivalent smaller instance—a so-called kernel. We call an instance resulting from the application of a data reduction rule a reduced instance. The kernel can be seen as the final reduced instance, in which no data reduction rule can be applied any more. On this kernel, one can use any known exact, approximation, or heuristic algorithm to solve the problem. Recently, data reduction rules received a lot of attention in practice as well.21,24
Data reduction rules are evaluated in terms of correctness, efficiency, and effectiveness. A data reduction rule is correct if any optimal solution of the reduced instance can be extended to an optimal solution of the original input instance. Correctness is a necessary requirement for all data reduction rules used in kernelization. It is efficient if it can be applied much faster than the algorithm solving the problem instance, while it is effective if the size of the kernel is smaller than the original instance size. While correctness and efficiency are analyzed for each data reduction rule separately, the effectiveness is analyzed in the context of (typically) exhaustively applying all data reduction rules.
Our key illustrating example here is Maximum-Cardinality Matching: Given an undirected graph , the task is to find a maximum matching, that is, a maximum-cardinality edge subset such that no two edges in share an endpoint. The (theoretically) fastest algorithm for this problem runs in time (see Blum6 and the discussion therein).
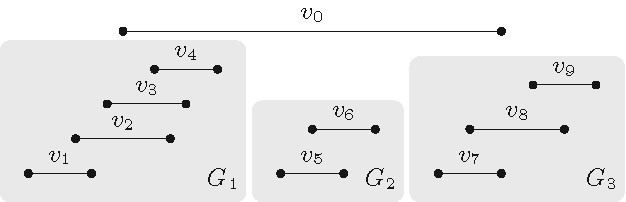
The kernelization algorithm we consider for Maximum-Cardinality Matching consists of two simple data reduction rules already considered by Karp and Sipser in the early 1980s.27 The first rule removes degree-one vertices from the input graph (see also Figure 1):
Data Reduction Rule 1. Let be a degree-one vertex with neighbor . Then select the edge for the maximum matching and delete and .
First, let us convince ourselves that the data reduction rule is correct. A maximum matching for the initial graph can have at most one more edge than a maximum matching for the reduced graph . Given a maximum matching for , we can construct a matching for . Thus, is a maximum matching.
Second, as to efficiency, it is straightforward to implement the rule so that it can be exhaustively applied in linear time.
As mentioned, the effectiveness shall be analyzed in combination with the second data reduction rule that removes degree-two vertices from the input graph. To this end, folding a degree-two vertex means to delete and its two neighbors and introduce a new vertex adjacent to all vertices at distance two from (see Figure 2).
Data Reduction Rule 2. Let be a degree-two vertex. Then fold .
The idea is as follows: In a maximum matching we can always match with either or . Which of these two cases applies is not easy to decide in advance. However, if we have a matching where at least one of and is not matched, then the choice is trivial: match with (one of) the non-matched neighbors. In any case, since Data Reduction Rule 2 deletes both vertices and , it ensures at most one of the edges incident to and can be in a matching of the resulting graph. Exhaustively applying Data Reduction Rule 2 in linear time is non-trivial but doable.2
Now we analyze the effectiveness of the two data reduction rules, that is, the size of the final reduced instance after applying them exhaustively. To this end, we make use of the kernelization concept from the toolbox of parameterized algorithmics and, to keep things simple, we only consider a very basic and typically large parameter: In the worst case, the graph does not have any degree-one or degree-two vertices and the reduction rules are not applicable. If, however, the graph is very tree-like in the beginning, namely, there are only a small number of edges to be removed such that the graph becomes a tree, then in the intermediate reduced instances there will be many degree-one and/or degree-two vertices and, thus, the number of vertices in the resulting kernel will be small. Next, we formalize the statement;33 herein, the feedback edge number denotes the minimum number of edges one must remove from a connected graph to obtain a tree. Exhaustively applying Data Reduction Rules 1 and 2 on graph produces a reduced graph such that:
The graph contains vertices, where is the feedback edge number of , and,
Given a maximum-cardinality matching for , one can compute in linear time a maximum-cardinality matching for .
The rough argument for the upper bound on the number of vertices of the resulting graph is as follows: The minimum vertex degree in is three. As none of the two reduction rules introduces new cycles, has still feedback edge number at most . Thus, removing edges results in a tree (or a forest) in which at most vertices of degree one and two exist. Since is a tree, it follows by a simple counting argument that it has at most vertices of degree at least three. Hence, contains at most vertices.
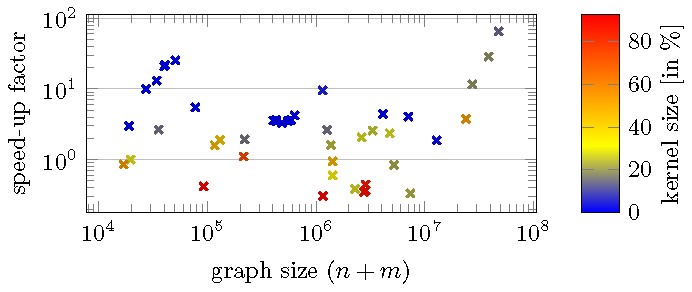
Besides this theoretical measure for the effectiveness of Data Reduction Rules 1 and 2, there is also strong experimental evidence:29 The probably still fastest practical algorithm, due to Kececioglu and Pecqueur,28 was tested on real-world graphs from the SNAP30 large network dataset collection with 104 to 108 edges, once with and once without exhaustively applying the two data reduction rules before running their algorithm. The effect of the preprocessing ranged from a slow down by a factor 3 to up to 60 times faster. On average the speed-up factor was 4.7 (see Figure 3 for some details).
These experimental results reflect the theoretical prediction as follows: For “bad” instances (all of these have high parameter value) the data reduction rules do not reduce the input size by much; however, since these rules are relatively easy, it does not take much time to apply them. In contrast, for “good” instances (with small parameter value) where most of the graph is reduced by the rules, the overall algorithmic speed-up is pronounced. As the subsequent algorithm that we apply to the kernel has usually a nonlinear running time, the exhaustive application of the data reduction rules in linear time basically comes for free in terms of the overall algorithmic complexity, for both good and bad instances. Notably, for our example, Kececioglu and Pecqueur28 state a worst-case running time of for their algorithm, where is the inverse of Ackermann’s function. This is worse than the theoretically best bound of ,6 but in practice Kececioglu and Pecqueur’s algorithm is still state of the art. Altogether, we conclude that even moderately shrinking the input has a significant impact on the running time.
To summarize, the simple kernelization algorithm can significantly improve even a sophisticated matching implementation on real-world graphs with many low-degree vertices. Of course, reduction rules are used for many further problems, including linear programs or SAT solvers.5,23 Data reduction rules that can be exhaustively applied in time linear in the input size of the original instance are particularly attractive: even if there is no effect on the input instance, then there is no large penalty in the overall running time of solving the problem at hand.
Overall, kernelization is a very universal and flexible approach interesting for theory and practice: the parameterized framework allows us to get theoretical guarantees that yield good predictions on the efficiency and effectiveness of data reduction rules in practice.
Parameterized Structure Simplification
To gain fast algorithms, a key approach is to exploit some specific structural property of the input. However, in practice, the input often does not directly have such a special property that we can use, which makes this approach often not applicable in real-life scenarios. Indeed, detecting such useful properties can be an algorithmic challenge on its own. The idea we put forward here is like the kernelization approach in that we also rely on exhaustively applying the rules that modify the input instance. The difference is that, using a problem-specific parameterization, we simplify the structure of the input instead of shrinking its size; thus, we call these rules data simplification rules. Once this preprocessing phase is done, we can then use another algorithm which is efficient on inputs having the desired special property. In this algorithmic scheme, the preprocessing approach helps to constrain the search space (using a function of the parameter) for a subsequent algorithm, thus leading to overall faster algorithms in the case of small parameter values.
Our key illustrating example for the structure simplification approach is Longest Path on Interval Graphs: Given an undirected interval graph , the task is to find a longest path, that is, a path in whose length is as large as possible; if every vertex of additionally has a positive weight assigned to it, then the task becomes to compute a path having the largest total weight on its vertices. Since this is a fundamental NP-hard problem on general graphs, which directly generalizes the famous Hamiltonian Path problem, researchers have tried to identify “islands of tractability,” that is, appropriate graph families such that, for every graph with vertices, a longest path in can be computed in time that is polynomial in . One of the well-known graph families for which this is possible is the class of interval graphs, where a longest path can be computed by a dynamic programming algorithm with running time .25 Although this running time is polynomial, the degree of the polynomial is too high for being practical when the number of vertices becomes large; however, to date this remains the fastest known algorithm for the problem. We will see that some acceleration can be achieved if the interval graph is close to the special case of being a proper interval graph.
A graph is an interval graph if one can assign to every vertex exactly one closed interval on the real line such that is adjacent to if and only if (see Figure 4a). If such a collection of intervals exists such that none of them is properly included in another one, then is called a proper interval graph (see Figure 4b). Interval graphs have received a lot of algorithmic attention due to their applicability in DNA physical mapping, genetics, molecular biology, and scheduling problems.19,20
By closely analyzing -time dynamic programming algorithm,25 it turns out a very slight refinement of it runs in time whenever in the input interval graph has at least vertices that are independent, that is, pairwise non-adjacent; that is, if the intervals associated with these vertices are pairwise nonintersecting.18 In such a case, we say the parameter vertex cover number of the graph is upper-bounded by (see Figure 5): the vertex cover number of a graph is the size of the smallest vertex subset such that every edge is incident with at least one vertex of . We can conclude the following:
Fact 1. For an interval graph with vertex cover number , a longest path in can be computed in time.
Moreover, the same refined algorithm correctly computes a longest path of , even if has positive weights on its vertices. It is worth noting here that, since we always have that , the running time becomes in the worst case, and thus it is asymptotically tight with respect to the currently best-known algorithm for general interval graphs.
The main idea for our illustrating example of structure simplification lies in the fact that, after appropriately preprocessing the input interval graph (which has a potentially very large vertex cover number, for example, , we compute a new graph with small vertex cover number; then we can apply the -time algorithm to to compute a longest path in both and , as we will describe. That is, the desired “special property” after the preprocessing phase is having small vertex cover number.
The pre-processing uses the fact that a longest path in a proper interval graph can be trivially computed in linear time. Indeed, due to the monotone arrangement of the intervals, every connected proper interval graph has a Hamiltonian path, that is, a path that traverses each vertex exactly once.4 Such a Hamiltonian path can be found by traversing all intervals from left to right, and thus a longest path of a proper interval graph can be computed by just finding its largest connected component.
Fact 2. For a proper interval graph with vertices, a longest path in can be computed in time.
Consequently, although interval and proper interval graphs are superficially similar, they appear to behave very differently when trying to compute a longest path in them.
What makes it substantially more difficult to compute a longest path in an interval graph? The intuition for this is illustrated by a simple example in Figure 6. In this figure the only source of complication comes from the fact there is one long interval and we must decide which of the smaller subgraphs (each of them being proper interval) will connect their Hamiltonian paths using as a connector interval. The situation becomes even more complicated when we have more long intervals and more proper interval subgraphs, all of which can be interconnected in many different ways. The fastest known way to deal with such cases is to recursively check the appropriate points where these connector intervals (that is, the long ones) connect the parts of the various proper interval subgraphs to combine them appropriately to build a longest path.
This discussion naturally leads to the appropriate parameter that measures the backdoor40 or distance to triviality22 for the problem Longest Path on Interval Graphs: the size of a minimum proper interval (vertex) deletion set, that is, the minimum number of vertices that we have to delete from an interval graph to obtain a proper interval graph.18 As it turns out, given an interval graph , a proper interval deletion set of size at most can be computed in linear time by appropriately traversing the intervals from left to right.18
Based on this distance-to-triviality parameter, Giannopoulou et al.18 provided a polynomial-fixed parameter algorithm for interval graphs that computes a longest path in time, implying linear time for constant values of . In summary, the main idea of this algorithm is as follows:
Exhaustively apply two data simplification rules in total time to obtain an interval graph (with appropriate vertex weights) that has vertex cover size .
Apply to the algorithm behind Fact 1 with running time to compute a longest path of , and thus at the same time also a longest path of .
The details of the two data simplification rules of this preprocessing phase are quite delicate; therefore, we focus here on highlighting the main ideas behind them. The first simplification rule deals with specific sequences of intervals of that have the all-or-none property; that is, a longest path contains either all intervals of the sequence or none of them; note this property generalizes the idea behind Fact 2. In each of these sequences, the intervals form a proper interval subgraph. Once we have identified these sequences, we replace each one of them with one single interval having an integer weight equal to the number of intervals of the sequence. The important structural property of these new weighted intervals is they are mutually non-intersecting (that is, they are independent), and thus they cannot be connected to each other directly in any path (see Figure 7 for a visualization). That is, in contrast to the kernelization approach, here by exhaustively applying this first simplification rule we do not upper-bound the number of these new intervals (in fact, there can be many), but we simplify their structure instead. Moreover, as these new intervals are mutually non-intersecting, all other intervals form a vertex cover of the graph, see Figure 5.
The second data simplification rule proceeds as follows. The (at most) intervals of the proper interval deletion set (which we have already computed in linear time) divide the real line into at most disjoint parts. For each of the pairs of these disjoint parts of , we consider the intervals of the graph that have their left endpoint in the one part and their right endpoint in the other one. As it turns out, we can just replace all of these (potentially many) intervals with few new intervals (in fact, many), each of them having an appropriate positive weight. Thus, we have in total new weighted intervals after exhaustively applying the second simplification rule. This in turn implies the vertex cover of the resulting (weighted) interval graph is . Thus, we can now apply the refined dynamic-programming algorithm, obtaining overall an algorithm that computes a longest path of the input interval graph in time in total.
In summary, structure simplification is a natural “sister approach” to kernelization in the sense of focusing on creating nice structure instead of merely shrinking size in the reduced instance. Both however, make decisive use of appropriate problem-specific parameters (with hopefully instance-specific small values) to perform a rigorous mathematical analysis providing theoretical (worst-case) guarantees. As to structure simplification, we also point to the concept of treewidth reduction used in the context of NP-hard problems;32 treewidth will also be a key concept in the main illustrating example for the third direction of parameterized preprocessing.
Parameterized Data Structure Design
A classic approach to faster algorithms is to first build up appropriate clever data structures, and then to design algorithms that exploit these data structures to solve the target problem. Correspondingly, fundamental data structures such as heaps are discussed in every basic textbook on algorithms and usually have very well understood guarantees. Our goal here is to exhibit a strategy based on classic pre-processing (that is, by first building up a helpful data structure) in conjunction with a parameterized analysis of the computational complexity.
Our key illustrating example here is the computation of shortest paths, known to be solvable in time using Dijkstra’s classic algorithm. This running time is fast, however, sometimes not fast enough when used in modern applications such as real-time route planning, where is huge (for example, all cities in the U.S.). We describe an approach that efficiently computes shortest-path queries using tree decompositions—a data structure originating from algorithmic graph theory frequently used in parameterized algorithmics to cope with NP-hard problems. The approach to be described will not provide good worst-case guarantees in general; however, a parameterized analysis using treewidth,1,12 combined with the fact that many infrastructure networks have small treewidth,31 shows its benefits. Indeed, the described ideas are used in practice on quite large datasets, for example in Microsoft’s Bing Maps.3,14
In our setting, the input graph is a static, edge-weighted graph representing, for example, a road network. The task is to quickly report the distance—the length of a shortest path—between different pairs of vertices. To this end, we will compile , that is, we build in a preprocessing step a data structure on which the subsequent algorithm can quickly answer distance queries between any pair of vertices of . We remark that the approach allows for queries reporting the shortest path and fast weight updates without compiling repeatedly.3,4
We first present three simple facts that are exploited in the approach. Then, we give a high-level description of the concepts of tree-decomposition and treewidth. Finally, we explain how the overall approach works.
First, assume the input graph is a tree. Then, computing the distance between and boils down to finding the lowest common ancestor of and . Consequently, the following holds:
Fact 3. In a tree of height , the distance between and can be computed in time.
Second, simply computing the distance between all possible pairs of vertices in the graph and storing the results in a table of size yields the following:
Fact 4. Using a size- table, one can answer every distance query in constant time.
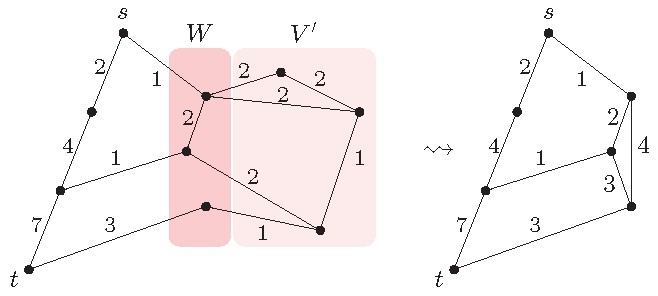
The table size of , however, is prohibitively large for real-world applications. This leads us to our next and last fact. Assume there is a vertex subset in the graph such that:
is connected to the rest of the graph via a small separatord and
contains neither nor (see left side in Figure 8).
We can simplify the graph as shown in Figure 8 (right side). Our goal is to delete from . Since a shortest path might pass through , however, we need to keep the information about all possible paths through . To encode this information, we use that every sub-path of a shortest path is also a shortest path and combine this with Fact 4: Compute all pairwise distances for vertices in the separator within the induced graph . and store the obtained distances using weighted edges with both endpoints in , see Figure 8 (left side). After that, one can remove without changing any distance between the vertices .
Fact 5. Let separate from with . Then remove and add edges representing shortest paths within as displayed in Figure 8.
We now combine Facts 3 to 5 into an algorithmic strategy. Note that the usefulness of a separator (in Fact 5) depends on and . Moreover, our data structure shall support very fast distance queries for all pairs . But which separators should be used in the preprocessing (before and are known)? Considering all separators is clearly too expensive because there can be exponentially many of those. Instead, we need a relatively small set of not-too-large separators. A tree-decomposition provides such a set (given that the input graph has small treewidth).
A tree-decomposition of a graph is a tree containing . More precisely, each bage of contains a vertex subset of and, in particular, the following conditions are fulfilled (see Figure 9 for an example):
Every vertex of appears in at least one bag of .
For any two bags that are adjacent in , the intersection of their vertex sets is a separator in .
The treewidth of a graph is if there exists a tree-decomposition such that each of the (at most bags in contains at most vertices (thus the separators are small).
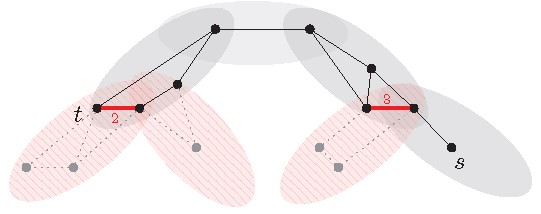
Now the algorithm for answering -distance queries by using a (properly preprocessed) tree-decomposition and Facts 3 to 5 works as follows:
Find two bags containing and , respectively.
Find the shortest path between these two bags in the tree (see gray bags in Figure 10).
Take the graph induced by the vertices in the bags of . Based on Facts 4 and 5, add to the weighted edges encoding all paths in that go via bags not in (see thick red edges in Figure 10).
Compute and return an -distance in using Dijkstra’s algorithm.
An extension of the preprocessing allows to return not only the distance but also a shortest path between and . The algorithm here requires a tree-decomposition, which can be computed once in the preprocessing. Computing an optimal tree-decomposition is NP-hard. However, there are practically useful heuristics computing tree-decompositions.13,37 Moreover, any tree-decomposition can be transformed efficiently into another tree-decomposition with depth and roughly three times larger bags.7 This ensures the path found in Step 2 is of length .
For the computation of in Step 3, one needs the precomputed distances in the separators. More precisely, for each pair of adjacent bags one must compute for all vertex pairs in the pairwise distances in both subgraphs that got disconnected by the separator. For each pair of bags, these pairwise distances will be stored in tables to allow constant-time access. Overall, these computations can be done using dynamic programming in time,1 where is the treewidth of the graph.
Next, we analyze the running time of this algorithm. Since the depth of is , it follows that the path contains bags and can, by Fact 3, be found in time. By definition of treewidth, contains vertices and edges. Thus, using Dijkstra’s algorithm in requires time to obtain the distance between and . For moderately small , this is a sub-linear running time. In infrastructure networks the treewidth is typically .31 Hence, in such networks the query time is usually .
Overall, the parameterized analysis yields a very good theoretical explanation and predictor for the practically observed efficiency. To the best of our knowledge, there are only few examples of similar data-structure-driven preprocessing algorithms combined with a parameterized analysis. One of these is given by a study with Gomory-Hu trees to compute minimum cuts.8
Notably, the presented preprocessing approach only works in conjunction with the algorithm answering the shortest path queries with the tree-decomposition. This is like structure simplification but in stark contrast to kernelization, which can be used as a preprocessing step before exact, approximate, or heuristic algorithms. We mention in passing, however, that the shortest path setting discussed here seems to be resistant to kernelization as any vertex in the graph can be the start or the end vertex of a query.
Summary and Outlook
Parameterization enjoyed great success in refining the computational complexity analysis of NP-hard problems, leading to an extremely rich area with a wealth of results and techniques. In this article, we wanted to steer the view also to the area of polynomial-time solvable problems. More specifically, we focused on parameterized preprocessing, highlighting the potential of parameterized algorithm design for speeding up slow polynomial-time algorithms. The overall message we offer here is that looking through parameterized glasses, one may find promising avenues toward (provably) accelerating algorithms for fundamental computational problems.
Our studies are closely linked to the somewhat more general framework of studying fixed-parameter tractability for polynomial-time solvable problems18 and the fine-grained complexity analysis framework.38 The latter offers, based on assumptions such as the Exponential Time Hypothesis, fresh ideas for proving the worst-case optimality of several known polynomial-time algorithms. Notably, parameterization again may break these fine-grained barriers by adding new dimensions of analysis, that is, problem-specific parameters that help to further refine the analysis and to design parameterized and multivariate algorithms.
Already in their path-breaking textbook on parameterized complexity in 1999, Downey and Fellows15 complained about the lack of predictive power of classic computational complexity analysis (and, correspondingly, algorithm design). Their parameterized complexity ideas enabled new views on the (worst-case) computational complexity landscape of mostly NP-hard problems. Taking up their ideas and trying to make them work in the world of polynomial-time problems is promising; indeed, in the era of big data, polynomial time frequently is just not enough to represent efficiency. Parameterized (quasi-)linear-time preprocessing, as we discussed, might contribute to remedying this situation.
Acknowledgments
We dedicate this work to the memory of our dear colleague, friend, and mentor Rolf Niedermeier, who passed away unexpectedly during the revision process of this article.
We are grateful to two CACM reviewers for constructive feedback that helped to significantly improve our presentation. The research was supported by the DFG project FPTinP, NI 369/16, and by the EPSRC grant EP/P020372/1.





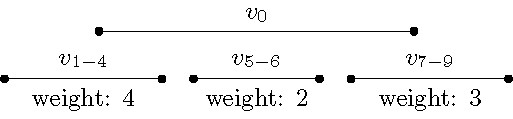



Join the Discussion (0)
Become a Member or Sign In to Post a Comment