Changing an object’s shape is a basic operation in computer graphics, necessary for transforming raster images, vector graphics, geometric models, and animated characters. The fastest approaches for such object deformation involve linearly blending a small number of given affine transformations, typically each associated with bones of an internal skeleton, vertices of an enclosing cage, or a collection of loose point handles. Unfortunately, linear blending schemes are not always easy to use because they may require manually painting influence weights or modeling closed polyhedral cages around the input object. Our goal is to make the design and control of deformations simpler by allowing the user to work freely with the most convenient combination of handle types. We develop linear blending weights that produce smooth and intuitive deformations for points, bones, and cages of arbitrary topology. Our weights, called bounded biharmonic weights, minimize the Laplacian energy subject to bound constraints. Doing so spreads the influences of the handles in a shape-aware and localized manner, even for objects with complex and concave boundaries. The variational weight optimization also makes it possible to customize the weights so that they preserve the shape of specified essential object features. We demonstrate successful use of our blending weights for real-time deformation of 2D and 3D shapes.
1. Introduction
Interactive deformation is the task of assisting the user to alter an object’s shape. In the case of 2D cartoon deformation, we could ask the user to manually reposition each pixel of the image, but this is unnecessarily tedious. The space of coherent configurations of the 2D shape is much smaller than the space of all possible positions for every pixel of the image. Hence, we would rather the user provide only a few, high-level constraints like “open the mouth,” “enlarge the belly,” or “bend the tail” (Figure 1). The rest of the shape should immediately deform in an intuitive manner. We may interface such high-level constraints to the user with handle structures, like skeletons composed of rigid bones, enclosing cages, and selected regions or points.
With these handles, interactive space deformation becomes a powerful approach for editing raster images, vector graphics, geometric models, and animated characters. This breadth of possibilities has led to an abundance of methods seeking to improve interactive deformation with real-time computation and intuitive use. Real-time performance is critical for both interactive design, where tasks require creative exploration, and interactive animation, where deformations need to be computed repeatedly, often sixty or more times per second. Among all deformation methods, linear blending and its variants dominate practical usage thanks to their speed: each point on the object is transformed by a weighted combination of a small number of affine transformations.
In a typical workflow, the user constructs a number of handles and the deformation system binds the object to these handles; this is termed bind time. The user then manipulates the handles (interactively or programmatically) and the system deforms the shape accordingly; this is pose time. Unfortunately, existing linear blending schemes are not always easy to use. The user must choose a particular handle type a priori, and different types have different advantages (Figure 2). Skeleton-based deformations offer natural control for rigid limbs, but are less convenient for flexible regions. Generalized barycentric coordinates improve volumetric or area control over classical lattice-based free-form deformations, but still require construction of closed or nearly closed cages that fully encapsulate transformed objects and can be tedious to manipulate. In contrast, variational techniques often support arbitrary handles at points or regions, but at a greater pose-time cost.
Real-time object deformations would be easier with support for all handle types above: points, skeletons, and cages. Points are quick to place and easy to manipulate. They specify local deformation properties (position, rotation, and scaling) that smoothly propagate onto nearby areas of the object. Bones make some directions stiffer than others. If a region between two points appears too supple, bones can transform it into a rigid limb. Cages allow influencing a significant portion of the object at once, making it easier to control bulging and thinning in regions of interest.
Our goal is to supply influence weights for a linear blending scheme that produce a smooth and intuitive deformation for handles of arbitrary topology (Figure 1). We desire real-time interaction for deforming high-resolution images and meshes. We want smooth deformation near points and other handles, so that they can be placed directly on animated surfaces and warped textures. And we seek a local support region for each handle to ensure that its influence dominates nearby regions and disappears in parts of the object controlled by other handles.
Our solution computes blending weights automatically by minimizing the Laplacian energy subject to upper and lower bound constraints. Because the related Euler–Lagrange equations are biharmonic, we call these weights bounded biharmonic weights and the resulting deformation bounded biharmonic blending. The weights are computed once at bind time. At pose time, points on the object are transformed in real time by blending a small number of affine transformations. Our examples demonstrate that bounded biharmonic blending produces smooth deformations, and that points, bones, and cages have intuitive local influences, even on objects with complex and concave boundaries. Our weight computation requires space discretization and optimization, which could be a drawback in some applications, but the generality of our formulation also makes it possible to provide additional control over the energy minimization, for example, to define weights that preserve the shape of specified essential object features.
2. Previous Work
Variational, or energy-minimizing, methods are known to compute high-quality shape-preserving deformations for arbitrary handles on the surface,4,6,9,22 and some variational methods work with bones25 or can be extended to other off-surface handles.5 The primary drawback of these techniques is that they rely on optimization at pose time. Although system matrices can be prefactored and back-substitution can be implemented on a GPU, it is not an embarrassingly parallel problem like linear blend skinning, and is therefore much slower. Even with significant performance tuning19 or model reduction,7,23 pose-time optimization is too slow to deform high-resolution objects at high frame rate, as necessary, for example, for video games.
Most methods that are fast at pose time compute the transformation of each point on the object by using a weighted blend of handle transformations. To perform the blending, some methods use moving least squares,16 some use dual quaternions,14 but most use linear blend skinning (LBS).15 With LBS, the affine transformations of the handles are linearly averaged with different weights to transform each vertex. Although linearly blending rotations leads to well-known artifacts, LBS has been a popular technique for skeletal animation for over two decades because it is simple, predictable, and the pose-time computation can be implemented very efficiently on a GPU. In addition to skeletal animation, most cage-based deformation methods8,12,13 are effectively LBS, where the handle (cage vertex) transformations are restricted to be translations and the focus is choosing the weights. Additionally, the reduced-model variational shape deformation methods mentioned above use LBS to go from the reduced model to the full model.
The choice of weights for LBS determines whether the affine transformations of the handles affect the shape intuitively. In some cases, weights that have a closed form in terms of the handle structure have been used,13,17 but more often they are precomputed at bind time or are painted by hand. In Section 3.1, we formulate the desirable properties of LBS weights, and in Section 3.2 we discuss previous weight choice schemes in the context of these properties.
3. Bounded Biharmonic Weights
Our goal is to define smooth deformations for 2D or 3D shapes by blending affine transformations at arbitrary handles. Let Ω ⊂ ℝ2 or ℝ3 denote the volumetric domain enclosed by the union of the given shape S and cage controls (if any). We denote the (disjoint) control handles by Hj ⊂ Ω, j = 1, …, m. A handle can be a single point, a region, a skeleton bone (such that Hj consists of all the points on the bone line segment), or a vertex of a cage. The user defines an affine transformation Tj for each handle Hj, and all points p ∈ Ω are deformed by their weighted combinations:
where wj: Ω → ℝ is the weight function associated with handle Hj. Note that cages are generally understood as closed polygons in 2D or polyhedra in 3D containing S or part of it, but our framework is agnostic to the cage topology and treats a cage simply as a collection of simplices, with the requirement that these simplices transform linearly as the cage vertices are translated. Hence, open cages are possible (Figure 3). We do not consider cage faces (line segments in 2D or triangles in 3D) as handles; they receive linear weights, as we will see in Section 3.1. Note also that for skeleton bones connected by joints, we formally include each joint point in one single bone of those that share it (we assume that the skeleton is never torn apart, i.e., that all bones sharing a joint transform the joint to the same location). In practice, we constrain the weights at shared points to be equally distributed between the overlapping bones to maximize the symmetry of our weights.
We propose to define the weights wj as minimizers of a higher-order shape-aware smoothness functional, namely, the Laplacian energy, subject to constraints that enforce interpolation of the handles and several other desirable properties:
where Fc is the set of all cage faces and δjk is Kronecker’s delta. Figure 4 shows an example of wj computed for point handles.
The following properties possessed by our weight functions wj allow for intuitive and high-quality deformations.
Smoothness: Lack of smoothness at the handles causes visible artifacts in 2D textured shapes (Figure 5) and prevents placing handles directly on 3D shapes. Note that by calculus of variations, minimizing the Laplacian energy (2) amounts to solving the Euler–Lagrange equations, which are the biharmonic PDEs in this case: Δ2wj = 0. Equivalently, we could formulate our blending weights as minimizers of the linearized thin-plate energy, as it leads to the same biharmonic PDE (see e.g., Botsch and Sorkine6). The bounded biharmonic weights are C1 at the handles and C∞ everywhere else, provided that the posed boundary conditions are smooth. This is always the case, with the exception of skeletal joints and cage vertices: for bones connected by joints, the weights must have a discontinuity at the joints since wj on bone Hj is 1 and it must be zero on the adjacent bone. However, this does not lead to smoothness problems for the actual deformations because the joints are always transformed to the same location by all emanating bones.
Explicit linear interpolation constraints (4) on cage faces are required to achieve expected behavior, since otherwise the cage faces would not deform linearly when translating cage vertices. These linear constraints on cage faces preclude smoothness of the weights at the cage vertices. Therefore, our deformations are not smooth at cage vertices, but they are smooth everywhere else, including across cage faces.
Nonnegativity: Negative weights lead to unintuitive handle influences, because regions of the shape with negative weights move in the opposite direction to the prescribed transformation. We explicitly enforce nonnegativity in (6), since otherwise biharmonic functions (as in Botsch and Kobbelt3) are often negative, even if all boundary conditions are nonnegative (right).
Shape awareness: Informally, shape awareness implies intuitive correspondence between the handles and the domain Ω. The influence of the handles should conform to the features of the shape and fall off with geodesic (as opposed to Euclidean) distance. The best shape-aware behavior one can hope for is when the weights wj depend on the metric of Ω alone and do not change for any possible embedding of Ω. Our weights are shape-aware since the bi-Laplacian operator is determined solely by the metric.
Partition of unity: This classical property (also seen in, e.g., Bézier or NURBS) ensures that if the same transformation T is applied to all handles, the entire object will be transformed by T. We enforce this property explicitly in (5) since nonnegative biharmonic weights do not sum to 1, unlike unconstrained biharmonic weights.
Locality and sparsity: Each handle should mainly control a shape feature in its vicinity, and each point in Ω should be influenced only by a few closest handles. Specifically, if every locally shortest path (in a shape-aware sense) from a point p to Hj passes near some other handle, then Hj is “occluded” from p and wj(p) should be zero. We observed this property of our weights in all our experiments.
No local maxima: Each wj should attain its global maximum (i.e., value of 1) on Hj and should have no other local maxima. This property provides monotonic decay of a handle’s influence and guarantees that no unexpected influences occur away from the handle. This property was experimentally observed in all our tests; likely, it is facilitated by imposing the bound constraints (6). Without these constraints, the biharmonic functions in general do not necessarily achieve maxima at the handles and cause deformation artifacts. While bounded biharmonic weights often do not have local extrema, it is certainly not the case that they are always monotonic.a In fact, local extrema invariably appear on shapes with long appendages geodesically equidistant from handles. Dealing with this non-monotonic behavior requires a dedicated optimization.11
3.2. Comparison to existing schemes
Existing schemes formulate and satisfy subsets of these properties, but not all. For example, Shepard’s17 and similar weights (used in embedded deformation23 and moving least squares image deformation16) are dense and not shape-aware. Cage-based schemes do not support arbitrary handles: for example, extending harmonic coordinates12 to handles in the cage interior results in a lack of smoothness (see Figure 5). Heat diffusion weights2 suffer from the same problem. Natural neighbor interpolation21 is one of the few schemes that guarantees locality, but it is also not smooth at handles. Biharmonic weights without constraints3 are smooth, but can be negative (or greater than one), have local maxima away from handles, and can result in nonlocal influences. Table 1 shows the properties satisfied by several methods.
A number of methods have most recently been focusing on locally preserving or prescribing angles.24 While they have elegant formulations in terms of complex analysis, these methods are, in general, restricted to 2D.
The energy minimization framework supports incorporating additional energy terms and constraints to customize the weight functions. One example of a useful addition is making all points of a specified region Π ⊂ Ω undergo the same transformation, that is, have all the weight functions be constant on Π (∇wj|Π = 0). Since typically we only prescribe translations, rotations, and uniform scales at handles, this implies that Π will undergo a similarity transformation in 2D and an affine transformation in 3D, so that the shape of Π will be preserved. Similarly to the rigidity brush in Igarashi et al.,9 the user can paint Π with a (possibly soft) brush, creating a mask ρ: Π → ℝ+; we then add a least-squares term to our energy minimization:
See Figure 6, where the shape-preservation brush helped retain the shape of the man’s eye while deforming the nose. Note that this is different from placing a handle because no explicit transformation needs to be prescribed by the user; the painted region transforms according to its weights.
We discretize our constrained variational problem (2) using linear finite elements in order to solve it numerically with quadratic programming (we use the flattened mixed finite element method (FEM) formulation for fourth-order problems, as discussed in Jacobson et al.10). Assuming that the object S is given as a 2D polyline or triangle mesh in 3D, we sample vertices on all provided skeleton bones and cage faces, and mesh the domain Ω in a way compatible with all of the handles and the vertices of S. The result is a triangle/tetrahedral mesh M whose vertices V = {v1, …, vn} include all discretized Hj‘s and the object itself. The weights become piecewise-linear functions whose vertex values we are seeking; we denote them by column vectors wj = (w1,j, w2,j, …, wn,j)T.
The Laplacian energy (2) is discretized using the standard linear FEM Laplacian M–1L where M is the lumped mass matrix (with Voronoi area/volume Mi of vertex vi on each diagonal entry i) and L is the symmetric stiffness matrix (i.e., the cotangent Laplacian):
We impose the constraints (3)–(6) using the discretized handles. To discretize the additional shape-preservation energy term (7), we employ the linear FEM gradient operator G (see its derivation in Botsch and Sorkine6). Gwj is a vector of stacked gradients, one gradient per element (triangle in 2D and tetrahedron in 3D; since we deal with linear elements, the gradient over an element is constant). Let R be a diagonal matrix containing the integrals of the user brush ρ over each element, and let
be the per-element mass matrix (i.e., for each triangle/tet i,
i contains its area/volume). Then the energy term in (7) is discretized as
Note that the matrix GT R
G is a kind of weighted linear FEM Laplacian, and therefore its sparsity pattern is a subset of the main energy matrix LM–1 L, creating no new non-zeros. Hence, adding this energy term does not increase the optimization complexity.
We use Triangle18 for 2D-constrained Delaunay meshing and TetGen20 for constrained tetrahedral meshing to create the discretized domains. In 2D, we configure Triangle to create triangles of near uniform size and shape. For all our 2D examples, Triangle takes less than a second, even for detailed images which require pixel-size triangles. In 3D, we configure TetGen to create rather graded tet meshes to reduce complexity (Figure 7); for the Armadillo mesh of 43,234 vertices and 120 vertices sampled internally along bones, the resulting tet mesh has 46,898 vertices. For the Armadillo and all our 3D examples, TetGen takes a few seconds.
The energy terms in (8) and (9) are quadratic in the unknowns wj and convex, and (3)–(6) are linear equality and inequality constraints. We use MOSEK1 as a sparse quadratic programming solver to compute the weights for all of the handles simultaneously.
Since the time necessary to solve the quadratic program is superlinear in the number of unknowns, dividing it into several smaller subproblems allows for a significant speedup. Notice that the optimization of each handle is independent of the rest if we drop the partition of unity constraint (5). We have implemented this strategy, solving for each wj separately and then normalizing the weights for each vertex in a postprocess. We have observed mostly negligible average differences between this faster solution and the original one, often resulting in visually indistinguishable deformations (Figure 8). Larger differences occasionally occur far from handles, but the weights have the same qualitative behavior: smoothness and observed local support. For the Gargoyle in Figure 9, for example, computing the weights for 7 handles separately is 50 times faster than computing them simultaneously. We report the timings as well as the difference between the original and these faster weights in Section 4.
Once the weights are computed, the deformation itself is real-time even for very large meshes, since it is computed with a GPU implementation of linear blend skinning (1).
In the cage-based systems of the various barycentric coordinate methods, the only inputs are the translations of the cage vertices. In our system, the user provides a full affine transformation at each handle. Depending on the application, the user may choose to specify only translations, that is, identity rotations and scales. However, nontrivial rotations are often necessary to achieve a desired effect, and these could be tedious to specify manually. We found it easier to have rotations inferred from the user-provided translations using run-time optimization in the reduced subspace of linear blend skinning with bounded biharmonic weights, similar in spirit to Der et al.7
4. Results
Bounded biharmonic blending combines intuitive interaction with real-time performance. Its controls unify three different interaction metaphors so that simple tasks remain simple and complex tasks become easier to achieve.
Experiments. Points are a particularly elegant metaphor for manipulating flexible objects.9 Although similar transformations could be accomplished with bones, the Octopus in Figure 10 and Worm in Figure 2 illustrate the simplicity of direct point manipulation of supple regions and highlight the inappropriateness of using rigid bones for the same task.
In contrast to previous techniques,9,12 our approach deforms shapes smoothly even when the handle transformations are large. Figure 5 illustrates the importance of smoothness to minimize texture tearing.
We have observed our weights to be local and free of spurious local maxima in all examples tested. Figure 11 compares the support regions of our weights to the biharmonic functions of Botsch and Kobbelt,3 which are globally supported and contain many local extrema.
Some tasks are more easily accomplished by controlling both points and lines. Figure 12 demonstrates our weights with smooth point-based warping while the external cage maintains or resizes the image boundary. Cages are ideally suited for precise area control. In Figure 3, we use an arbitrary collection of open and closed lines to manipulate the shape and orientation of the tower. These deformations and fine adjustments, needed to account for perspective distortions, are difficult to achieve with points or lines alone.
Our approach generalizes naturally to 3D. At bind time, the optimization distributes the weights over the volume so that linear blending delivers smooth deformation at run time. This scheme ensures real-time performance and low CPU utilization even for high-resolution meshes. We note that cages can be even more tedious to set up in 3D than in 2D, particularly when they are required to envelop objects fully. For tasks such as hand manipulation shown in Figure 13 (left), skeletons are easier to embed and use to manipulate a 3D object. Skeletons still suffer from joint-collapse problems and lack the precise volume control offered by cages, and our approach supports and simplifies the combined use of bones and cages. In particular, our approach supports partial cages that control parts of the object but are not required to surround it fully. Figure 13 (right) shows a simple cage used to enlarge the belly of the Mouse. As always, partial cages can be combined with points and bones, and this combined use of all three metaphors is often the most powerful.
Figure 7 shows combined use of points and skeletons. We create a sequence of poses of the Armadillo by embedding a human skeleton. The skeleton does not control the tail or the ears, so their deformations need to be adjusted. This is done most directly by attaching a few points. Direct surface manipulation makes it easy to bend the tail into a more realistic pose and expressively curl the ears. Likewise in Figure 9, point handles are a natural and simple choice of control for stretching and bending the wings of the Gargoyle. Bounded biharmonic weights combine the motion of the skeleton and configuration of these points to yield smooth deformations.
Discussion. We have tested our method on a MacPro Quad-Core Intel Xeon 2.66 GHz computer with 8 GB memory. The bind time measurements of our unoptimized code are reported in Table 2. One limitation of our solution is the optimization time needed to compute the weights at bind time. We discretized the problem using linear FEM, although other choices may be more efficient, such as the multiresolution framework used in, for example, Botsch et al.5 and Joshi et al.12 Generating bounded biharmonic weights in 3D requires a discretization of the volume. Note that once a volume is computed, an arbitrary embedded object (e.g., polygon soup) may be deformed without regard for its topology.
Our bounded biharmonic weights do not have the linear precision property, that is, they do not necessarily reproduce linear functions. This property is necessary for cage-based deformations (e.g., Joshi et al.12 and Ju et al.13) that apply the deformation solely by interpolating the positions of cage vertices, because otherwise, they would distort the shape when the cage is rotated. In contrast, our approach allows arbitrary transformations to be supplied at the handles and blends them over the shape; we therefore do not have to rely on linear precision to be able to work with rotations. A comparison for translational deformation between the linearly-precise harmonic coordinates12 and our cages is shown in Figure 14 with a rectangular image.
In this paper, we have only experimented with linear blending deformations based on (1); however, our weights are also useful with more advanced methods of transformation blending, such as dual quaternions.11,14
5. Conclusion
We have shown how to unify all popular types of control handles for intuitive design of real-time blending-based deformations. This allows users to freely choose the most convenient handles for every task and relieves them from the burden of manually painting blending weights.
In future work, we would like to optimize the efficiency of our bind-time precomputation. Aside from looking at alternative discretizations and numerical approaches, further analysis will help to reduce the dimensionality of the quadratic program: the observed locality property implies that the weights vanish on significant portions of the domain, which could thus be removed from the minimization.
Skinning-based deformations are prone to foldovers and self-intersections, as the deformation mapping is not always injective. Our method is no exception. Building a reduced model with our weights for simulation and contact handling is worth exploring in this context. We also plan to study the mathematical properties of the bounded biharmonic weights to determine the necessary conditions for which the observed locality and maximum principle hold.
Acknowledgments
We are grateful to Jaakko Lehtinen, Bob Sumner, and Denis Zorin for illuminating discussions, Scott Schaefer for the Gingerman and Pisa images, and Yang Song for helping implement the rigidity brush and 2D remeshing. This work was supported in part by NSF award IIS-0905502, ERC grant iModel (StG-2012–306877), SNF award 200021_137879, an Intel Doctoral Fellowship, and a gift from Adobe Systems.
Figures
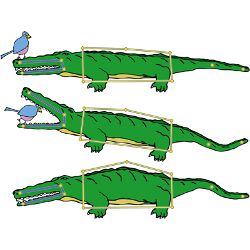
Figure 1. Our deformation method supports arbitrary combinations of control handles, such as points, bones, or cages. This versatility allows choosing the right tool: bones control rigid parts, cages reshape areas, and points transform flexible parts. Influence weights for each handle are precomputed at bind time, so high-quality deformations can be computed in real time with low CPU usage. Throughout the paper, colored frames illustrate linear transformations specified at point handles.
Figure 2. Different user control structures are appropriate for some situations and inappropriate for others. Setting up an enclosing cage can be both tedious and unintuitive: weaving around the Pirahna‘s teeth. A cage is necessary for precise articulation of the Vacuum, where scaling at points would be too crude. Points provide loose and smooth control of the Worm, but a skeleton deformation is too rigid and overly complex.
Figure 3. Deformation of the leaning tower (original is shown left). Cages provide more exact control over area than other handle types.
Figure 4. Bounded biharmonic weights are smooth and local: the blending weight intensity for each handle is shown in red with white isolines. Each handle has the maximum effect on its immediate region, and its influence disappears in distant parts of the object.
Figure 5. Weights must be smooth everywhere, especially at internal handles, which are likely to correspond to important features. Weights that have discontinuities at handles, like harmonic coordinates (center), introduce tearing artifacts with even slight transformations of the handles. Our weights are smooth, as shown on the right.
Figure 6. The generality of our optimization framework makes it possible to compute weights that respect salient object features. Marking a region preserves the shape of an eye (middle), which would otherwise be distorted (right).
Figure 7. The human skeleton embedded in the Armadillo does not control the tail or the ears, but points are easily added for additional expressiveness in each pose. Left: a cutaway of the Armadillo shows the graded tet mesh produced by TetGen. The inner tetrahedra are much larger than those near the surface. This keeps the discretization complexity reasonable.
Figure 8. Dropping the partition of unity constraint (5) greatly optimizes the precomputation of our weights without losing quality. Left: the mean absolute difference between the original and faster weights at each vertex, over all handle weights at that vertex. Deformations with the same handle configuration using our original (middle) and faster (right) weights are visually indistinguishable.
Figure 9. The Gargoyle is deformed using an internal skeleton and point handles.
Figure 10. Points articulate the flexible Octopus.
Figure 11. Fifty point handles (black and yellow) are randomly placed in a square domain. Left: the sign for the black handle’s unconstrained biharmonic weight (red for positive and blue for negative regions). The local maxima and minima are shown as red and blue dots, respectively. Right: the support regions for bounded biharmonic weights of the black handles. In this and all other tests, the weights are local. Here, there are no spurious local maxima.
Figure 12. Point handles deform the image by blending the affine transformations specified at each point. The cage on the boundary maintains the rectangular image shape or allows its resizing.
Figure 13. Cages that fully envelop 3D objects such as the Hand are difficult to set up. Skeletons are often easier to embed and manipulate. When cages are needed for precise volume control, our scheme makes them easier to use by allowing partial cages that only overlap parts of the object.
Figure 14. We show the trade-off between locality and linear precision within a cage. The rest pose of an image of text (a) is stretched horizontally by using harmonic coordinates (b1), and our bounded biharmonic weights (c1). Harmonic coordinates’ response is more global (b2) than ours (c2). On the other hand, HC maintains the vertical lines in letter T near the deformed handles (b3), while our weights reveal their lack of linear precision (c3).
Tables
Table 1. A summary of the properties of six methods for choosing blending weights. Our method often satisfies all necessary properties. We have empirical evidence but no formal proof for locality and sparsity; our weights often have no local maxima.
Table 2. Statistics for the various examples in the paper. |S| is the number of triangles of the input 3D model, |Ω| is the number of elements in the discretization of Ω, BT/h is the bind time per handle in seconds. Emean and Emax are, respectively, the mean and max absolute difference between our original weights with (5) enforced explicitly and our faster weights where each handle’s weights are solved independently and then normalized. Mean and max values are taken over both handles and vertices.
Join the Discussion (0)
Become a Member or Sign In to Post a Comment