The theme is Venn diagrams, those ubiquitous but useful pictures, usually consisting of two or three intersecting circles that illustrate how sets meet.
Venn diagrams were devised and introduced in 1880 by John Venn (18341923), Master of Arts, Fellow, and Lecturer in Moral Science, Caius College, Cambridge University, in a paper entitled “On the Diagrammatic and Mechanical Representation of Propositions and Reasonings.” To be precise, a Venn diagram of order n is a collection of n simple closed curves in the plane with the property that for each subset of the curves, there is exactly one component of the plane minus the union of the curves whose points lie inside the curves in the subset and outside the rest of the curves. The Venn diagrams considered here have the additional requirement that they are “simple,” meaning all intersections of curves are simple crossings involving just two curves.
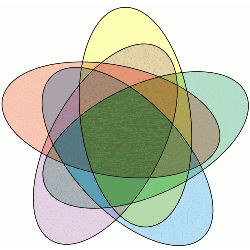
Pictured in the figure here is an order-5 Venn diagram consisting of five congruent ellipses, due to Branko Grünbaum of the University of Washington, Seattle. Curiously, Venn himself did not believe such a construction was possible.
Venn diagrams are very special figures of which much can be said. Here are two puzzles based on properties of Venn diagrams, and a third concerning a property Venn diagrams may or may not have:
- Prove that Venn diagrams of all orders exist; that is, construct for each n a Venn diagram of order n.
- Show that every Venn diagram of order n has the same number of vertices (crossing points); how many?
- Prove or disprove that to any Venn diagram of order n another curve can be added, making it a Venn diagram of order n+1; remember, only simple crossings allowed.




Join the Discussion (0)
Become a Member or Sign In to Post a Comment