Puzzled: Rectangles Galore

Welcome to three new puzzles. Solutions to the first two will be published next month; the third is (as yet) unsolved. In each, the issue is how your intuition matches up with the mathematics.

By Peter Winkler

Posted Nov 1 2010

Packing rectangles with six given dots at their lower-left-hand corners.

The hero of this column is the simple, ordinary, axis-aligned rectangle. Looking out the window, how many do you see? My view at the moment of Cambridge, MA, easily takes in more than one thousand, mostly windows. Asking new questions about an old figure helps us see it in a new light.

A large rectangle in the plane is partitioned into a finite number of smaller rectangles, each with either integer width or integer height; that is, its width, height, or both width and height are whole numbers of units. Now prove that the large rectangle, likewise, has integer width or height (or both).
You are in a large rectangular room with mirrored walls. Your mortal enemy, armed with a laser gun, is elsewhere in the room. As your only defense, you may summon a number of graduate students to stand at designated spots in the room, blocking all possible shots by the enemy. How many students do you need?
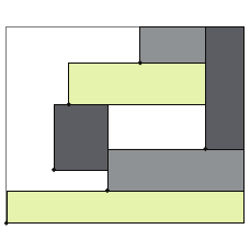
You may assume for this purpose that you, your enemy, and the students are all slim enough to be considered points (viewed from above), rather than solid figures in 3D space. If, for example, you had continuum many graduate students, you could place them around you in a circle, with the enemy outside. But you can do better…
Before you (on the plane) is a large rectangle containing a finite number of distinct dots, one of which is at the rectangle’s lower-left-hand corner. Your objective is to pack smaller, disjoint rectangles into the big one (with sides parallel to those of the big one) in such a way that each small rectangle includes one of the dots as its own lower-left-hand corner; see the figure for an example.

The conjecture is that there is always a way to choose the small rectangles so they cover at least half the area of the big rectangle. Be the first ever to prove it. A far as I know, no one has succeeded in even showing you can cover any fixed fraction (say, 1/100) of the area of the original rectangle.

Alternatively, if you reject the conjecture, find a counterexample, a way to distribute the dots (be sure to include the lower-left-hand corner of the big rectangle) so there is, provably, no way to do the packing so as to cover half the area of the big rectangle.