Quantum computing, which promises to harness the special properties of quantum mechanics to dramatically speed up calculations and thus help solve currently intractable problems, has attracted considerable investment from tech giants like Google, Microsoft, and IBM. Yet there is still no commercially available quantum computer because of the immense challenges in creating and running such a machine.
One of the major challenges is heat management. As with classical computing, quantum computing uses physical hardware and, therefore, is subject to the laws of physics, particularly the thermodynamics of computation. However, quantum computers are far more fragile than classical computers, requiring far lower temperatures to work properly. Also, as shown in a theoretical paper published in October 2020, the thermodynamics of quantum information processing can create highly unusual and potentially damaging effects for these delicate machines.
The paper, describing a study by researchers at the U.K.’s University of Manchester and Trinity College Dublin, models mathematically what happens when information gets erased in a quantum regime. All erasures cause some heat dissipation, as expected—but to their surprise, the researchers found that every once in a while, the heat dissipated from an erasure is extremely high. In uncovering the potential for such rare but high-impact events, the study suggested something about the future of quantum computing hardware: that it may have to use reversible logic, which by definition does not require erasure of information.
The research also brought back to the fore a famous paradox in thermodynamics that has intrigued scientists since the 19th century—and also a 20th-century insight into the relationship between information and heat, which not only resolved that paradox, but also has practical implications today.

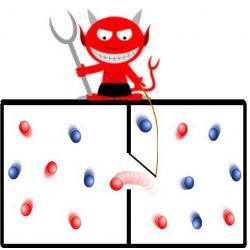
Figure. A bit of information can be encoded in the position of a particle (left or right). A demon can erase a classical bit (blue) by raising the left side until the particle is definitely on the right. A quantum particle (red) also can tunnel under the barrier, which generates more heat.
A Famous Paradox
The paradox, laid out by physicist James Clerk Maxwell, appeared to show a violation of the Second Law of Thermodynamics, which states that the entropy of a closed system is always increasing. Physicists of Maxwell’s day already knew the Second Law: they understood heat cannot spontaneously flow from a cold region to a hot one, any more than a cooked egg can return to a raw state. Yet Maxwell, writing to a colleague in 1867, described a hypothetical scenario in which this fundamental law did not seem to hold.
In Maxwell’s thought-experiment, a vessel was separated into two halves by a diaphragm, each half containing gas molecules moving at varying speeds; an intelligent being—later called “Maxwell’s demon” by Lord Kelvin—seeing the paths and velocities of all the molecules, selectively opened and closed a door in the diaphragm to let slow (cold) molecules move through to one side, and the faster (hotter) ones gather on the other side.
The result of this selection process: instead of the vessel reaching thermal equilibrium, “The hot system has got hotter and the cold colder and yet no work has been done,” as Maxwell put it. “Only the intelligence of a very observant and neat-fingered being has been employed.” Entropy seemed to decrease on its own, an apparent contradiction of the Second Law that has fascinated scientists ever since.
Many brilliant minds have tried to resolve this paradox. In the 1920s, physicist Leo Szilard, devising a single-particle version of Maxwell’s demon that reduced the setup to a binary decision problem, suggested that what accounted for the unseen energy costs was the demon’s measurements (though Szilard turned out to be wrong about that). Later, Claude Shannon, the father of information theory, hinted at a possible connection between information and thermodynamics through his use of the term “entropy,” but the connection was merely metaphorical. “He used ‘entropy,’ but he was talking about information—bits—not energy,” explains Janet Anders, a theoretical physicist working in quantum information science at the U.K.’s University of Exeter.
Landauer and Logical Irreversibility
Though these and other scientists did not quite resolve the paradox, they planted the seeds for a set of ideas that eventually would. In a seminal 1961 paper produced as part of a large research program at IBM to understand the physics of computation, Rolf Landauer put forth the erasure principle that now bears his name. Landauer’s principle, now considered the basic principle of the thermodynamics of information processing, states that erasing information always dissipates energy.
Destruction of information through erasure, analogous to irreversible processes in thermodynamics (like cooking an egg or letting a hot liquid reach room temperature), is what Landauer termed “logically irreversible.”
This means that once you’ve turned a series of 1s and 0s into all zeroes, which is what erasure accomplishes, you cannot know which state these bits were in before. (In this way, erasure is fundamentally different from a logically reversible process like swapping every 0 for a 1 and vice versa.) What’s more, Landauer argued, the logical irreversibility of erasure entailed physical irreversibility as well, because information is always represented on physical devices. “Whether that’s an abacus, or information written on a page, or electronics in a transistor; ultimately, the abstract notion of information is always encoded on physical hardware,” says physicist John Goold of Trinity College Dublin, one of the investigators on the quantum fluctuations study.
Or, as Landauer himself has put it, “Information is physical.”
One upshot of Landauer’s principle is that erasure of even one bit of information cannot be done for free; it always increases entropy. This minimum amount of heat released into the environment (a computable amount known as Landauer’s limit) is not only a fundamental limit on the efficiency of any irreversible computer; it is also a way to tackle Maxwell’s demon. As Landauer’s IBM colleague Charles Bennett would later explain, unless the demon has an infinite memory, making the observations necessary to separate hot from cold particles requires erasing bits of memory, something Landauer showed can’t be done without expending energy and thus increasing entropy.
Destruction of information through erasure, analogous to irreversible processes in thermodynamics, is what Landauer termed “logically irreversible.”
Besides helping resolve the famous paradox, Landauer’s ideas finally related information theory to thermodynamics. The ideas also reconciled another duality: an identity crisis within the emerging field of computer science. In an era when very few universities were offering degrees in computer science, “Computer scientists were really debating this question of what is this field about,” says Aaron Wright, a historian of science at Dalhousie University in Canada who has studied IBM’s research program on the physics of forgetting. “One of the big dividing lines was: is [the field] about machinery, or is it about mathematics? Landauer’s work blurred that distinction, Wright says: “Landauer’s principle is precisely connecting those two ostensibly separate worlds.” Thanks to Landauer, it is no longer a category error to ask, for example, “how much space does the Pythagorean Theorem take up?”
Engineering Implications
On a practical level, though, Landauer’s ideas have not had implications for engineers until recently. “Nobody designing a classical computer has had to worry about Landauer’s principle,” says Christopher Jarzynski, a physicist at the University of Maryland whose expertise includes the thermodynamics of small systems. “When we’re erasing information in our computers, we’re actually dissipating way more energy than Landauer’s limit.” That’s certainly a waste of energy, but with proper cooling, the dissipated heat poses no threat to the computer’s accuracy—and even if it did, it wouldn’t be because of proximity to Landauer’s limit.
With quantum computers, though, Landauer’s principle will become more relevant, and the paper by Goold and his colleagues clearly shows why. Even in classical mechanics, Goold explains, a key feature of the thermodynamics of microscopic systems—whether these small-scale systems are protein molecules or single-atom transistors—is fluctuation. In other words, “I have to perform the experiment many, many times, and I get different outcomes.” (In fact, because it takes a full probability distribution to show all these possible quantities of heat and work, another term for the thermodynamics of small systems is “stochastic thermodynamics.”) Microscopic particles obey the laws of thermodynamics on average, but dissipation events fluctuate greatly. At one extreme, some individual events can even appear to violate the Second Law.
This much has been known for years—but Goold and his colleagues wanted to understand some of the stochastic thermodynamics of quantum systems. So, using equations that model such things, they looked at erasing a bit of information in a quantum mechanical way. “We found that if you look at the fluctuations”—rare events—”you get very large, rare deviations when you get a quantum mechanical superposition,” Goold says. Since superposition (or the appearance of a particle in two positions simultaneously) is crucial to the way quantum computers do their magic, any extreme event that interferes with this behavior could be disastrous.
“In quantum computing, everyone is working on limiting errors because it’s already error-prone,” says Anders, the University of Exeter physicist, “so when you put in heat, you raise the chance of errors much more.” That’s why quantum computers must operate at extremely cold temperatures—which means, as Anders puts it, not just “you-have-to-put-your-socks-on cold,” but close to absolute zero.
What the study suggests to her is that in quantum computing, “you don’t want to do Landauer erasure, since that creates high heat events.” The alternative: “Whenever possible, you want to do reversible operations, so nothing is erased.”
Landauer, R.
Irreversibility and Heat Generation in the Computing Process IBM Journal, July 1961 https://www.informationphilosopher.com/solutions/scientists/landauer/Landauer-1961.pdf
Maddox, J.
Maxwell’s demon: Slamming the door. Nature 417, 903 (2002). https://doi.org/10.1038/417903a
Miller, H.J.D., Guarnieri, G., Mitchison, M.T., and Goold, J.
Quantum Fluctuations Hinder Finite-Time Information Erasure near the Landauer Limit Phys. Rev. Lett. 125, 160602 – Published 15 October 2020 https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.125.160602
Rex, A.
Maxwell’s Demon—A Historical Review Entropy 2017, 19(6), 240 https://www.mdpi.com/1099-4300/19/6/240/htm
Szilard, L.
On The Decrease Of Entropy In A Thermodynamic System By The Intervention Of Intelligent Beings English translation of the classical paper ober die Enfropieuerminderung in einem thermodynamischen System bei Eingrifen intelligenter Wesen, which appeared in the Zeitschrift fur Physik, 1929,53,840–856. http://fab.cba.mit.edu/classes/863.18/notes/computation/Szilard-1929.pdf
Wright, A.S.
The Physics of Forgetting: Thermodynamics of Information at IBM 1959–1982 Perspectives on Science 2016, vol. 24, no. 1 https://www.mitpressjournals.org/doi/pdf/10.1162/POSC_a_00194




Join the Discussion (0)
Become a Member or Sign In to Post a Comment