Recent Advances on Principles of Concurrent Data Structures

Our research group at the Instituto de Matemáticas of the Universidad Nacional Autónoma de México focuses in studying the principles underlying distributed computing, which covers a wide range of services in our everyday life, for example, cloud storage, cryptocurrencies, collaborative editing, as well as concurrent software that governs modern multicore computers. The goal of our discussion here is to survey our recent advances on one of our research lines: concurrent data structures. This type of data structures has attracted a great deal of interest as they are a key factor to exploit the inherent parallelism in modern multicore architectures, ubiquitous since the beginning of this century (see for example Herlihy¹⁰ and Shavit¹²).

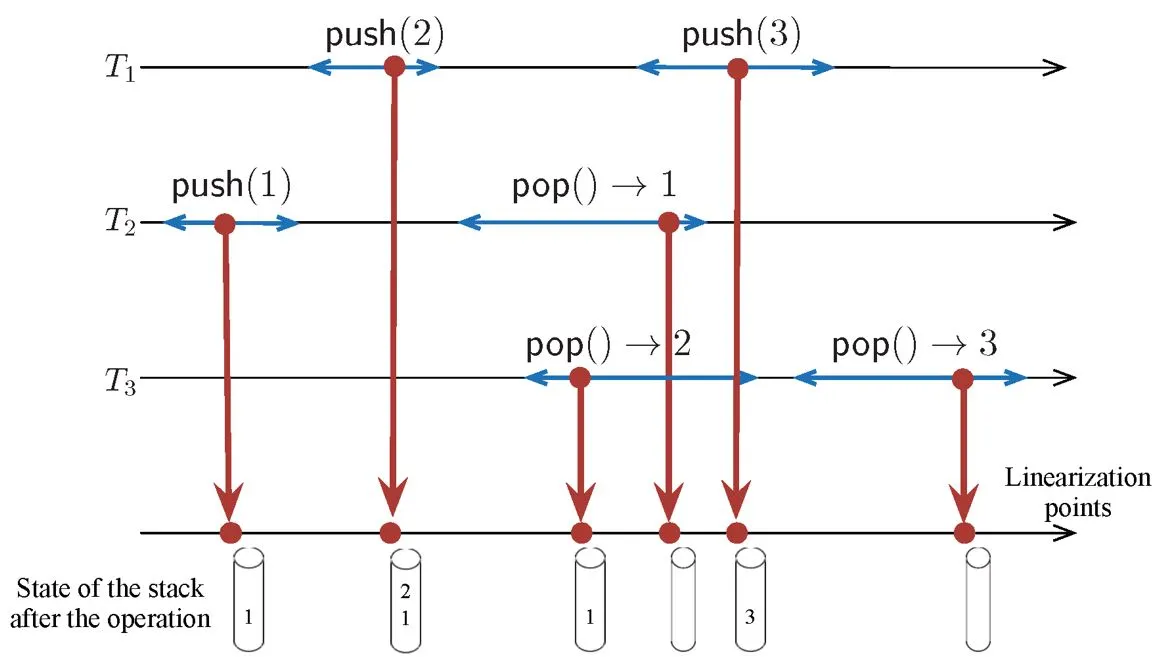
In a concurrent implementation of a data structure, a pool of threads modify the contents of the structure at unpredictable times, since they run asynchronously, through the operations provided by the data structure. Furthermore, the operations of different threads might overlap in time, because the threads themselves need to implement the data structure using the underlying coordination primitives provided by the operating systems, such as read/write on shared registers, compare set, and others. See Figure 1 for an example of an execution of a concurrent stack with three threads.

How do we know that a concurrent implementation of a stack is correct? What do we even mean by a “concurrent stack?” What do we mean by a “queue” if several threads can enqueue an item concurrently? In the classic case of sequential implementations there is a unique, “natural” definition of a data structure such as a queue or a stack. In contrast, in the concurrent world, this is not always the case, one can define correctness of concurrent implementations in several different ways, each of them useful in different applications.

The gold standard of correctness condition for concurrent implementations is linearizability.¹¹ Linearizability states that every operation appears as if it takes effect “instantaneously” at a unique point in time between its invocation and response. These sequence of linearization points induce a sequential execution of the operations, and the execution is correct, or linearizable, if there are linearization points that induce a sequential execution that satisfies the sequential specification of the object implemented. Figure 1 shows linearization points that induce a valid stack sequential execution.

Linearizability is so popular because of its practical usefulness and its theoretical properties. From the practical side, for example, it allows the design of concurrent software in a modular manner, which is key for the design and implementation of large-scale systems. Namely, if one designs independently two linearizable objects, it is guaranteed a system that uses both is also linearizable.

Despite all its benefits, after years of research, it is now well understood that linearizability has some inherent limitations. We provide two examples. There are concurrent data structures that cannot be analyzed through linearizability, since they do not have a sequential specification. For example, the exchanger object in the concurrent package of Java, which serves as a synchronization point where threads exchange items concurrently, has no sequential specification, because in sequential executions no exchanges take place. A second example is that it has been formally shown that some common data structures, such as sets, queues, stacks, and work-stealing for dynamic load balancing, only admit linearizable implementations that are inherently slow, for example Attiya et al.¹

In the past few years, part of the research in our group has been devoted to developing techniques to overcome the limitations of linearizability. We proposed an extension of linearizability, called interval-linearizability, that is expressive enough to specify data structures that are impossible to specify with linearizability^5,6 (such as the exchanger object); hence one can, for the first time, formally reason about correctness for them. These types of structures are “truly” concurrent, which is forbidden in linearizable specifications and implementations.

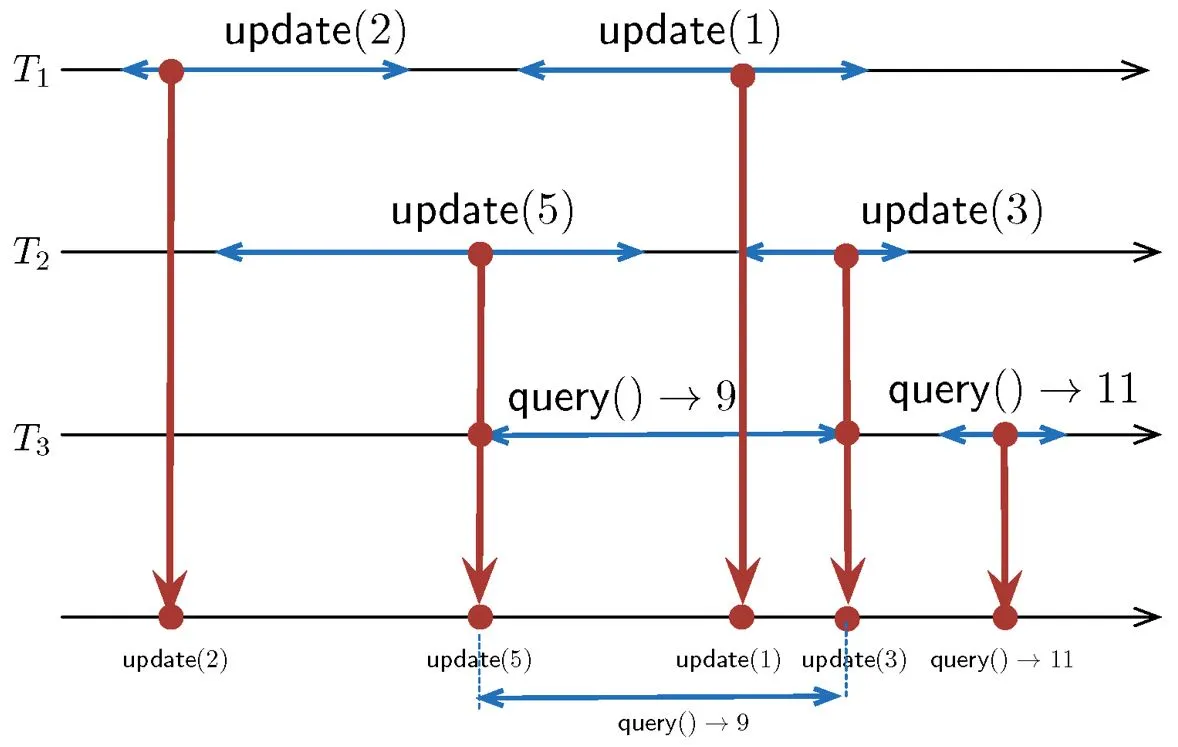
Generally, in an interval-linearizable implementation, every operation takes effect “continuously” in an interval of time, instead of instantaneously at a single point. During the interval, the operation might affect, or be affected by, the other operations whose linearization intervals it overlaps with, which is the mechanism that allows truly concurrent behaviors to be specified. Figure 2 depicts an example of an execution of a counter with an interval-linearizable query operation. Thus, linearizability is nothing else than interval-linearizability when all intervals are just points.

The interval-linearizability condition allowed us to formally specify new relaxed variants of classic data structures, such as queues and stacks and work-stealing, and provide simple and efficient implementations,⁷ some of them delivering a good performance when combined with solutions to practical parallel problems.⁴

A challenging task by itself is that of proving linearizability of an implementation, due to the large number of possible executions implementations can exhibit (it has been formally shown that deciding if a finite execution is linearizable is NP-complete, for some concurrent objects⁹). The formal verification community has provided different techniques to tackle this problem, each of them providing different levels of guarantees. Despite all efforts, proving linearizability remains challenging. Our group has explored new static and dynamic techniques that help with this task. We have proposed new static techniques for modular formal verification of concurrent implementations,³ as well as dynamic verification algorithmic approaches^2,8 that test at runtime whether the current execution of an implementation is linearizable, and possibly prevent side effects in case of non-linearizable executions.