
1. Invention in the 16th century
The sector and the related proportional compasses (proportional dividers) were developed in the second half of the 16th century. There are several inventors, most of them from Italy. Galileo Galilei improved the sector, Jost Bürgi the proportional compasses. The sector was in use until the end of the 19th century, the proportional compasses were utilized until the second half of the 20th century, partly even until today. The two mathematical instruments were widespread.
2. What is a sector?
The sector consists of two arms connected by a pivot joint (see Fig. 1). For example, linear, trigonometric, and logarithmic scales were engraved to the two bars. There were scales for circles, areas (square numbers), and volume (cubic numbers). They have Latin, English, or French names, e.g. linea arithmetica (linear scale), linea geometrica (square root scale), linea stereometrica (cubic root scale), linea astronomica or linea chordarum (trigonometric scale). There were Italian, French and English-style models. For calculations, dividers are required.
|
|
Fig. 1: Sector.
In contrast to the proportional compasses, sectors have a fixed hinge.
© ETH Library, Zürich, Collection of astronomical instruments
The linear scales of the two arms are used for each of the four basic arithmetic operations. They comprise 200 equal parts (called “lines”). Other scales are labeled with “planes,” “polygons,” “chords” (angles), etc. Sectors form similar triangles.
The pair of dividers is used to select a given distance on one of the two linear scales (from the zero point). The length of this straight line defines the distance between two equal numerical values on both linear scales. With the pair of dividers, you measure the distance between two equal marks (e.g. number 80 each) of the two linear scales. This distance is transferred to one of the two arms, where the result can be read.
Additions and subtractions take place as on normal (linear) scales. For these operations, the linear scales of the sector are used. For additions, two distances are joined together; for subtractions, one distance is subtracted from the other.
Digital machines count, analog devices measure. Since distances are measured with the sector, it is an analog instrument.
For multiplication and division, both the linear scales and the distances between the arms are used.
3. How do you multiply with a sector?
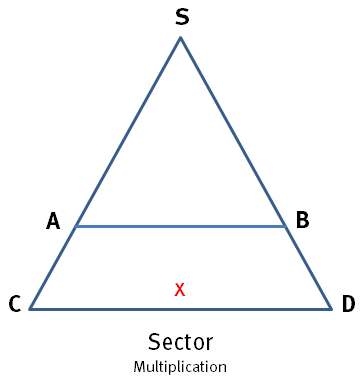
Example: 7 ⋅ 3 = ? (see Fig. 2)
- Select the value 7 (multiplicand) with the pair of dividers on one of the two linear scales.
- Open the two arms of the sector so far that the pair of dividers fits exactly between the values 10 of the two linear scales (value 10 = suitable, freely selectable number): distance AB (7).
- Use the pair of dividers to measure the distance between the two values 30 of the linear scales (value 30 = 3 ⋅ 10; 3 = multiplier): distance CD (21).
- Transfer this distance with the pair of dividers (from zero) to one of the two linear scales.
- Read the result (21).
SA : SC = AB : CD
10 : 30 = 7 : x
x = (7 ⋅ 30)∕10 = 21
10 : 30 = 7 : 21
Product: 21
SA : SC = AB : x
x = (AB ⋅ SC) / SA
Fig. 2: Sector (multiplication).
Thanks to the intercept theorem, it is possible to multiply on the sector. The product (x) corresponds to the distance CD.
© Bruderer Informatik, CH-9401 Rorschach
4. How do you divide with a sector?
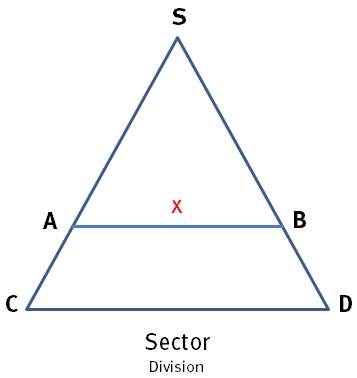
Example: 21 : 3 =? (see Fig. 3)
- Select the value 21 (dividend) with the pair of dividers on one of the two linear scales.
- Open the two arms of the sector so that the pair of dividers fits exactly between the values 30 of the two linear scales (value 30 = suitable, freely selectable number): distance CD (21).
- Use the pair of dividers to measure the distance between the two values 10 of the linear scales (value 10 = 30/3; 3 = divisor): distance AB (7).
- Transfer this distance with the pair of dividers (from zero) to one of the two linear scales.
- Read the result (7).
SC : SA = CD : AB
30 : 10 = 21 : x
x = (21 ⋅ 10)∕30 = 7
30 : 10 = 21 : 7
Quotient: 7
SC : SA = CD : x
x = (CD ⋅ SA) / SC
Fig. 3: Sector (division).
Thanks to the intercept theorem it is possible to divide on the sector. The quotient (x) corresponds to the distance AB.
© Bruderer Informatik, CH-9401 Rorschach
6. Concluding remarks
Many people find arithmetic difficult. Therefore, for thousands of years, attempts have been made to facilitate this work with technical aids. However, the path from finger reckoning via the (digital) abacus, the (analog) sector, the (analog) slide rule and the (digital) mechanical calculating machine to today’s electronic computer was long and stony.
References
You can find detailed information on the sector and the proportional compasses as well as step-by-step instructions in:
- Herbert Bruderer: Meilensteine der Rechentechnik, De Gruyter Oldenbourg, Berlin/Boston, 2. völlig überarbeitete und stark erweiterte Auflage 2018, 2 Bände, 1600 Seiten
- Herbert Bruderer: Milestones in Analog and Digital Computing, Springer Nature Switzerland AG, Cham, 3rd, revised and extended edition 2020, 2 volumes, about 2000 pages
Herbert Bruderer is a retired lecturer in didactics of computer science at ETH Zürich. More recently, he has been an historian of technology. bruderer@retired.ethz.ch, herbert.bruderer@bluewin.ch



Join the Discussion (0)
Become a Member or Sign In to Post a Comment