
- because of the deep ideas and questions in computing that are important to know,
- because of the things you can build,
- because of the unique things you can express with computing, and
- as a tool for exploring ideas and data.
First a brief lesson: Digital sounds are made up of samples, essentially, measures of air pressure on a microphone at moments in time. For CD-quality sound, these samples are collected 44,100 times per second. These samples typically have integer values varying between -32768 and 32767 because we typically collect 16 bit samples.
First time I ever taught MediaComp, and I taught the above facts, someone asked from the back of the room, “What if you set all the samples to 32767?!? Would your speakers explode?” Try it — you hear nothing at all, except for maybe some speaker hum. Human hearing is based on changes in sound pressures. Having constant higher pressure isn’t sound.
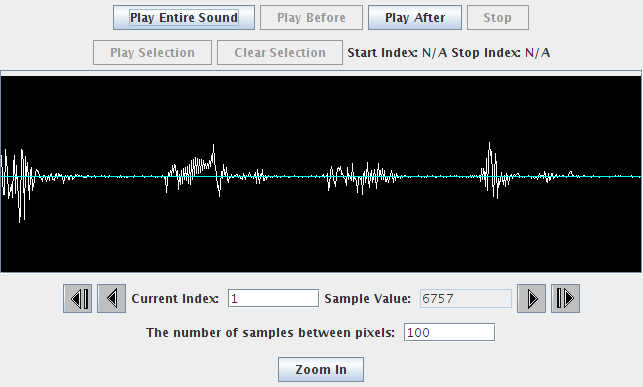
But, I offered him an alternative that gets to what he really wanted to do. I opened a sound of me saying “This is a test.” (Click on that link to hear the sound.) Here’s what the visualization of the sound looks like in the Sound Explorer in our Python IDE, JES.
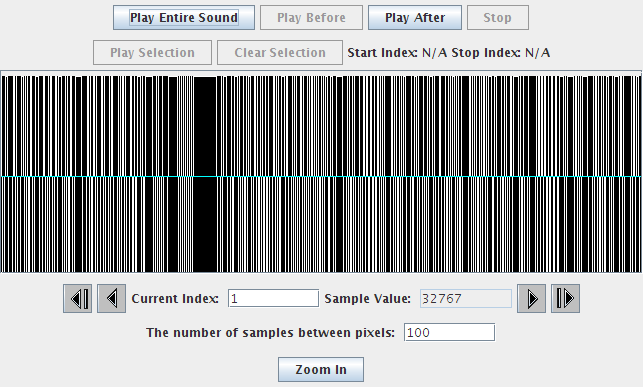
I then wrote a program to change the value of each sample. If it’s at positive, make it as positive as it can possibly be. If it’s not or zero, make it as negative as it can possibly be.
def maximize(sound):
for sample in getSamples(sound):
value = getSampleValue(sample)
if value setSampleValue(sample,-32768)
if value > 0:
setSampleValue(sample,32768)
The new sound visualization looks like this:
Were you surprised? While it is very noisy (try to work out why), we can make out the words. Why? Usually someone in the class figures out that we have not changed the frequency of the sound. We’ve changed the amplitude of the sound, but the number of zero crossings and where they are (in time) has not changed at all. That tells us that human understanding of speech is much more dependent on sound frequency than amplitude and thus volume.
There’s an interesting computer science implication here, too. How many bits are necessary to record speech, per sample? In this experiment, we’re showing that the answer is “one.” We have re-encoded the sound into either high amplitude or low amplitude, 1 or 0. And we can hear the speech. What are all the bits (16 typically) that we normally use for encoding sound really representing? There’s a question for another class.



Join the Discussion (0)
Become a Member or Sign In to Post a Comment