

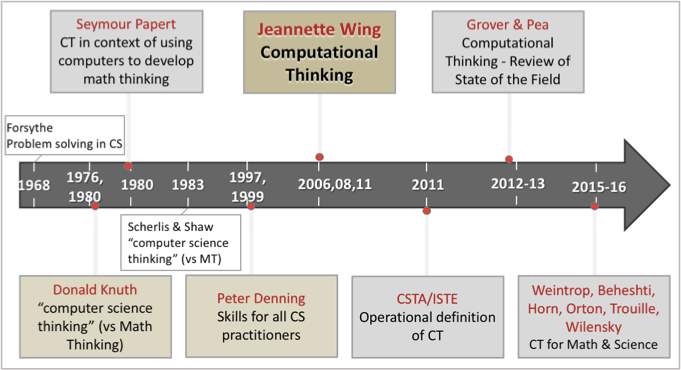
Last week, Fred Martin (current chair of the CSTA Board and my co-conspirator on the “CT From K-12 Disciplinary Perspectives” NSF-funded effort), while speaking at a CSTA meeting in New England, presented a broadly accepted timeline of Computational Thinking (CT).
Although Jeannette Wing should undoubtedly be credited for taking the CT phrase and idea mainstream in 2006, it’s time we revised the timeline to recognize several computer scientists for articulating elements of “computer science thinking” and CS practices well ahead of Wing’s writings on ‘thinking like a computer scientist’. Two noteworthy articles are discussed below.
It’s also clear to me that in order to help make better sense of CT, we must acknowledge and distinguish two views of CT for K-12 education that are defined and operationalized based on the context for teaching/learning/application. One is a view of CT as a thinking skill for CS classrooms, that includes programming and other CS practices with the goal of highlighting authentic disciplinary practices and higher-order thinking skills used in computer science. The other is CT as a thinking skill/problem-solving approach in non-CS settings—this is often about using programming to automate abstractions of phenomena in other domains or work with data with the goal of better understanding phenomena (including making predictions and understanding potential consequences of actions), innovating with computational representations, designing solutions that leverage computational power/tools, and engaging in sense making around data.
View 1: CT as ‘Computer Science Thinking’ in CS classrooms
Although problem solving practices of CS were discussed as early as 1968 (by G.E. Forsythe), amongst the earliest articles to articulate elements of CS thinking was Algorithms in Modern Mathematics and Computer Science by Donald Knuth (circa 1980), in which he wrestles with the question, “Do most mathematicians have an essentially different thinking process from that of most computer scientists?” Interestingly, he refers to the thinking processes of computer scientists as “computer science thinking.” (It is worth noting that Knuth essentially equated CS to “primarily the study of algorithms,” which was a popular view of CS at the time); and so in his view, “algorithmic thinking” = “computer science thinking” essentially. Knuth lists key elements of mathematical thinking (MT) and compares/contrasts them with elements of algorithmic/computer science thinking (CST). His list for CST overlaps with MT in the areas of formula manipulation, representation of reality*, reduction to simpler problems*, abstract reasoning*, information structures*, and algorithms* (where * indicates strong, as opposed to mild, connection). He also states that generalization and formula manipulation involve the general idea of pattern recognition. He highlights that unlike MT, CST does not deal with infinity, and conversely some kinds of CST are not part of MT: (1) dealing with complexity (MT does not care about efficiency/economy/cost of operations) and (2) the dynamic notion of “state” of a process (which includes the idea of variable “assignment”). It’s also fascinating that Knuth & Pardo expressed the notion of the assignment operator as a unique aspect of CST in an earlier 1976 article —”As we have remarked, mathematicians had never used such an operator before; in fact, the systematic use of assignments constitutes a distinct break between computer-science thinking and mathematical thinking.”
The second noteworthy article in my view, Computer Science: The Discipline, was written in 1997 (revised in 1999) by Peter Denning. In addition to discussing key content topics that comprise computing, Denning outlines “Standard Concerns of the Field,” and states that “every practitioner of the discipline must be skilled in four basic areas: algorithmic thinking, representation, programming, and design.” He goes on to explicate each of these as follows:
- Algorithmic thinking is an interpretation of the world in which a person understands and formulates actions in terms of step-by-step procedures that give unambiguous results when carried out by anyone (or by a suitable machine).
- Representation addresses the way in which data are stored so that the questions one will ask about them can be answered efficiently. The skill of representation goes beyond knowing how to organize data for efficient retrieval or processing. It deals with inventing ways of encoding phenomena to allow algorithmic processing
- Programming enables people to take algorithmic thinking and representations and embody them in software that will cause a machine to perform in a prescribed way. This skill includes working knowledge of different programming languages (each having its own strengths and limitations), program development tools (which aid testing, debugging, modularity, and compatibility), and operating systems (which control the internal operations of computers).
- Design connects the other three skills to the concerns of people, through the medium of systems that serve them. Design includes many practical considerations such as engineering tradeoffs, integrating available components, meeting time and cost constraints, and meeting safety and reliability requirements.
There’s a substantial overlap between CT elements defined in recent works (e.g., by Grover & Pea (2013), CT as defined by CAS, and the K-12 National CS Framework) and Denning’s 4 basic areas of CS “practice” (as well as Knuth’s elements of CST). Certainly, some elements of CT in recent descriptions (such as debugging, modularity, evaluation) have been called out separately as opposed to being encapsulated in other practices, but the basic idea of a set of CS problem-solving skills of which programming is but one is abundantly clear. To me, the separation of programming from algorithmic thinking, representation, and design is a direct answer to the question, (Is) CT == programming? As many of us have often reiterated, CT is more than programming. This, as we can see, is especially true in the CS context.
Though not neatly articulated by Wing, this view of CT helps focus on practices and deeper thinking skills even as we teach programming and CS topics. (This was central to my dissertation research). Knuth and Denning articulate this disciplinary thinking skill/practice of CS. As I wrote in a recent blog post, just as all STEM (and other) disciplines have been pushing toward privileging disciplinary ways of thinking in their K-12 curricula, so must CS push to focus on teaching disciplinary ways of thinking of CS—which is what Denning argued for all practitioners of CS to know, in addition to CS content knowledge.
View 2: CT in other disciplines.
The second view of CT sits squarely in the realm of “computational X,” i.e., integration of CT to enable/enrich learning in other disciplines, mainly through the vehicle of programming and automating abstractions and models in other disciplines. Papert’s use of Computational Thinking (in both Mindstorms and Situating Constructionism) was incidental and never explained. However, one can surmise from his writings that he meant ‘thinking with a computer’, or using the computer ‘as a tool to think with‘, to engage with topics/concepts in other disciplines. In fact, his book, and theses leading up to the book, were aimed largely at developing a ‘mathematical way of thinking (MWOT)’ and how children could use computers to develop MWOT (see Papert’s 1972 article Teaching children to be mathematicians versus teaching about mathematics). Denning’s recent writings on CT have highlighted that computational science has been the shining example and best argument for CT as a valuable way of bringing CS and computers into non-CS disciplines. I see diSessa’s idea of Computational literacy as closely aligned to this view.
Weintrop et al. (2016) operationalized this view of CT based on two decades of research (on computer-based systems modeling) led by Uri Wilensky and his research lab. Although I do believe that their framework is better suited to CT in science than CT in math or other subjects, it presents a way to frame CT for non-CS classrooms. It’s easy to see why this operationalization of CT might make sense to computational scientists. Here, CT operates somewhat differently than the elements of “computer science thinking” or CS practices outlined by Knuth, Denning (1997), Wing, Grover & Pea (2013)—it is driven by the need to marry representations and algorithms with concepts from the host domain (math or science or language arts or social studies), and programming these representations and algorithms provides a novel form of engagement with, and sense-making of, those concepts.
CT is a thus a thinking skill that has a place in both CS learning and learning other subjects. It can be learned in both settings, and it enriches learning in both settings. Teaching CT in both settings ensures deeper learning of CS disciplinary practices/skills (programming among others) in CS classrooms and bringing CS problem-solving approaches (representations/programming/computational modeling perhaps being the most valuable) to non-CS settings. Ideally, learners will get to experience CT in both types of settings, and in increasingly sophisticated ways, over the course of their K-12 journey.
Which brings me to the timeline. A historical timeline of CT should acknowledge Knuth and Denning (1997)’s contributions, for expounding on “computer science thinking” and “CS practices.” And so, here’s an attempt at creating a revised timeline that reflects the two views described above.
Where Wing Went Wrong
As Mark Guzdial recently observed in a tweet, there are few takers for Wing’s view of CT as an everyday skill. Everything about CT described above is about enriching CS learning and learning in other disciplines. Transfer between curricular contexts is hard enough. I think for now we can safely sidestep dreams of CT changing everyday behaviors of those who’ve learned this skill in curricular settings.
That said, I do believe that the field owes Wing a debt of gratitude for igniting K-12 CS education by re-surfacing such a thing as “thinking as a computer scientist” and for highlighting its relevance in other subjects as well. Yes, we are still working on operationalizing it for various grade levels and figuring out how to use this thinking skill to foster deeper learning in CS and non-CS classrooms, but questioning the existence of such a thing as ‘computational thinking’ is essentially questioning the very notion of ‘thinking like a computer scientist’.
What’s in a name?
So what about ‘Computational Thinking’ —the name Wing gave to ‘thinking like a computer scientist’? A few researchers have attempted to suggest/use alternatives. Even though personally I might prefer “computational problem solving” or even “computer science thinking” (now that ‘computer science’ as a K-12 subject has become a mainstream idea), I would argue against such renaming. Sure, there are avatars of CT—there’s computational fluency, an evolution of Mitch Resnick’s ‘Technological Fluency‘ idea (out of which Scratch was born) that appears to be CT with a heavy dose of creation (programming) and self-expression; computational doing or computational action (can there really be doing or action without thinking?), and computational participation (which is mostly about the social around programming). In recognition of socio-cultural theories of learning and Resnick’s work, the K-12 CS Framework, CAS, and Grover & Pea (2018) have broadened the scope of CT practices to include creativity and creation of computational artifacts; I believe this is especially helpful for K-12 ‘CS For All’. That said, a coding-heavy focus runs the danger of devolving into what Idit Harel calls “pop computing” (that mirrors my earlier warning).
At the recent ICLS symposium on assessment of CT at the Festival of Learning in London, all these views and avatars of CT were on full display, and it was heartening to see the packed room of researchers from around the world acknowledge and embrace them all. As the field of K-12 CS education evolves, I believe we can be open to all these variants co-existing under this broad umbrella of skills and practices inspired by computer science.
Shuchi Grover is a computer scientist and learning sciences researcher based in Palo Alto, CA. Her doctoral work at Stanford University and subsequent research has focused on K-12 computer science education, and especially computational thinking in CS and STEM+Computing integration settings at the primary and secondary school levels.



Join the Discussion (0)
Become a Member or Sign In to Post a Comment