Back in 1979, two scientists wrote a seminal textbook on computational complexity theory, describing how some problems are hard to solve. The known algorithms for handling them grow in complexity so fast that no computer can be guaranteed to solve even moderately sized problems in the lifetime of the universe. While most problems could be deemed either relatively easy or hard for a computer to solve, a few fell into a strange nether region where they could not be classified as either. The authors, Michael Garey and David S. Johnson, helpfully provided an appendix listing a dozen problems not known to fit into one category or the other.
“The very first one that’s listed is graph isomorphism,” says Lance Fortnow, chair of computer science at the Georgia Institute of Technology. In the decades since, most of the problems on that list were slotted into one of the two categories, but solving graph isomorphism—in essence figuring out if two graphs that look different are in fact the same—resisted categorization. “Graph isomorphism just didn’t fall.”
Now László Babai, a professor of computer science and mathematics at the University of Chicago, has developed a new algorithm for the problem that pushes it much closer to—but not all the way into—the easy category, a result complexity experts are hailing as a major theoretical achievement, although whether his work will have any practical effect is unclear.
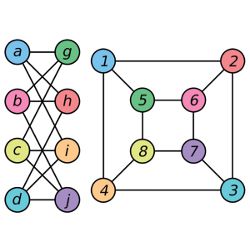
In computer science, a graph is a network, a series of nodes strung together by connections known as edges; the set of Facebook users and their interconnections make up a graph with approximately 1.5 billion nodes. Two graphs may be depicted differently, but if the nodes and connections in one match up with those in the other, they are equivalent—that is, isomorphic—graphs. Graph isomorphism can be used for applications as diverse as searching chemical databases or performing facial recognition; is that the same molecule or the same face, even though the atoms have been flipped or the smile has become a grimace? “Once you know two things are the same, then you can take what you know about one and apply it to the other,” Fortnow says.
Graph isomorphism is a subset of string isomorphism; in fact, string isomorphism is the subject of Babai’s paper, although it mainly discusses graphs. While there had been solutions for various special cases of graphs, “this works for everything,” says Fortnow, who describes Babai as having been his mentor when he started his career as an assistant professor at the University of Chicago.
What Babai’s solution does is check subsections of graphs for isomorphism through a variety of relatively simple means; for instance, by comparing how many neighbors each node has. Trouble arises if any of those subsections turn out to be Johnson graphs, which are so highly symmetrical, it can be difficult to tell if one is the same as another.
“Basically, what it boils down to is he shows that if this process gets stuck, there must be a Johnson graph hiding there,” Fortnow says. Having uncovered a hidden Johnson graph, Babai’s paper describes how to check that graph.
Babai first presented his results in a talk in November 2015, and in December published a paper on the open access website ArXiv. The paper has been accepted to the 48th ACM Symposium on Theory of Computing (STOC 2016). Babai declined an interview, saying the work needed to be vetted by other computer scientists. Fortnow says that, while it is a good idea to have many people look over such a complicated proof, the results are probably sound. “I think the rest of us really believe it’s either correct as is, or if there’s some problem, it can be easily fixed,” he says.
P or NP?
The difficulty with graph isomorphism has been figuring out what kind of problem it is. Many problems are considered “easy.” As they grow larger, the time it takes a computer to solve them increases no faster than a polynomial function of the problem’s size. The time needed to solve these P problems can grow large, but not unreasonably so. At the other end of the scale are problems in which the solution time of any known algorithm probably grows exponentially with the size of the problem, to the point where it becomes unfeasible for the computer.
What Babai’s solution does is check subsections of graphs for isomorphism through a variety of relatively simple means.
The P problems that can be solved in polynomial time belong to a larger class known as NP. NP includes any problem in which, regardless of how difficult it is to solve, showing the solution is true is easy. The Traveling Salesman problem is a classic example; it asks for the shortest route that allows a traveling salesman to visit a list of cities once and return to the starting point. Coming up with that route is challenging, but once given the route, it can be easily checked.
Another subset of NP is NP-complete. No polynomial algorithm is known for any NP-complete problem, but if one were discovered, there would be an algorithm for all of them and the two classes, P and NP-complete, would collapse into one. Scientists do not know whether no efficient algorithm exists for solving NP-complete problems, or whether they have simply failed to find one yet. Since 2000, the Clay Mathematics Institute has offered a $1 million prize to anyone who can show whether P equals NP.
Babai’s work does not answer that question, but it still intrigues theoreticians. Graph isomorphism has never been shown to be in P, because there is as yet no known algorithm to solve it in polynomial time. On the other hand, there is evidence it is not NP-complete either. The best theoretical algorithm, published by Babai and Eugene Luks in 1983, was sub-exponential—better than any known algorithm for any NP-complete problem, but still far from easy. This new algorithm appears to place graph isomorphism in quasi-polynomial time, much closer to the easy side. “This is just such a huge theoretical improvement from what we had before,” Fortnow says. “Now it’s not likely at all to be NP-complete and it’s not that hard at all.”
Josh Grochow, an Omidyar Postdoctoral Fellow in theoretical computer science at the Santa Fe Institute in New Mexico, calls Babai’s proposed solution a big theoretical jump. “There really are very few problems we know of in this limbo state,” he says. Graph isomorphism is “still in the limbo state, but it’s a lot clearer where it sits.”
In some subset of graphs, the question was already settled. For instance, molecular graphs have “bounded valence,” meaning the physical constraints of three-dimensional space allow atoms to be connected only to a limited number of other atoms, says Jean-Loup Faulon, a synthetic biologist at the University of Manchester, England, and INRA in France, who uses graph matching in his work. In the 1980s, he points out, Babai, Luks, and Christoph Hoffmann showed bounded valence graphs could be solved in polynomial time. “Therefore, the problem of graph isomorphism is already known to be polynomial for chemicals,” Faulon says.
While Babai’s work has generated much excitement among theoreticians, experts say it is not likely to have much effect in practice; at least, not immediately. Scott Aaronson, a computer scientist at the Massachusetts Institute of Technology who studies computational theory, says, “this is obviously the greatest theoretical algorithms result” at least since 2002, when Manindra Agrawal, Neeraj Kayal, and Nitin Saxena came up with an algorithm for determining, in polynomial time, whether a number is a prime. “On the other hand,” Aaronson says, “the immediate practical impact on computing is zero, because we already had graph isomorphism algorithms that were extremely fast in practice for any graphs anyone would ever care about.”
In fact, the graph isomorphism solution is similar to the Agrawal-Kayal-Saxena algorithm in that way, says Boaz Barak, Gordon McKay professor of Computer Science at Harvard University’s John A. Paulson School of Engineering and Applied Sciences. “It was a great intellectual breakthrough, but even before it, we had highly efficient heuristics that seemed to solve the problem.” Barak says Babai’s paper contains several significant new ideas that may have an effect on mathematics and may someday lead to practical applications in graph isomorphism or some other problem, adding, “however, it is impossible, at least for me, to predict this potential impact at this point.”
Separate Spheres
Practical solutions for specific cases of graph isomorphism have existed for years. In a 1981 paper entitled “Practical Graph Isomorphism,” computer scientist Brendan McKay of the Australian National University in Canberra developed an isomorphism testing program called nauty (for No AUTomorphisms, Yes?) that is widely used today. He describes the difference between the theory and practice of graph isomorphism “as being like two galaxies that have only a few stars in common.” McKay does not believe this breakthrough will help close the gap between theory and practice, a belief he says he shares with Babai. “Nobody knows how to apply any of Babai’s ideas to improve the practical performance of programs for graph isomorphism,” McKay says. “If one just programs Babai’s algorithm on a computer without making any changes, it will be hopelessly slow compared to the best current programs.”
Faulon hopes Babai’s ideas do eventually lead to some changes in practice. “We are still lacking a practical polynomial-time algorithm in chemistry,” he says.
Another person hoping the theory can be translated into practice is Hasan Jamil, a computer scientist at the University of Idaho’s Institute for Bioinformatics and Evolutionary Studies. Jamil is searching for a gene that affects the death of cells in neurological disorders such as Alzheimer’s and Parkinson’s diseases. Graph matching for the cells’ regulatory networks and protein networks could help him isolate such a gene or set of genes. When he submitted a paper and the reviewers asked for a new experiment to back up his theory, however, the publication process slowed to a crawl. “If I have to find an isomorphic match, or even an approximate match, it takes hours and hours and months to even find simple things,” he says. With approximately 24,000 genes in the human body, each of them capable of producing four or five different proteins and then of interacting amongst themselves, the number of possible matches quickly becomes astronomical.
He hopes Babai’s proposed solution leads to something better. “If it brings down the complexity, even a bit, it helps us search things in a reasonable amount of time,” Jamil says.
If Babai’s work does lead to practical improvements, they may lie far in the future. McKay says, though, that Babai’s ideas have started him thinking about whether there might be some useful application. “The odds don’t look good,” McKay says, “but just maybe there is a pleasant surprise lurking.”
Further Reading
Babai, L.
Graph Isomorphism in Quasipolynomial Time, arXiv, Cornell University Library, 2015, http://arxiv.org/abs/1512.03547
McKay, B.D., and Piperno, A.
Practical Graph Isomorphism II, Journal of Symbolic Computation, 60, 2014, http://arxiv.org/abs/1301.1493
Fortnow, L.
The status of the P versus NP problem, Communications of the ACM, September 2009, http://cacm.acm.org/magazines/2009/9/38904-the-status-of-the-p-versus-np-problem/fulltext
Fortnow, L., and Grochow, J.A.
Complexity classes of equivalence problems revisited, Information and Computation, 209, 2011, http://arxiv.org/pdf/0907.4775.pdf
Isomorphic Graphs, Example 1, Stats-Lab Dublin https://www.youtube.com/watch?v=Xq8o-z1DsUA




Join the Discussion (0)
Become a Member or Sign In to Post a Comment