A group of people is sitting around your dinner table with one empty chair. Each person has a name that begins with a different letter: A, B, C … Because you love puzzles, you ask them to rearrange themselves to end up in alphabetical order in a clockwise fashion, with one empty chair just to the left of the person whose name begins with A. Each move involves one person from one chair to the empty chair k seats away in either direction. The goal is to minimize the number of such moves.
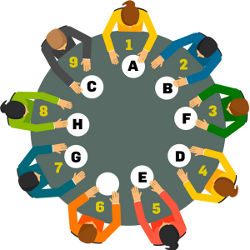
Warm-up. Suppose you start with eight people around the table, with nine chairs. The last name of each person begins with the letter shown, and you are allowed to move a person from one chair to an empty chair three chairs away in either direction (see Figure 1). Can you do it in four moves?
- Solution to Warm-Up
- C moves from 9 to 6
- F moves from 3 to 9
- C moves from 6 to 3
- F moves from 9 to 6
Now here is a more difficult version of the problem in which the only moves allowed are four seats away, starting with the configuration in Figure 2.
- Solution
- B moves from 6 to 2
- F moves from 1 to 6
- A moves from 5 to 1
- E moves from 9 to 5
Now try to solve these four related upstart puzzles:
Number of people n and move distance k. Given any number of people n and move distance k, find the minimum number of moves that would create a clockwise sorted order;
Number of people n in a certain arrangement, find best move distance. Given any number of people n, find a move distance k and the minimum number of moves of length k that creates a clockwise sorted order;
Number n of people, one empty chair. Generalize the problem with n people and one empty chair to allow movements of distances k1, k2, …, kj for some j < n/2; and
Several empty chairs. Generalize the problem further to allow several empty chairs.
Figures
 Figure 1. (warm-up). The goal is to rearrange the people around the table to be in clockwise alphabetical order, using as few moves as possible, where each move involves moving a person three seats away (in either direction) from the empty chair.
Figure 1. (warm-up). The goal is to rearrange the people around the table to be in clockwise alphabetical order, using as few moves as possible, where each move involves moving a person three seats away (in either direction) from the empty chair.
 Figure 2. The goal is again to rearrange the people around the table to be in clockwise alphabetical order, using as few moves as possible, where each move involves moving a person four seats away (in either direction) from the empty chair.
Figure 2. The goal is again to rearrange the people around the table to be in clockwise alphabetical order, using as few moves as possible, where each move involves moving a person four seats away (in either direction) from the empty chair.



Join the Discussion (0)
Become a Member or Sign In to Post a Comment